IRS多用户系统仿真结果及分析

2023-08-23 理论教育版权反馈

【摘要】：图7.11不同用户数下和速率随发射天线数M的变化曲线图7.11展示了不同用户数下，系统可实现和速率随基站的天线数M变化的近似结果及蒙特卡洛仿真结果。从式中不难发现，基站传输功率的提升同样会增大系统能耗，同样IRS元素个数和用户数均会对能耗产生影响。图7.15还反映出IRS元素个数的增多同样会造成损耗。

在本节中，验证了多用户场景中智能反射表面辅助的大规模MIMO下行链路可实现和速率以及能量效率的近似结果和蒙特卡洛结果。在仿真中，设置最大用户数K=5，用户坐标为{（340，201，0），（10，182，0），（397，90，0），（420，260，0），（310，302，0）}，且噪声功率为=-114dBm。基站的坐标为（0，0，40），IRS的坐标为（264，237，20）。根据文献[183]，选取IRS元素之间的间距为dIRS=0.03m。通过与[147]中类似的分析，将基站到IRS和IRS到用户之间的信道分别建模为，其中C0=-30dB，表示在参考距离dref=1m处的路径损耗；v=2.4，表示路径损耗指数；dB2I，l表示基站与第l块IRS之间的距离；dI2U，kl表示第k个用户与第l块IRS之间的距离。莱斯信道中的到达角和离开角均匀分布在区间上，并假设莱斯因子ξg，n=ξf，k=ξ。

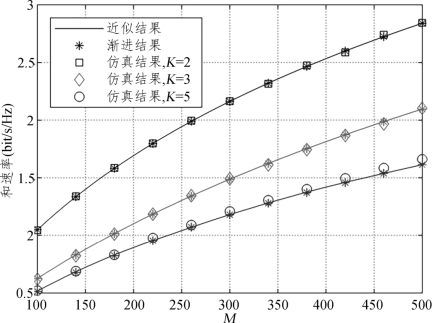
pagenumber_ebook=176,pagenumber_book=169

图7.11　不同用户数下和速率随发射天线数M的变化曲线

图7.11展示了不同用户数下，系统可实现和速率随基站的天线数M变化的近似结果及蒙特卡洛仿真结果。仿真中设置了基站总发射功率PT=15dBm，第k个用户传输信号的发射功率pk=PT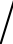 pagenumber_ebook=176,pagenumber_book=169 K，反射表面元素总个数N=300，第l块反射表面的元素个数为Nl=N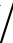K，莱斯因子ξ=15dB。图中实线所示的曲线对应于定理7.1中的结论即式（7.46），星号所示的曲线对应于推论7.1。图中的近似曲线与蒙特卡洛仿真曲线高度吻合，证明了结果的准确性，渐进曲线紧密贴合近似曲线证明了推论7.1的正确性。从图中可以看出，增大发射天线的数量可以有效地提高系统的可实现和速率。此外，用户数的增多会导致和速率的下降，这是由于用户数越多，每个用户可分配到的功率和反射表面元素个数就会越少，另外用户处接收到的信干噪比中的干扰会增强，因此使得可实现和速率的下降。

图7.12展示了不同用户数下，系统可实现和速率随智能反射表面元素个数的变化情况。仿真中设置基站总发射功率PT=25dBm，第k个用户传输信号的发射功率pk=PT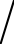 pagenumber_ebook=176,pagenumber_book=169 K，第l块反射表面的元素个数为Nl=N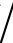K，莱斯因子ξ=15dB。图中表明了反射表面元素的增多可以有效提升可实现和速率。当用户数较多时，每个用户接收到的干扰信号也会相应较多。同时，图中表明了当IRS元素个数较少时，可以通过增加传输天线数来弥补。

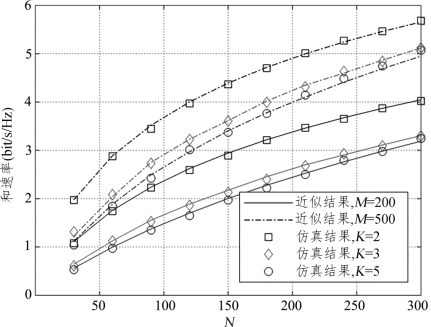
pagenumber_ebook=177,pagenumber_book=170

图7.12　不同用户数下和速率随智能反射表面元素个数N的变化曲线

信号传输功率同样是影响系统性能的重要因素，图7.13给出了不同用户数下，可实现和速率随基站总传输功率的近似结果、渐进结果以及蒙特卡洛仿真结果。仿真中设置了基站的传输天线数M=200，第k个用户传输信号的发射功率pk=PT pagenumber_ebook=177,pagenumber_book=170 K，发射表面元素总个数N=300，第l块反射表面的元素个数为Nl=N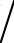K，莱斯因子ξ=15dB。从图中可以看出，可实现和速率不会随着传输功率的增大而无限增大，而是会达到一个上限，且该上限值与天线数、反射表面元素个数有关。这是由于增大信号的传输功率，不仅会增大有用信号的功率，还会增大干扰信号的功率，从而抑制了系统和速率的增长。图7.13也证明了推论7.2给出的结果的正确性。

图7.14给出了不同用户数下，莱斯因子对系统可实现和速率的具体影响。仿真中设置了基站的传输天线数M=100，总发射功率PT=15dBm，针对第k个用户传输信号的发射功率pk=PT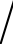 pagenumber_ebook=177,pagenumber_book=170 K，反射表面元素总个数N=300，第l块反射表面的元素个数为Nl=NK。与推论7.3给出的结论相同，由于莱斯因子可以表示为信道中视距分量与散射分量的功率之比，当莱斯因子趋近于无穷大时，信道主要受视距分量的影响。此时，系统和速率都会达到一个定值。

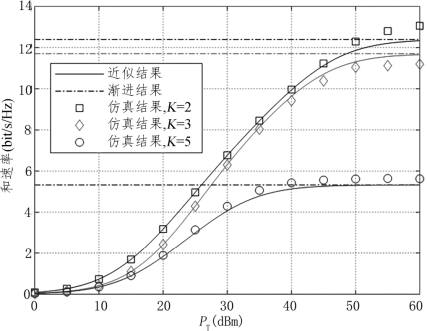
pagenumber_ebook=178,pagenumber_book=171

图7.13　不同用户数下和速率随基站总传输功率PT的变化曲线

pagenumber_ebook=178,pagenumber_book=171

图7.14　不同用户数下和速率随莱斯因子ξ的变化曲线

在前面的分析中，通过建立实际功耗模型得到系统能量效率的表达式。从式（7.61）中不难发现，基站传输功率的提升同样会增大系统能耗，同样IRS元素个数和用户数均会对能耗产生影响。图7.15比较了不同IRS元素个数N和用户数K下能量效率随传输功率PT的变化情况。仿真中设置基站天线数M=500，莱斯因子ξ=15dB。从图中可以看出，随着传输功率的不断增加，能量效率呈现先增大后减小的趋势，并在28dBm附近达到峰值。因此，从能量效率的角度出发，过高的基站传输功率不仅不会带来收益，反而会使得能量效率大幅降低。图7.15还反映出IRS元素个数的增多同样会造成损耗。

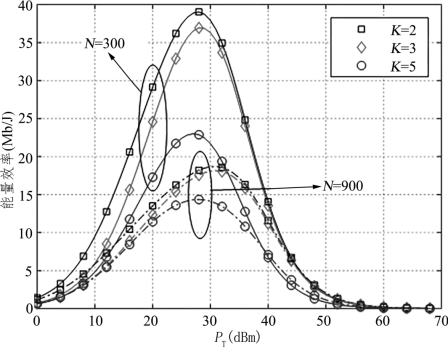
pagenumber_ebook=179,pagenumber_book=172

图7.15　不同用户数下能量效率随传输功率PT的变化曲线

图7.16在图7.13和图7.15的基础上，分析了可实现和速率与能量效率之间的权衡曲线。从横向看，可实现和速率随传输功率的增大而增大并逐渐趋于定值；从纵向看，能量效率则是先增大后减少并最终降为零。这表明，过高的传输速率不但不会带来可实现和速率的无限增大，甚至还会大幅削弱系统的能量效率。由此可见，在实际的信号传输过程中，应当选取合适的发射功率以兼顾系统可实现和速率与能量效率。以IRS元素个数N=300、用户数K=5为例，当基站传输功率约为28dBm时可以同时获得可观的可实现和速率以及能量效率。

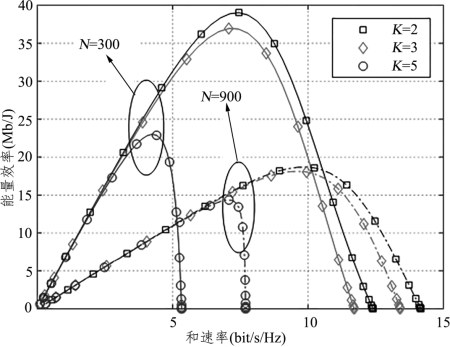
pagenumber_ebook=180,pagenumber_book=173

图7.16　不同用户数下和速率与能量效率之间的权衡曲线

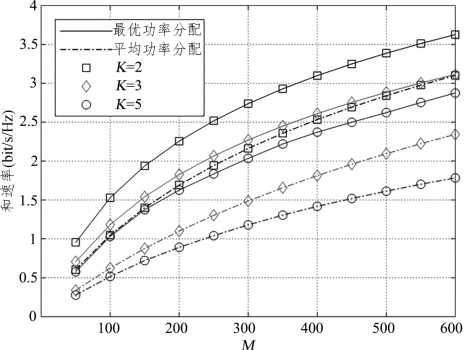
pagenumber_ebook=180,pagenumber_book=173

图7.17　不同用户数下功率分配方案对和速率的影响曲线

图7.17给出了最优功率分配方案对可实现和速率的影响。作为对比，图中虚线所示的曲线是系统在平均功率分配方案下的性能表现。从图中可以看出，最优功率分配方案下的系统性能优于平均功率分配，这在用户数较多时尤为明显。以用户数K=5为例，当基站天线数M=600时，相比于平均功率分配，所提出的最优功率分配方案可以得到61%左右的性能提升。另外，若系统目标速率为1.75bit/s/Hz，平均功率分配方案下所需的传输天线数约为600，而最优功率分配方案下仅需约250根天线。因此，在大规模MIMO系统中，合理分配发射功率既能有效提高系统性能，又能节省资源避免不必要的消耗。

IRS多用户系统仿真结果及分析

相关推荐