对IRS_SM系统进行ML检测，误比特率Pb的联合上界为其中，MΓ由接收天线指标m错误或正确检测概率所决定，可通过考虑其相关高斯分量的一般二次型来推导。根据式和中心极限定理，随着N的增加而服从复高斯分布，但是我们需要考虑它们分量之间的相关性。假设g=，经过计算，可得g的期望与方差将上式代入二次型高斯随机变量的MGF计算式中：即可得出Γ1+Γ2的矩母函数MGF，进而得到误码率。......
2023-08-23
高速铁路车地间多跳协作通信技术：系统误码率性能分析
【摘要】：对IRS_SM系统进行ML检测，误比特率Pb的联合上界为其中，MΓ由接收天线指标m错误或正确检测概率所决定，可通过考虑其相关高斯分量的一般二次型来推导。根据式和中心极限定理，随着N的增加而服从复高斯分布，但是我们需要考虑它们分量之间的相关性。假设g=，经过计算，可得g的期望与方差将上式代入二次型高斯随机变量的MGF计算式中：即可得出Γ1+Γ2的矩母函数MGF，进而得到误码率。
精确的理论误码率难以获得，考虑先推导出对天线指标m和传输数据符号x联合检测的成对差错概率PEP，以此得到误码率的上界。
对IRS_SM系统进行ML检测，误比特率Pb的联合上界为
其中，MΓ（s）由接收天线指标m错误或正确检测概率所决定，可通过考虑其相关高斯分量的一般二次型来推导。
（1）当m=
，即正确检测到接收天线指标的情况下，考虑到Gq=
，Γ可以改写为
将其代入式（7.30），可得Bob误比特率。
（2）当m≠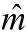
，Γ可以改写为Γ=Γ1+Γ2+Γ3，Γ1，Γ2，Γ3分别表示Γ的三种情况：q=m，q=
，q≠m且q≠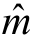
。对于不同的q，分布Gq和
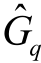以及它们之间的相关性，需要根据高斯随机变量的二次型来推导MΓ（s）。
根据式（7.33）和中心极限定理，
随着N的增加而服从复高斯分布，但是我们需要考虑它们分量之间的相关性。假设g=
，经过计算，可得g的期望与方差
将上式代入二次型高斯随机变量的MGF计算式中：
即可得出Γ1+Γ2的矩母函数MGF，进而得到误码率。对于Eve，可类比于Bob的推导。
此外，在瑞利分布的基础上，可以将其扩展为莱斯分布，根据公式（7.30），将原本信道改为莱斯分布。使用中心极限定理，
为N个独立同分布随机变量的总和，遵循复高斯分布，其均值与方差可以表示如下：
当
服从非中心卡方分布且具有一个自由度，其MGF可以表示为[180]
有关高速铁路车地间多跳协作通信技术的文章
- 详细阅读
-
高速铁路车地间多跳协作通信系统性能分析详细阅读
衡量协作通信系统性能的指标有很多，如中断概率、误码率、频谱效率、能量效率等。由于有无中继的分析方法类似，因此这里以图2.5所示的大规模MIMO下行链路为例，对几个常用的性能指标进行详细分析。图2.5所示系统中的基站天线数为M，用户数为K，基站与用户之间的信道响应为G∈CK×M。于是，用户接收到的信号为图2.5大规模MIMO系统模型其中，PS为基站的发射功率；nU∈CK×1为用户处均值为零、方差为N0的加性高斯白噪声。......
2023-08-23
-
高速铁路车地间通信多跳协作技术详细阅读
表4.1基于最大化安全容量的联合天线选择和功率分配算法2.基于拉氏乘子法的功率分配方案通过JOSCA算法能够选取出使得系统安全容量达到最优的发射天线和发射功率，根据安全容量的闭式表达式，可以发现，不管发射人工噪声的RAU的功率如何进行分配，都不会影响最终的发射天线的选择和发射有效信号功率分配因子的求解，所以可以对发射人工噪声的功率进一步分配以明确冗余的RAU分别使用多大的功率。......
2023-08-23
-
高速铁路车地间多跳协作通信技术详细阅读
由于精确的误比特率难以获得，本文通过推导成对差错概率来获得平均误比特率的上界。在瑞利道下，类似文献[158]相关的推导，得到Bob的接收误比特率为其中，为发射端与Bob的信道系数方差。对于Eve，可以将人工噪声表达为信道噪声的一部分，从而Eve接收误比特率为考虑到实际情况下，Eve端无法得到反馈的CSI。因此，对于Eve来说，最终的误比特率可以近似表示为[163]......
2023-08-23
- 详细阅读
-
高速铁路车地间多跳协作通信技术的仿真结果和分详细阅读
本节将通过仿真来验证所提出抗干扰方案的优势和性能。如表7.1所示，部分DNN训练集的输入输出参数经过模型训练后能够得到预测结果，关于DNN模型的相关参数隐藏层的个数为6层，经过调试，将各层神经元的个数设置为500，1000，1500，2000，800和300。图7.8存在干扰机时，不同速度下的误码率比较图7.9分析了不同IRS到用户的距离下，误码率受莱斯因子和IRS天线个数以及SNR的影响比较。......
2023-08-23
-
高速铁路车地间多跳协作通信技术数值分析结果详细阅读
为了验证提出的离散中继混合预编码算法的有效性，本节通过使用MATLAB对毫米波中继系统的频谱效率进行仿真分析。图5.12为信息流数与RF链个数相同时，中继接收端与中继发送端单独进行量化时频谱效率随SNR变化曲线。图5.14不同量化精度下频谱效率随天线数变化曲线图5.15为不同量化精度下中继混合预编码的能量效率随信噪比的变化曲线。随着频谱效率不断增加，能量效率将达到峰值；但当再小幅度增加频谱效率时，能量效率将大幅度下降。......
2023-08-23
-
高速铁路车地间多跳协作通信技术的仿真与分析结详细阅读
图6.2所提算法与其他算法的MSE性能比较由于完美信道为非完美信道下更能展现算法性能的一个特例情况，因此首先对于完美信道下的中继混合预编码设计进行仿真分析。图6.6中继接收与发送采用不同量化位时SE随量化位数变化曲线图6.7显示了利用不同分辨率PSs时的EE性能。这是因为与3位分辨率的情况相比，具有1位分辨率PSs的可实现SE的退化是显著的。......
2023-08-23
相关推荐