自适应天线选择方案基于深度神经网络

2023-08-23 理论教育版权反馈

【摘要】：然后，提出一种基于空时相关系数的特征选取方式替代传统的信道特征，并对天线选择方案做分解，以使得DNN模型能够有更好的拟合效果。

这一小节将基于深度神经网络算法对IRS-SM的联合天线选择问题进行优化。首先，通过分析IRS-SM的联合天线选择问题，确定输入DNN模型的参数和所要得到的输出参数。然后，提出一种基于空时相关系数的特征选取方式替代传统的信道特征，并对天线选择方案做分解，以使得DNN模型能够有更好的拟合效果。最后，对产生的数据集进行优化预处理，并设置对应的DNN全连接训练模型。

1.天线选择联合优化问题分析

为了进一步提升高铁IRS-SM的BER性能，欧式距离往往是优化的重要一环。对于一个给定的信道矩阵H，对应的欧式距离可以表示为

其中，括号内的值表示信号与估计信号的差值形成的信号对矢量。联合的优化问题便是从天线集合中选取使得欧式距离最大的天线集合，优化问题可以表示为

pagenumber_ebook=150,pagenumber_book=143

在这些设计中，关于IRS天线单元的激活选择和接收空间调制索引天线的选择是相互独立的。由于IRS的天线单元数过多，而且要对其具体的天线是否激活做出判断，则有很多的组合情况（此处计算组合情况），同时，还需要将接收空间调制索引天线联合选出来，因为这关系到视距路径与非视距路径的联合最大化问题。但是要需求全局最优解需要通过遍历的搜索，找到所有可能的等效信道矩阵和所有不同的误差向量，这必然会导致高复杂性和反馈负载。然而，负载减少在实际通信系统中的适用性是有限的。代替直接解决的问题（7.11）通过使用优化驱动决定，将它们转换为深度神经网络分类问题，在最优解可以通过低数据驱动的预测，而不是繁琐的计算。

估计IRS-SM中天线集合的对应映射，将问题转化为考虑IRS天线单元选择和接收空间调制索引天线选择这两者的联合优化问题。设IRS-RSM联合天线选择集合为，用rm表示第m个预测向量的最优表示为

其中，I（·）表示映射函数。所以，被选择的预测向量对应的元素将会是1，其他元素则为0，这就意味着只有一个映射被选择。监督学习分类器和DNN的目标都是基于可获得的训练数据来预测这个向量。

2.基于空时相关性的特征选取与方案优化

设计监督学习分类器和DNN算法应该包含两个角度，分别为训练预处理和学习系统搭建。训练预处理的过程包含有训练数据生成、特征矢量提取、关键性能指标设计和标签化这四个步骤。

（1）训练数据生成：与文献[128]和文献[129]类似，信道状态信息是影响高铁无线通信系统最重要的数据。将系统的两段无线信道合为一段进行处理，第一段为由基站发向IRS的信道gLoS，第二段为由IRS发向高速列车的信道，根据公式（7.2）进行训练数据的生成，其中，需要对不同速度v，不同场景K，不同发射信号功率（即SNR）下进行假设，其他关于角度的数据根据分布随机生成。

（2）特征矢量提取：在生成了相关的数据之后，我们需要提取相关的特征，并将这些特征作为输入集送入DNN构建模型。由前文的高铁无线信道分析，可以知道高铁信道状态特征主要由以下几个特征决定，尤其是空时相关性，可以用期望表示

pagenumber_ebook=152,pagenumber_book=145

其中，G为总的无线信道，如果根据第二章的内容，信道特征中的大尺度衰落主要与当前的位置有关系，而小尺度衰落需要考虑时间相关性，可以转化为与速度和频率相关的时间相关系数，这些都会影响到最终的天线选取结果和相位优化方式。

（3）关键性能指标设计：关键性能指标是用来区分训练样本的性能矩阵。为了进一步提升高铁无线通信系统的保密速率和BER，将系统的接收SNR作为主要KPI。

（4）标签化：在DNN模型中，需要对训练的结果标签化，这样才能有清晰的分类结果，以便模型进行更好地学习和类别区分。

另外，由于分类器的复杂度和数据集问题，需要对其进行优化。首先，由于需要将IRS的天线与空间调制接收天线进行联合选取，所以组合数十分庞大，因此，先对所有的组合数进行预处理。由于IRS天线单元与接收空间调制索引天线之间是独立的，所以可以通过使用交替优化的方法，固定接收空间调制索引天线，对IRS天线单元进行优化选取和相位调整，选取之后再对接收空间调制索引天线进行选取。

接下来，输入输出数据集的设置将会影响DNN模型做出判别，因为DNN所做的决策都是在隐藏层，所以可以被认为是黑箱模型，而只有通过输出的结果直接分析输入数据的好坏，那么输入数据就不能带有明显的倾向，需要对输入数据集进行均衡操作。一方面，数据均衡需要输入的数据集之间没有强相关性数据均衡需要对每一类的数据尽量做到平衡，尤其是得到同一个标签的样本最好接近，不然会造成训练处的结果靠近样本多的标签，所以需要对数据进行均衡化，使得标签与标签之间保持相对独立。另一方面，在输出层将天线组合作为标签的情况下，减小标签的分类可以增大标签类别之间的辨识度。在本文中，将IRS天线单元原先的组合数标签集转化为激活的天线数标签集，得到激活的天线数输出之后再进行遍历，这样就可以减小模型训练的时间复杂度以及提升模型分类的准确率。

3.深度神经网络训练

首先，搭建DNN算法的总体框架，如图7.3所示，除了输入层和输出层以外，设所提出的DNN采用了Q个隐藏层，每个隐藏层都设有相同的神经元N，采取线性整流函数（RectifiedLinearUnit，ReLU）作为神经元的激活函数[126]。将从训练集G提取的特征向量fs和分类标签Bs成对作为输入第一层可以获得对应的输出为

其中，W1∈RN×1为第一层的训练权重，b1∈RN×1为第一层的训练偏置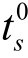， pagenumber_ebook=153,pagenumber_book=146 =fs为输入层。

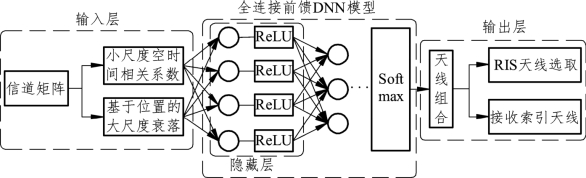
pagenumber_ebook=153,pagenumber_book=146

图7.3　前馈DNN全连接训练模型

那么，对于第q（1＜q＜Q）层来说，我们可以利用q-1层的输出向量来改善其输入的特征矢量，并产生输出如下：

其中，Wq∈RN×N为第q层的训练权重，bq∈RN×1为第q层的训练偏置。

最后，对于最后一层，在[0，1]区间内采用柔性最大值传输函数来表征输出矢量的元素，其结果可以表示为

通过迭代公式（7.15）到公式（7.17）的过程，基于最小交叉熵损失和函数不断训练各层的权重与偏置值，函数表示如下：

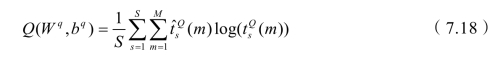
pagenumber_ebook=153,pagenumber_book=146

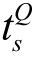其中，为根据分类标签所期望得到的值，那么对于一个新的测试集Gnew来说，就是将其特征向量fnew提取出来，重复上述步骤，并求解能够获得最大 pagenumber_ebook=154,pagenumber_book=147 的m值。

当使用第一个Q-1层增强DNN模型的拟合时，可以看作是对原始特征的细化特征提取。相比之下，最后一层被用来生成类标签。在本文中，我们采用ReLU函数作为神经元的激活函数以保证稀疏性和减少梯度消失的可能性，这有利于更快地学习天线组合分类问题。此外，如公式（7.18）所示，本章利用对数损失函数来衡量DNN分类模型的性能，因为当目标预测向量为公式（7.13）中所示的单热点向量时，便可以提高收敛速度。为了有效确定DNN多分类器中的参数{Wl，bl}，l=1，…，Q，通过简单的共轭梯度和随机梯度下降的方法将对应参数进行高效的迭代。

自适应天线选择方案基于深度神经网络

相关推荐