在本节中，通过仿真的方式验证本章前面几节所提出的理论，并详细分析速度、位置、莱斯因子K和功率分配因子α对安全容量和BER性能的影响。图4.3DSSM与现存其他方法信道容量的比较在图4.4中，详细讨论了列车位置对图4.4的遍历性SC和图4.4的合作平均SC的影响。图4.6本文所提协作DSSM与集中式传统SM的信道容量比较图4.7显示了不同莱斯因子K和相关阴影衰落方差情况下，高铁的移动速度对DSSM系统误码率性能的影响。......
2025-09-30
仿真结果与分析：高速铁路车地间多跳通信技术
【摘要】：图6.12中继位置对保密中断概率的影响曲线图6.13是信道估计误差分别为0.1、0.01、0时，系统SOP随着信噪比变化的曲线。仿真结果表明可以通过适当提高传输信噪比来抑制窃听者对系统安全性能的影响。图6.14中继数目对保密中断概率的影响曲线图6.15窃听链路信噪比对监听概率的影响曲线图6.16是剩余自干扰分别为-5dB、0dB、5dB时，监听概率随着信噪比变化的曲线。
根据以上推导结果，利用MATLAB仿真得到保密中断概率和监听概率与信噪比的关系图，并通过与蒙特卡洛仿真进行对比，验证结果的正确性。仿真中取门限速率值r=0.5bit/s/Hz，设剩余自干扰
窃听链路的平均信噪比
。根据中继所处位置不同，取
，q＞1、q＜1分别表示中继处于靠近节点A、B的位置，当q=1时表示中继恰好位于节点A与B的中间位置。
图6.12是系统SOP随中继位置变化的曲线。仿真中设置中继数目N=5、信噪比
=10dB、剩余自干扰
=0dB、窃听信噪比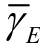
=-10dB、信道估计误差
=0.1。从图中可以看出，当
与
的比值q为1，即中继位于节点A、B中间位置时，此时系统SOP最小。中继位置越靠近A或B一侧，系统安全性能也就越差。同时，在该双向中继网络中，全双工系统的性能要优于半双工，并随着q→1，全双工系统的优势越来越大。
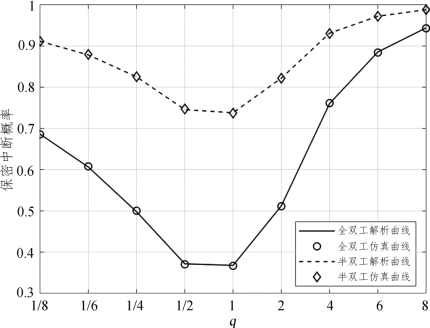
图6.12 中继位置对保密中断概率的影响曲线
图6.13是信道估计误差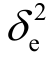
分别为0.1、0.01、0时，系统SOP随着信噪比
变化的曲线。仿真中设置中继数目N=5、窃听信噪比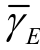
=-10dB、剩余自干扰
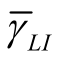=-5dB，并取
，即中继位于靠近节点B的位置。从图中可以看出，随着信道估计误差的增大，SOP逐渐增大，相应地系统性能逐渐变差。在信噪比
较低时，这种变化尤为明显。当
增大到一定值时，SOP趋近于稳定，信道估计误差不再是影响系统性能的主要因素。在同一条件下全双工系统的安全性能明显优于半双工系统。
图6.13 信道估计误差对保密中断概率的影响曲线
图6.14是中继数目N取1、3、5时，系统SOP随着信噪比
变化的曲线。仿真中设置q=1
2、窃听信噪比
=-10dB、剩余自干扰
=-5dB、信道估计误差
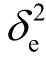=0.1。当N=1时即为单中继系统。从图中可以看出，系统SOP随着信噪比的增加而减少，中继数目越多，系统SOP下降越明显。当信噪比增加到一定值时，系统SOP逐渐趋于稳定。在高信噪比处，N=5时的保密中断概率是N=3时的50%左右，是单中继系统的27%左右。由此可见，在传输信噪比无法满足要求的情况下，适当增加中继数目可以有效地提高系统的安全性能。(https://www.chuimin.cn)
图6.15是窃听信噪比
在0dB、-5dB、-10dB三种情况下，监听概率随着信噪比
变化的曲线。仿真中设置q=1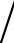
2、中继数目N=5、剩余自干扰
=0dB、信道估计误差
=0.1。从图中可以看出，随着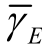
的下降，监听概率大幅下降，系统的安全性能明显上升。由于半双工系统中没有剩余自干扰的影响，在低到中信噪比处，同一条件下半双工系统的监听概率要低于全双工系统的监听概率。同时这种影响随着信噪比的提升逐渐消失。仿真结果表明可以通过适当提高传输信噪比来抑制窃听者对系统安全性能的影响。
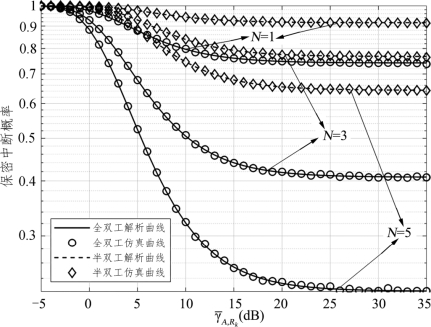
图6.14 中继数目对保密中断概率的影响曲线
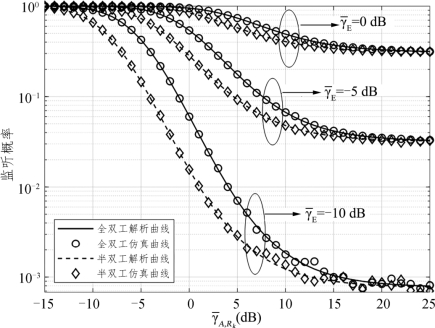
图6.15 窃听链路信噪比对监听概率的影响曲线
图6.16是剩余自干扰
分别为-5dB、0dB、5dB时，监听概率随着信噪比
变化的曲线。仿真中设置q=1
2、中继数目N=5、窃听信噪比
=-10dB、信道估计误差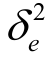
=0.1。从图中可以看出，系统的监听概率随着剩余自干扰
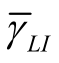的降低而降低，而半双工系统中剩余自干扰为零，因此半双工系统的监听概率总是低于全双工系统的监听概率。随着信噪比
的逐渐增加，剩余自干扰带来的影响逐渐减弱。当
增加到一定值时，半双工与全双工系统的监听概率几乎保持一致，此时剩余自干扰不再是影响系统安全性能的主要因素。
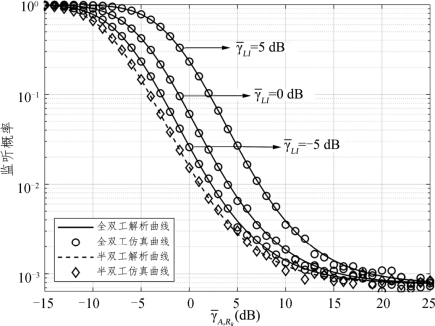
图6.16 剩余自干扰对监听概率的影响曲线
相关文章
- 详细阅读
-
多跳通信技术在高速铁路车地间的应用详细阅读
图5.2显示了在不同DAC量化位数下可实现和速率随基站天线数NB变化的近似分析和蒙特卡罗仿真曲线。图中的实线和虚线分别表示莱斯和瑞利衰落信道两种情况，对应于定理5.1中的结论。从图中可以看出，近似分析和蒙特卡洛仿真曲线非常接近，证实了结果的准确性。而式和式显示出系统功耗随DAC量化位数的增大呈指数级别增长。......
2025-09-30
-
高速铁路车地间多跳协作通信技术详细阅读
由于精确的误比特率难以获得，本文通过推导成对差错概率来获得平均误比特率的上界。在瑞利道下，类似文献[158]相关的推导，得到Bob的接收误比特率为其中，为发射端与Bob的信道系数方差。对于Eve，可以将人工噪声表达为信道噪声的一部分，从而Eve接收误比特率为考虑到实际情况下，Eve端无法得到反馈的CSI。因此，对于Eve来说，最终的误比特率可以近似表示为[163]......
2025-09-30
- 详细阅读
-
高速铁路车地间多跳协作通信技术中的应用详细阅读
接下来，我们将关注问题的多预编码矩阵联合优化问题，其中等价目标函数通过以下过程重新制定，以适应基本ADMM解决方案框架。近似解可计算为为了确保优化结果满足功率约束，需要通过求解子优化问题来额外计算松弛的数字预编码矩阵，其拉格朗日函数由下式给出：其中，ε≥0为拉格朗日乘子。......
2025-09-30
-
高铁车地间多跳通信技术详细阅读
另外，当源节点与目的节点间由于障碍物的影响而无法正常通信时，通过引入协作中继可以消除通信链路的盲点，降低中断概率，提高系统性能并获得更高的增益。随后Covel等人对中继信道进行了深入的研究，并给出了系统容量的上下限，奠定了协作通信技术的理论基础[18]。图1.3高速铁路场景下的协作通信系统多中继协作通信还能利用物理层特性提高信息传输的安全性。现有的物理层安全技术主要是通过MIMO和中继技术来实现的[27]。......
2025-09-30
- 详细阅读
-
高速铁路车地间多跳协作通信技术的性能分析详细阅读
系统的SC为合法信道容量与窃听信道的信道容量的差值其中，P表示传输功率；表示合法信道的噪声方差；表示窃听信道的噪声方差。反之，则系统的SC为0，不具备保密能力，无法实现信息的安全传输。当信道为复加性高斯白噪声信道时，系统的SC为2.误比特率性能分析SM信号经过MLD算法检测后，由于精确的误比特率难以获得，本文通过推导成对差错概率来获得平均误比特率的上界。......
2025-09-30
相关推荐