高速铁路车地间多跳协作通信技术：离散车辆中继混合预编码设计

2023-08-23 理论教育版权反馈

【摘要】：通过使用量化移相器且在系统总功率的约束下，中继混合预编码优化问题可以转化为为了求得公式中的最大化频谱效率，需要设计每个节点的混合预编码器。故本节将主要针对中继节点的量化进行求解，不对源节点与目的节点进行赘述。与点对点系统不同的是，中继混合预编码稀疏近似问题具有两个天线阵列响应矩阵，并且需要对其进行联合求解。根据最小二乘原理对中继数字预编码矩阵求解。

针对中继混合预编码问题，通过联合公式（5.57）与公式（5.58），则毫米波中继大规模MIMO系统的频谱效率可以表示为

其中，为有效接收信号的协方差矩阵；Rn为噪声和干扰的协方差矩阵。具体表示为

为了求得最大化的系统频谱效率，需要对所有的模拟与数字预编码器进行联合设计。模拟预编码器通过使用移相器对相位进行调整，将移相器的值量化为以δ=2π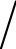 pagenumber_ebook=106,pagenumber_book=99 2B为量化单位的具有2B个有限数量元素的量化集合Φ。该集合表示为

其中，B为最大量化精度。根据量化移相器的取值，所有模拟预编码器中m行n列元素的恒模约束转变为

其中，Γ为所有模拟预编码器的集合。通过使用量化移相器且在系统总功率的约束下，中继混合预编码优化问题可以转化为

为了求得公式（5.66）中的最大化频谱效率，需要设计每个节点的混合预编码器。其中源节点与目的节点的优化问题为传统点对点优化问题，其约束条件仅与其自身节点预编码矩阵有关，而与其他节点的预编码矩阵无关。因此，可以通过迭代算法来对源节点与目的节点的优化问题进行求解，如采用基于几何平均分解算法求得源节点与目的节点的混合预编码矩阵F和W。故本节将主要针对中继节点的量化进行求解，不对源节点与目的节点进行赘述。

将联合优化问题（5.66）进行解耦，分离各个节点的恒模约束与功率约束，其中分离重构后的中继节点优化问题表示如下：

其中，目标函数设置为最大化该系统频谱效率，优化约束为中继节点的功率约束与中继节点模拟预编码器的恒模约束。

针对所分解出的中继端混合预编码优化问题，由于该优化问题需要对三个预编码矩阵进行联合优化，并且该优化问题同时具有恒模约束与功率约束的非凸约束条件，因此对混合预编码问题分离非凸约束与功率约束，并基于稀疏近似方法进行求解。暂不考虑模拟预编码器的量化影响，并将优化问题转换为范数最小化问题，即

通过优化公式（5.68）可以求得最佳数字预编码矩阵与最佳模拟预编码矩阵。然而其所求得的模拟预编码矩阵仍然是基于无限量化精度移相器，因此需要对模拟预编码器进行量化。定义量化函数

其中，为τm，n的量化值；量化器Q将输入的τm，n量化为距离量化集合Φ最近的一个点后并输出量化值。将模拟预编码器的每一个元素分别通过量化器，以此得到量化后的模拟预编码矩阵。

与点对点系统不同的是，中继混合预编码稀疏近似问题具有两个天线阵列响应矩阵，并且需要对其进行联合求解。本文所提出的求解算法主要步骤如下：

（1）将接收天线响应矩阵AR中与残差矩阵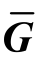 pagenumber_ebook=109,pagenumber_book=102 最相关的行r赋值于接收模拟预编码矩阵GR。

（2）根据公式（5.70）对获取的接收模拟预编码矩阵GR中每个元素进行量化处理，并重构GR。

（3）将发送天线响应矩阵AT与接收模拟预编码矩阵GR和残差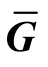 pagenumber_ebook=109,pagenumber_book=102 共同相关的列c，赋值于发送模拟预编码矩阵GT。

（4）通过与接收端相同的量化方式对GT进行量化。

（5）根据最小二乘原理对中继数字预编码矩阵求解。

（6）通过计算无约束预编码器与混合预编码器之间归一化距离来对残差进行更新。

（7）对功率约束进行设计。

本算法通过步骤2、步骤4进行迭代求解混合预编码矩阵，其中步骤2的时间复杂度为，步骤4的时间复杂度为。通过利用步骤 1 与步骤 3进行外部迭代，其功能为将模拟预编码矩阵中每一列进行单独投影计算，其复杂度为。综合计算步骤1、步骤2、步骤3、步骤4的时间复杂度，则系统总的时间复杂度为，其中，为中继接收端与发送端之间最大量化精度；为中继接收端与中继发送端之间最大天线数。

高速铁路车地间多跳协作通信技术：离散车辆中继混合预编码设计

相关推荐