多跳通信技术在高速铁路车地间的应用

2023-08-23 理论教育版权反馈

【摘要】：图5.2显示了在不同DAC量化位数下可实现和速率随基站天线数NB变化的近似分析和蒙特卡罗仿真曲线。图中的实线和虚线分别表示莱斯和瑞利衰落信道两种情况，对应于定理5.1中的结论。从图中可以看出，近似分析和蒙特卡洛仿真曲线非常接近，证实了结果的准确性。而式和式显示出系统功耗随DAC量化位数的增大呈指数级别增长。

在本节中，验证了具有低精度DAC的多用户大规模MIMO下行链路可实现和速率以及能量效率的近似分析和蒙特卡罗模拟结果。在仿真中，设置用户数K=10，噪声功率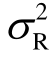 pagenumber_ebook=98,pagenumber_book=91 =2.2dB、=1.3dB。通过文献[175]中的类似分析，两跳信道中的大规模衰落分别建模为，其中路径损耗v=2.4，参考距离dref=100m，dBR表示基站与中继之间的距离，dRU，k表示中继与第k个用户之间的距离。建立以米为单位的笛卡儿坐标系，以基站所在的位置为坐标原点（0，0），中继坐标为（500，0），用户坐标为{（980，199），（993，145），（997，90），（999，51），（1002，22），（1000，0），（998，-34），（994，-83），（989，-136），（979，-187）}。同时，在莱斯衰落信道中，假设ξh，k=ξ，且到达角（Angle-of-Arrival，AoA）θh，m在区间内均匀分布。

图5.2显示了在不同DAC量化位数下可实现和速率随基站天线数NB变化的近似分析和蒙特卡罗仿真曲线。仿真中，假定基站和中继的DAC量化位数相同，即b1=b2=b。设置PB=28dB，PR=25dB，λ=1，莱斯因子ξ=10dB。图中的实线和虚线分别表示莱斯和瑞利衰落信道两种情况，对应于定理5.1中的结论。从图中可以看出，近似分析和蒙特卡洛仿真曲线非常接近，证实了结果的准确性。随着基站天线数量的增加，可实现和速率也相应增加。DAC量化位数越大，和速率就越大，但是增长率会放缓。同时，图5.2中显示了DAC量化精度的降低是以增加天线数量为代价的。这也从另一个方面表明，在低精度DAC中，可以通过增加基站天线数量来改善系统性能。

尽管基站和中继处都配备了低精度DAC，但由于它们在系统中的作用不同，增加相同级别的DAC量化位数将带来不同的性能。推论5.2对大规模天线阵列下的这种性能差异进行了定性分析，图5.3给出了五组不同的DAC量化位数对应的可实现和速率变化曲线。在仿真中，设置PB=28dB，PR=25dB，λ=5，ξ=10dB。以NB=1500为例，与（b1，b2）=（1，1）相比，（b1，b2）=（1，2）带来的和速率的提升约为（b1，b2）=（2，1）时的6.6倍。由（b1，b2）=（1，∞）带来的和速率的提升可以达到（b1，b2）=（∞，1）的7.5倍。因此，从可实现和速率的角度来看，与基站相比，增加中继处的DAC量化位数更有价值。

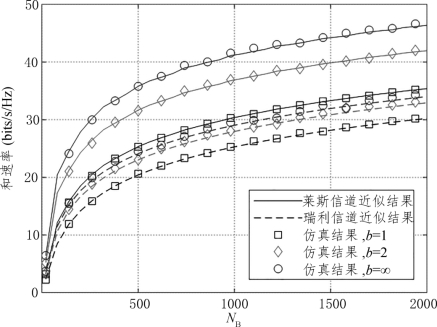
pagenumber_ebook=99,pagenumber_book=92

图5.2　理想CSI下不同DAC量化位数b的和速率与基站天线数NB的变化曲线

pagenumber_ebook=99,pagenumber_book=92

图5.3　理想CSI下不同DAC量化位数b1和b2的和速率随基站天线数NB的变化曲线

图5.4展示了在理想和非理想CSI信道中，不同量化位数b下，可实现和速率随发射功率PB变化的近似分析和蒙特卡洛仿真曲线。在仿真中，假定PB=PR=20pp，τ=K，b1=b2=b，NB=100，λ=1，莱斯因子ξ=0dB。从图中可以看出，当PB较小时，随着发射功率的增加，可实现和速率迅速增加。当发射功率PB继续增加时，与信道中的加性高斯白噪声相比，系统中的量化噪声起主要的限制作用。此时，可实现和速率的增速开始减慢并最终达到饱和点，这与推论5.3中的结论一致。另外，从图5.4可以看出，提高导频发射功率和DAC量化位数可以提高信道估计的精度。

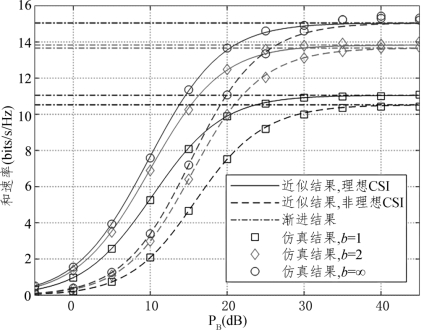
pagenumber_ebook=100,pagenumber_book=93

图5.4　理想和非理想CSI下不同DAC量化位数b的和速率随基站发射功率PB的变化曲线

图5.5中展示了在理想和非理想CSI信道中，不同DAC量化位数b下莱斯因子对可实现和速率的影响。仿真设置发射功率PB=28dB，PR=25dB，PR=20pp，τ=K，b1=b2=b，NB=500，λ=5。图中的渐近下限和上限分别表示莱斯因子为零和无穷大的情况。数值结果表明，在这两种极端情况下，莱斯因子都不是影响系统可实现和速率的主要因素。特别是，当莱斯因子不断增加时，理想CSI和非理想CSI下可实现和速率将达到相同的定值。此外，图中也显示了莱斯因子对可实现和速率的影响范围有限。

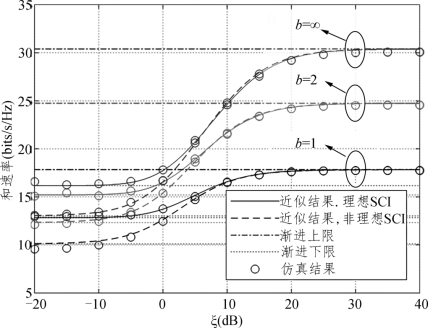
pagenumber_ebook=101,pagenumber_book=94

图5.5　理想和非理想CSI下不同DAC量化位数b1的和速率随莱斯因子ξ的变化曲线

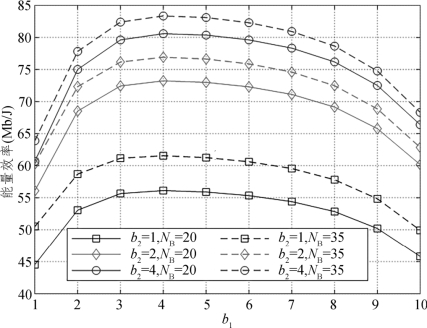
pagenumber_ebook=101,pagenumber_book=94

图5.6　理想CSI下不同基站天线数NB和b2的能量效率随DAC量化位数b1的变化曲线

在图5.6中，比较了理想CSI信道中，不同的b2和NB下系统能量效率随b1的变化曲线。仿真中设置PB=28dB，PR=25dB，λ=1和ξ=10dB。从图中可以看出，随着DAC量化位数的逐渐增加，能量效率先上升后下降，并在DAC量化位数为4时达到峰值。这是因为DAC量化位数对可实现和速率以及功耗有着不同的影响。图5.2已经展示出，随着DAC量化位数的增加，可实现和速率的增速逐渐变慢。而式（5.32）和式（5.34）显示出系统功耗随DAC量化位数的增大呈指数级别增长。具体来说，当DAC量化位数从1增加到4时，可实现和速率的增速要快于系统功耗，因此能量效率呈现上升趋势。当DAC量化位数继续增加时，可实现和速率仅略有增加，而功耗却显著增加，因此此时能量效率开始呈现下降趋势。结果表明，适当增加DAC量化位数可以改善系统能效，而高精度DAC量化不仅不能提高能量效率，反而会造成系统损耗。

为了清晰显示b1、b2和NB对可实现和速率以及能量效率的影响，图5.7在图5.6的基础上分析了二者之间的权衡曲线，其中每一条曲线都是由图5.6中横坐标b1的值对应的和速率，能量效率构成。从图中可以看出，当b1=4时，系统的能量效率与可实现和速率均达到最大值。随后，随着量化位数的增加，可实现和速率几乎保持不变，而能量效率急剧下降。因此，在本章中提出的大规模MIMO中继辅助下行链路中，较低精度的DAC量化不仅可以带来可观的能量效率，还可以确保可观的和速率。

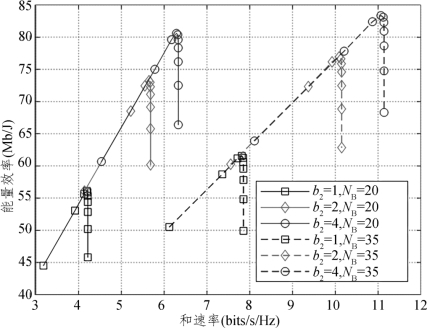
pagenumber_ebook=102,pagenumber_book=95

图5.7　理想CSI下不同基站天线数NB和b2的和速率与能量效率之间的权衡曲线

图5.8显示了在几组不同的功率缩放水平下，可实现和速率与天线数量间的关系曲线。仿真中设置EB=38dB，ER=45dB，λ=2，b1=b2=∞，ξ=0dB。根据定理5.2中的分析，取（m，n）为（1.5，1.5）、（2，1）、（1，2）、（2，2）、（2.5，2.5）五组数据进行验证。显然，近似曲线所示的结果最终都趋近于渐近曲线，这证明了定理5.2中结论的准确性。从图中还可以看出，在m＜2和n＜2时进行功率缩放，可以获得最佳性能。相反，当m＞2或n＞2时，随着NB的增加，发射功率被严重抑制，导致可实现和速率持续降低，最终衰减为零。在其他三种情况下，可实现和速率都会受到不同程度的抑制。

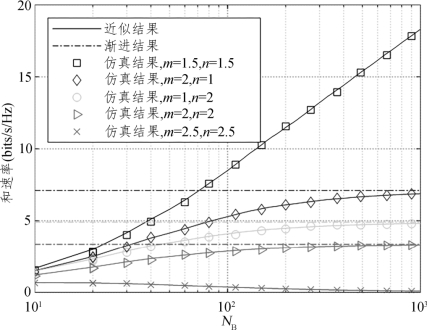
pagenumber_ebook=103,pagenumber_book=96

图5.8　理想CSI下不同功率缩放情况的和速率随基站天线数量NB的变化曲线

图5.9验证了局部最优功率分配方案的结论，其中用圆圈标记点的横坐标表示在该情况下由式（5.45）得出的最优功率分配因子。在仿真中，设置总发射功率PT=10dB，NB=250，λ=1，b1=b2=b，ξ=10dB，并设置了两组不同中继位置的结果作对比。从图中可以看出，当dBR不变时，DAC量化位数b的变化对α*几乎没有影响，但有助于改善用户获得的信干噪比。在总发射功率较低和其他参数不变的情况下，基站和中继之间的距离dBR对α*具有很大影响。当中继处于基站和用户间的中间位置，此时α*≈0.25，即当PR≈3PB时可以获得最高的信干噪比。随着基站逐渐接近用户一侧时，获得最高信干噪比所需的中继发射功率PR开始减少。此外，以b=∞为例，与dBR=500m相比，dBR=700m时用户获得的信干噪比增加了约37%。

pagenumber_ebook=104,pagenumber_book=97

图5.9　完美CSI下的SINR随功率分配因子α的变化曲线

多跳通信技术在高速铁路车地间的应用

相关推荐