首页理论教育误差传播定律-《测量员：专业技能入门与精通》编写

误差传播定律-《测量员：专业技能入门与精通》编写

2023-08-20 理论教育版权反馈

【摘要】：阐述观测值中误差与观测值函数中误差之间关系的定律称为误差传播定律。+Knxn 式中，K1、K2、Kn为常数，x1、x2、xn为独立观测值；相应的中误差为mx1、mx2、…解：根据式得例3-6 在1∶1000地形图上量得A、B两点间的距离d=234mm，中误差md=±0.1mm，求A、B间的实际水平距离D的中误差mD。例3-8 如图3-1所示，测得AB的竖直角α=30°00′00″±30″，平距AC为D=200.00m±0.05m，求A、B两点间高差h及其中误差mh。

当对一量进行了多次观测，就可以根据观测值计算出观测值的中误差，作为衡量观测结果精度的标准。但是，在测量工作中有些未知量往往不是直接测得的，而是通过量测其他一些有关的量以后，间接计算出来的。例如水准测量中，在一测站上测得后、前视读数分别为a、b，则高差：h=a-b，这里高差h是直接观测值a、b的函数。显然，当a、b存在误差时，h也受其影响而产生误差。这种关系称为误差传播。阐述观测值中误差与观测值函数中误差之间关系的定律称为误差传播定律。

下面分两种情况进行讨论。

1.线性函数的中误差

设有线性函数

z=K₁x₁+K₂x₂+…+K_nx_n （3-15）

式中，K₁、K₂、K_n为常数，x₁、x₂、x_n为独立观测值；相应的中误差为m_x1、m_x2、…、m_xn；函数z的中误差为m_z。

根据中误差的定义，得z的中误差为

（1）对于和差函数

z=±x₁±x₂±…±x_n可推得

如果m_x1=m_x2=…=m_xn=m，则

（2）对于倍数函数z=Kx，有

m_z=Km_x （3-19）

例3-4 有一矩形，丈量两条边的长度为a=40.00m±0.03m，b=20.00m±0.02m，试求矩形的周长P及其中误差m_P。

解：矩形的周长为

P=2a+2b=（2×40.00）m+（2×20.00）m=120.00m

例3-5 用30m钢尺丈量120m距离，共分4个尺段进行丈量，若每尺段丈量中误差m₃₀为±3mm，计算全长中误差m₁₂₀。

解：根据式（3-16）得

例3-6 在1∶1000地形图上量得A、B两点间的距离d=234mm，中误差m_d=±0.1mm，求A、B间的实际水平距离D的中误差m_D。

解：按式（3-19）得

m_D=1000m_d=1000×（±0.1）mm=±100mm

例3-7 已知用某台经纬仪测量水平角，每测回角度中误差为±10″。今用这台仪器测一角度，要求测角中误差不超过±5″，问至少需要观测几个测回？

解：按式（3-13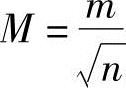），。因为m=±10″，M=±5″，所以

2.非线性函数的中误差

设有非线性函数为Z=f（x₁，x₂，…，x_n）

式中，x₁，x₂，…，x_n为直接观测值；中误差分别为m₁，m₂，…，m_n；函数Z的中误差为m_Z。

式中，是函数对各独立观测值x_i的偏导数。

例3-8 如图3-1所示，测得AB的竖直角α=30°00′00″±30″，平距AC为D=200.00m±0.05m，求A、B两点间高差h及其中误差m_h。

解：A、B两点间高差为h=Dtanα=200.00mtan30°=115.47m

图 3-1

对函数式求其偏导数得