首页理论教育测量员：算术平均值及误差

测量员：算术平均值及误差

2023-08-20 理论教育版权反馈

【摘要】：在实际工作中，是取算术平均值代替真值，将算术平均值与各次观测值之差，作为改正数代替真误差，由此推导出用改正数表示的中误差计算公式。根据误差理论可知，若观测值的中误差为m，则算术平均值中误差mx为或由式可见，算术平均值的精度高于每一观测值的精度。表3-2 各次观测值解：例3-3 对某角进行5次观测，各次观测值列于表3-3，试计算其算术平均值及其中误差。

1.算术平均值

对某量进行n次等精度观测，取其算术平均值作为最后结果，就是这个观测量的最可靠值，又称最或然值。现证明如下

Δ₁=L₁-X

Δ₂=L₂-X

  

Δn=Ln-X

等式两边相加得

Δ₁+Δ₂+…+Δn=L₁+L₂+…+L_n-nX

或 [Δ]=[L]-nX

等式两边除n得

令

代入得X=x-δ

δ为n次观测值真误差的平均值，根据偶然误差的第四特性，当n→∞时，δ→0。

即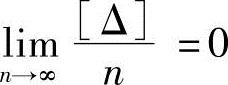

因此得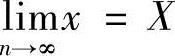

由式（3-8）可知，如果对某一量的观测次数n趋向无限多时，观测值的算术平均值就趋向该量的真值。在实际工作中，对某一量的观测次数总是有限的，根据有限次观测值求出的算术平均值就不是真值了，但可认为是观测的最可靠的结果。

2.观测值中误差

根据式（3-4）计算中误差m，需要知道观测值L_i的真误差Δ_i，但所求量的真值往往是未知的，所以真误差亦无法求得。在实际工作中，是取算术平均值代替真值，将算术平均值与各次观测值之差，作为改正数代替真误差，由此推导出用改正数表示的中误差计算公式。设L₁，L₂，…，L_n为一组等精度的观测值，x为观测值的算术平均值，V表示改正数，即

V₁=x-L₁

V₂=x-L₂

（3-9）



V_n=x-L_n

等式两端相加得

[V]=nx-[L]

由式代入上式

[V]=0 （3-10）

即对某量的一组等精度观测值，其改正数的代数和应等于零。这一性质可作为计算检核用。

下面先讨论V_i与Δ_i之间的关系，从而导出以改正数V_i表示的观测值中误差的公式。由式（3-3）得

Δ₁=L₁-X

Δ₂=L₂-X

 

Δ_n=L_n-X

将上式与式（3-9）对应项相加得

Δ₁=V₁+（x-X）

Δ₂=V₂+（x-X）

  

Δ_n=V_n+（x-X）

将上式两端平方后相加得

[ΔΔ]=[VV]+2（x-X）[V]+n（x-X）²

由式（3-10）知[V]=0

则 [ΔΔ]=[VV]+n（x-X）²

等式两端除以n得

式（3-11）等式右边第二项为

由于Δ₁，Δ₂…，Δ_n是彼此独立的偶然误差，故Δ₁Δ₂，Δ₂Δ₃，…也具有偶然误差的特性，当n→∞时，上式等号右边第二项趋于零，代入式（3-11）得

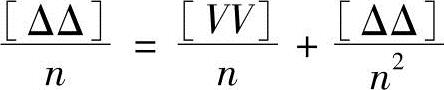
根据中误差定义公式

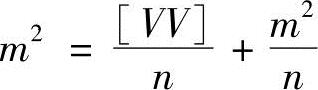
即

式（3-12）为利用观测值的改正数计算观测值中误差的公式，又称为白塞尔公式。

3.算术平均值中误差的计算公式

在衡量观测结果精度时，除了要求出观测值中误差（即每一观测值的精度）之外，还要求出观测值的算术平均值的中误差，以便评定观测值最后结果的精度。根据误差理论可知，若观测值的中误差为m，则算术平均值中误差m_x为

或

由式（3-14）可见，算术平均值的精度高于每一观测值的精度。

例3-2 对某段直线进行六次等精度的测量，各次的观测值列于表3-2，试求算术平均值及其中误差、观测值中误差和相对误差。

表3-2 各次观测值

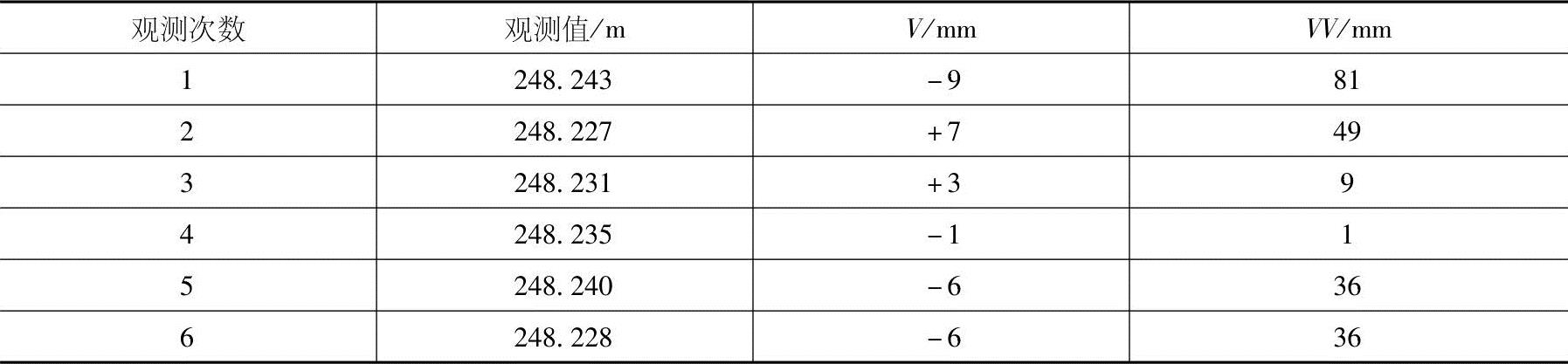
解：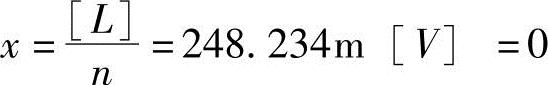

例3-3 对某角进行5次观测，各次观测值列于表3-3，试计算其算术平均值及其中误差。

表3-3 观测值

解：x=48°46′37″[V]=+2

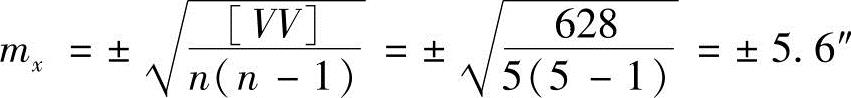
该角为48°46′37″±5.6″。