储层裂缝建模与多相流耦合理论研究的成果

2023-08-20 理论教育版权反馈

【摘要】：本小节基于基本的牛顿力学对储层平行平面裂缝流进行分析。在图中流体微元主要受到压力差和剪切力的作用，其中压力差取决于裂缝两端的水头压力差值，而剪切力则取决于裂缝中流体的流速分布。进一步分析，储层裂缝中流体在裂缝上壁面的剪切应力为：由于裂缝高度非常小，所以该剪切应力对储层固体骨架的剪切作用也非常小。

本小节基于基本的牛顿力学对储层平行平面裂缝流进行分析。在图中流体微元主要受到压力差和剪切力的作用，其中压力差取决于裂缝两端的水头压力差值，而剪切力则取决于裂缝中流体的流速分布。在图72（a）中，流体微元所受到的剪切力随着与裂缝壁面的距离缩小而增大，其中流体微元顶面所受到的剪切力大小表示为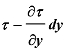 pagenumber_ebook=107,pagenumber_book=95 ，流体微元底面所受到的剪切力大小表示为τ。在图72（b）中，裂缝中流体流动方向与图72（a）中相反，但流体微元顶面所受到的剪切力大小仍可以表示为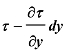，流体微元底面所受到的剪切力大小也同样可以表示为τ。

图72 储层平行平面裂缝流分析

对于图72（a）中的微流元，可以对该六面体做力平衡分析：

对该公式展开化简可得：

根据牛顿流体剪切力公式可知：

同时裂缝两端压力差为pΔ　，则压力项可以写作：

将公式（5-4）代入公式（5-3）、（5-2），则可以得到：

对于图（b）中的微流元，同样可以做力学平衡分析，只不过：

同样可以得到：

对该二次微分进行积分，可以得出速度分布公式：

其中A和B为积分常数。

对于储层裂缝，在裂缝壁面固定不动的情况下，可以设流体在裂缝壁面的流动速度为零，即：

可以定出两个积分常数为：

将积分常数代入，速度截面公式，则有：

可见，裂缝中流体流动速度最大数值，位于裂缝中心面上。

得到裂缝流速截面分布公式之后，假定裂缝宽度为B，就可以计算流量q：

其中S为裂缝截面面积。

根据渗流系数的定义，可以推断裂缝的渗流系数为：

由储层平行裂缝流假设推算出的裂缝渗透率公式可以看出，裂缝渗透率只和裂缝几何形状有关。由于裂缝渗透率和裂缝宽度为二次关系，所以裂缝渗透率对裂缝宽度的变化非常敏感。进一步分析，储层裂缝中流体在裂缝上壁面的剪切应力为：

由于裂缝高度非常小，所以该剪切应力对储层固体骨架的剪切作用也非常小。假定流体为油，裂缝为微裂缝，裂缝高度为100μ m黏度系数设定　μ=　0.1Pa .S ，裂缝两端压力差值取100m水头差Δp　=　106Pa ，裂缝长度约取为100m，按照该公式计算，则裂缝中流体流动对储层骨架架构的剪切应力为0.06Pa，所以裂缝中流体流动对储层骨架的作用是非常小的，但反过来，由储层裂缝渗透率计算公式可知，储层骨架的变化对裂缝渗透率影响却非常明显。

储层裂缝建模与多相流耦合理论研究的成果

相关推荐