储层裂缝建模及多相流耦合理论研究成果

2023-08-20 理论教育版权反馈

【摘要】：对于第二种裂缝系统反演方法，目前较为常用的方法有梯度法、牛顿迭代法、蒙特卡洛模拟法等。裂缝反演系统，就转化为求解目标函数的极值问题。因此搜索步距应当和目标函数在最新搜索点处的梯度成反比。确定了搜索方向，但还面临着裂缝反演问题中的一个重要障碍。这里，本次研究在共轭向量搜索的基础上，加入模拟退火

裂缝演化系统是一个复杂的非线性动力系统，即裂缝演化结果和介质系统的属性参数不存在线性关系。由前面的分析可知，裂缝系统是一个多因素控制的非线性问题。要解决裂缝反演问题，有两种途径。第一，将非线性裂缝演化系统进行线性化近似，然后用线性反演方法求解；第二，直接采用非线性方法对裂缝演化系统进行反演。第一种裂缝系统反演方法，虽然有较为成熟的理论，但是由上一节的分析可以看到，裂缝系统是一个高度非线性问题，尤其在裂缝尖端，存在应变场和应力场奇异化问题，如果简单采用线性化方法分析裂缝演化问题，无疑会增加问题的非唯一性，甚至导致错误的结论。对于第二种裂缝系统反演方法，目前较为常用的方法有梯度法、牛顿迭代法、蒙特卡洛模拟法等。

梯度法和牛顿迭代法是可选的求解裂缝反演非线性问题两种比较古老的反演方法。为了考察裂缝的反演分析及分布预测问题，首先建立储层裂缝扩展正向演化模型：

其中X为裂缝状态量，　Xobs为裂缝的观测量，来自勘探开发资料分析，　ϖ0为模型参量，包括地质系统的属性特征、初始裂缝条件、边界条件和断裂力学特征等裂缝演化系统参量。

设裂缝扩展系统的通解为G，将裂缝演化系统缩写为一个隐式方程：

如果将裂缝系统观测量和裂缝地质属性合并，构建一个新的参数空间为κ，则：

裂缝演化系统可以改写为：

式中，G（κ）包含了裂缝演化模型的全部方程组。

假设裂缝演化系统一共包含应变场控制方程组、储层岩石本构方程组和裂缝尖端扩展控制方程组等，这些方程组共M个方程，则有：

为了向下分析，现在设定目标函数为如下形式：

则当（）κΠ 取到最小值0时，可得到裂缝反演方程组的解。裂缝反演系统，就转化为求解目标函数的极值问题。

取目标函数在任意初始状态0κ处的发现方向为：

由于梯度方向指向目标函数增速最快的方向，则梯度方向的反方向必然是目标函数减少最快的方向。所以，从κ0处出发，沿着方向搜索，经过反复迭代，势必可以到达目标函数最小值0。模型的初始状态　0κ的位置如果离反演问题的解比较近，则经过很少的迭代，目标函数就可以到达0；如果模型的初始状态　0κ 里实际问题的解非常远，则采用较小的迭代步距势必会增加计算时间，采用较大的迭代步距，又容易错过问题的解，出现震荡，甚至不收敛。所以必须要确定一个最佳的搜索步距，从初始状态　0κ处出发，不断调整搜索步距，才能最快到达问题解。首先确定梯度方向的单位矢量为：

搜索步距假定为：，其中d即为搜索步距。下一个搜索点的坐标为：

搜索步距对于目标函数影响非常大。一般如果在新的搜索点处，目标函数 Π　（κ　i+　1）　＜Π　（κi），即新的模型参数和裂缝初始化参数，可以取到更小的目标函数，则新的搜索点更符合储层岩石基本控制规律和裂缝演化规律，说明搜索步距合适。反过来，如果在新的搜索点处，目标函数　Π　（κ　i+　1）　＞Π　（κi），则说明当前搜索点处的模型和实际地质规律符合程度不如上一个搜索点，搜索步距过大。

如何确定裂缝反演系统的搜索步距，并没有确切的最优方法。本次研究建立三种可供借鉴的方法：迭代步距法、多点控制法和固定步距法。

迭代步距法的核心思想是将最新的搜索点处的目标函数和目标函数的梯度数值作为，确定搜索步距的重要参考因素。每次迭代完，当前搜索点处的目标函数值为Π　（κi），如果Π　（κi）非常接近0，则迭代步距应当减少，如果Π　（κi）非常大，则迭代步距要取的大一些。所以迭代步距应当和Π　（κi）成正比。另一方面，如果Π　（κi）在当前搜索点处的梯度非常大，则应当减少搜索步距，因为过大的搜索步距，可能越过Π　（κi）的0值点。如果Π　（κi）在当前搜索点处的梯度非常小，则应当增加搜索步距，因为当前搜索点处目标函数变化不大，可以增大搜索步距，加快搜索过程。因此搜索步距应当和目标函数在最新搜索点处的梯度成反比。综合这两个因素，本次研究提出一种绝对值迭代步距计算方法：

其中β为一个固定常数。

第二种多点控制法。选取多个迭代步距d 1　，d　2，...dn ，计算其上的目标函数值，根据多个跌打步距上目标函数的变化趋势确定一个最有迭代步距。这种方法计算量很大，对于复杂的裂缝演化，可能不适用。

第三种为固定步距发，顾名思义就是步距不变。设定步距d为一固定数值，从初始状态点　κ0处出发，不断迭代，直到　Π　（κ　i+　1）　＞Π　（κi），说明找到最靠近问题解的点，迭代结束。

由上述论述可知，要最快搜索到问题的解，关键是确定搜索方向和搜索步距。搜索方向必须是最速下降方向，搜索步距的选取比较多样。

其实梯度方向并不是搜索问题的唯一方向，如果将目标函数的曲率考虑进来，可以进一步提升搜索质量。由泰勒展开可知：

其中　∇Π　（κi）为讨论过得梯度矢量，　∇⊗∇Π　（κi）为Hessian对称正定矩阵。如果考虑了二次展开项，最速下降量修正为：

可见新的搜索方向需要求解　[　∇⊗∇Π　（κi　）]-1。这需要做一个逆运算，而逆运算在数值计算中是一个非常耗时而且不稳定的计算过程。所以需要寻找新的思路，避开　[　∇⊗∇Π　（κi　）]-1。

一种变通思路是采用[　∇⊗∇Π　（κi）]矩阵的共轭向量作为搜索方向。共轭向量符合以下条件：

令所搜改变量为：

如果要求β的选着，刚好得到裂缝反演系统的解，则代入目标函数二次展开公式，并求导可得：

求解，可求出β的解为：

这样就求出了最优的搜索步距向量：

搜索用到的共轭向量方向，并没有一个确定的选取规则。一般只要是Hessian矩阵的共轭向量即可。

确定了搜索方向，但还面临着裂缝反演问题中的一个重要障碍。虽然沿着共轭梯度方向可以找到局部最优解，但这个局部最优解不一定是全局最优解。尤其在裂缝反演问题中，虽然某一个参数空间的点iκ，周围的储层岩石模型和裂缝初始条件都不如　iκ点的模拟结果好，但这并不能保证这就是全部参数空间中，最接近答案的解。可能存在比　iκ点更接近真实储层属性性质的模型解。所以必须要给 “错误”留下一定的机会，这样可以帮助反演引擎跃出局部最优解，寻找更接近真实地质情况的解。这里，本次研究在共轭向量搜索的基础上，加入模拟退火方法，建立含时共轭退火反演方法。含时共轭模拟退火方法，就是在模拟退火模拟时，以Hessian矩阵共轭向量方向为搜索方向进行问题解搜索的反演方法，同时在每一步反演时，充分利用上一步反演的结果。

本书已经建立了裂缝反演系统　G （　X obs，ϖ0）=0，也分析了当初始参数为κ0时，如何确定搜索方向，找到最优解。但是对于裂缝反演问题，地质时间也是一个重要考量因素。如果每次确定完初始参数为　κ0，都进行一次从古到今的完整模拟，然后通过得到一个目标函数　Π　（κ0），然后利用共轭向量法确定搜索方向，再完整运行一次从古到今的裂缝演化过程，对计算机的要求非常高。所以，在每次确定初始参数为　κ0后，对每一个时间步内裂缝演化结果都应当和裂缝观察量做对比，新的参数搜索方向则按共轭向量法计算。以上就是含时共轭模拟退火方法的核心思想。

对于单一裂缝演化系统，采用统一的裂缝扩展规律G，则单步裂缝演化预测系统可以写为：

G i　（　X obs ）的模拟时间步长为Δt。

图49 裂缝扩展反演系统第i步模拟流程

这样，在确立裂缝扩展正向演化模拟模型后，在每一步裂缝扩展反演问题都转化为一个优化问题。并且在每一步模拟时均进行最优搜索。由于裂缝扩展演化系统属于非线性系统，所以反演会出现多个在局部最优解。模拟中采用了模拟退火技术[37-38]。模拟退火方法是通过模拟熔融金属冷却系统，寻找优化问题全局最优解的方法。物质随着温度降低，而逐渐冷却时日常现象，但其中却包含复杂的物理机理。如果冷却速度过快，物质内部可能出现亚玻璃态。Kirpatrik等提出，物质在冷却后完全变成晶体的状态时物质系统的能量最小状态，而亚玻璃态对应局部能量最小状态。可以看出，物质冷却过程过程中能量和裂缝反演系统中目标函数有着非常相似的性质。如果把裂缝反演系统，设想为一个物质冷却问题。而物质冷却过程中整个物质系统的能量设想为裂缝反演系统的目标函数，则如果选取适当的对应方法，则当物质冷却并完全形成晶体时，裂缝反演系统也可以越过局部目标函数最小解，找到全局最优解。所以，需要完整深入理解，物质冷却过程。以找多裂缝反演系统和物质冷却系统的对应关系。已经知道在物质冷却过程中，温度是一个重要控制因素，如果温度下降缓慢，则物质最终能全部变成晶体，如果温度下降过快，则会出现亚玻璃体。如果一个系统处于热力学平衡态，且温度为T，那么其能量分布将满足Boltzmann分布的形式：

其中Π是系统能量，k是Boltzmann常数。该分布表明系统处于高温时，各个状态出现的概率较为平均；系统处于低温时，高能状态出现的概率相对变小。在裂缝演化系统中，任意演化时刻时的系统能量为Π　i　（kj）。首先在本时间步内，从Π　i　（kj）出发开始搜索，新的参数点上目标函数能量为　Π　i　（　kj+1），则接纳该搜索点的概率为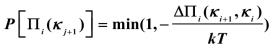 pagenumber_ebook=74,pagenumber_book=62 。如果　ΔΠ　i　（κ i　+1，κi ）＜0则接收新的搜索点，并继续搜索，否则以概率　exp　[　-ΔΠi　（κ i　+1，κi ）]接收新的搜索点。在向下一个时间步演化时，也同样计算目标函数能量，其中　ΔΠi+1　=Πi+1-Πi。即每一个时刻的系统能量依赖于两个时间点间的能量差值。裂缝反演系统是否接纳下一个模拟步的概率为 pagenumber_ebook=74,pagenumber_book=62 。如果　ΔΠi+1则接收第i步的裂缝扩展模拟结果，否则以概率　ΔΠi+1接收模拟结果，为了防止死循环，在每一个演化步内设定单步迭代上限　N*。如果单步迭代次数超过了　N*，则返回上一步进行修正。含时共轭退火反演系统模拟流程如图。

储层裂缝建模及多相流耦合理论研究成果

相关推荐