堆积形态与溃坝数值模拟分析

6.4.4.1　数值模拟方法

1.PFC3D颗粒流简介

PFC3D软件是由美国ITASCA公司开发的商用DEM软件，是模拟介质力学机理的良好工具。PFC3D主要从微观结构的角度出发，普遍适用于研究颗粒集合体的破裂、破裂发展和大位移的颗粒流问题，不断发展的PFC3D在胶结材料变形和流动过程，弹脆性介质损伤、断裂破坏过程等领域的研究也越来越具有独到的优势。

PFC3D继承了DEM的时步显示计算原理，处理对象只有两种基本单元：一是球形颗粒（ball）；二是墙面（wall），由facet组成。整个模型遵循牛顿运动定律，并用离散元法的力—位移关系来计算颗粒与颗粒及颗粒与墙体之间发生接触时的作用力。

PFC3D中的模型基于以下假设：①颗粒单元被视为刚性体；②颗粒间的接触在可忽略不计的点上；③颗粒间的接触视作柔性接触，颗粒允许在接触点上相互重叠；④重叠量与接触力大小有关，接触力通过力—位移定律计算，需要指出重叠量相比于颗粒尺寸非常小；⑤颗粒间的接触点可以存在连接（bonds）；⑥所有的颗粒的形状都是球形，也可以用到clump生成任意的形状，在每个clump中颗粒相互重叠但没有相互作用力。

该假设适用于岩土工程中的大部分散体材料，如砂土、粉土、岩石等，因为其变形主要是材料内部相对滑动，裂隙的张开或闭合产生，而不是由材料自身组成物质的变形所致。颗粒流更适用于模拟岩土体材料的力学性质。

除了颗粒单元，在PFC3D中还包括墙单元。墙单元上可以施加速度边界条件从而对颗粒进行压密。墙和颗粒之间同样通过接触产生作用力。墙单元不满足牛顿运动定律，不受力的作用的影响。在每个计算时步（timestep）内，依次利用力与位移法则更新模型中的接触力和运动法则更新模型中颗粒和墙的位置，直到达到平衡状态，计算过程如图6.4-5所示。

2.颗粒流接触本构模型

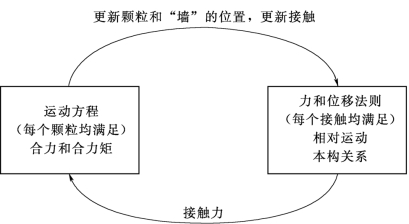
图6.4-5　PFC3D计算过程

颗粒流中材料的本构行为通过接触点上的本构模型来模拟。颗粒间的接触本构模型有3种：接触刚度模型、滑动模型和连接模型。滑动模型提供颗粒球间相对滑动时切向接触力和法向接触力之间的关系。连接模型提供了限制颗粒间的连接的法向力和切向力。

（1）接触刚度模型。接触刚度模型提供了接触力和相对位移间的弹性关系。PFC3D中提供两种接触刚度模型，简化的Hertz-Mindlin接触模型和线性接触模型。

（2）滑动模型。滑动模型是颗粒间在切向力的作用下发生滑动的判别标准。滑动模型无法向抗拉强度，在有接触连接存在时只有当接触连接破坏才会生效，由摩擦系数μ决定，颗粒间允许的最大切向力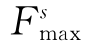为

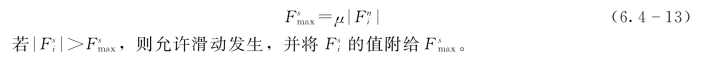
（3）连接模型。颗粒流中连接模型用于将接触的颗粒相互胶结在一起。只有颗粒与颗粒才能使用连接模型，颗粒与墙之间不能相互连接。PFC3D中有两种连接模型：接触连接模型和平行连接模型（图6.4-6）。

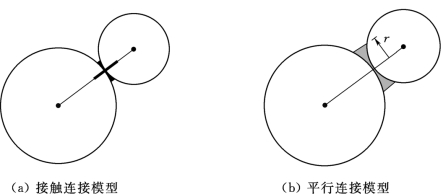
图6.4-6　连接模型示意图

1）接触连接模型：接触连接模型仅作用在颗粒间接触点上，只传递力不产生力矩，法向连接和切向连接共同决定了接触连接的强度。

2）平行连接模型：平行连接模型作用在以颗粒间接触点为中心的有限圆盘上。颗粒的相对运动将产生力和力矩。

3.阻尼本构

实际问题中，岩土体并非刚性体，系统的能量并不仅仅通过单元之间的摩擦方式进行耗散，颗粒与颗粒及颗粒与墙体之间的碰撞能耗也是系统能量损失的最重要途径之一。为了更真实地还原岩土体介质在运动过程中的碰撞问题，PFC3D提供了两类基本阻尼模型。

（1）局部阻尼。通过设定阻尼系数，可以给系统施加局部阻尼。该阻尼力被直接作用到颗粒单元的运动方程之中：

式中：分别为颗粒所受的外合力（包括重力）、质量和加速度；为局部阻尼力。

局部阻尼的存在显然不适用于滑坡在重力作用下的动力学分析，所以在本节的数值模拟中，阻尼系数统一设为零。

（2）黏性阻尼。黏性阻尼模型最早由Cundall提出，它的实际模型是一弹簧阻尼器。当黏性阻尼模型被激活，系统将在每个接触点处分别添加法向和切向阻尼器，用以耗散介质单元在碰撞过程中的法向和切向动能（图6.4-7）。

图6.4-7　黏性阻尼模型

对于考虑仅在重力场作用下的滑坡动力学问题，加入局部阻尼并不符合实际，所以在本章滑坡模型中局部阻尼统一设为零。运用颗粒自由下落的“碰撞—反弹”PFC3D模拟，考察模型中颗粒的速度恢复系数分析，确定了本节PFC3D计算模型统一的黏性阻尼系数分别为：法向阻尼系数为0.4；切向阻尼系数为0.1。

6.4.4.2　溃坝理论

堰塞坝作为自然作用的产物，其几何特征、物质组成和工作条件与人工土石坝具有明显不同。在坝体形态上，堰塞坝堆积体往往呈不规则形状，沿河流运动方向大多较人工坝长，且堰塞体内局部区域薄弱，坝顶凹凸不平，破坏一般首先在这些薄弱区域发生；在坝体结构上，因没有人工填筑过程，大部分堰塞坝结构松散，不均匀性强，堰塞体土石料的级配变化范围大，而且堰塞坝没有泄洪设施，当上游持续来水使得堰塞湖水位超过坝顶时，很可能导致堰塞坝发生漫顶溃决。据统计，绝大多数堰塞坝最终都将发生溃决，大约20%的堰塞坝在形成后1d内溃决，50%在10d内溃决，80%在6个月内溃决，90%在1年内溃决，一旦发生溃决，所产生的洪水或泥石流将对下游产生严重危害。因此，有必要研究堰塞坝漫顶溃决机理及溃决过程，为正确评估堰塞坝溃决致灾后果、科学制定堰塞坝溃决防洪应急预案提供技术支撑。

有学者根据55个溃决的堰塞湖坝体，分析堰塞湖坝体破坏主要有3种模式：漫顶溢流、潜蚀与管涌、坝坡失稳，其中坝顶溢流是最主要的破坏模式。这也得到了后来更多统计资料的认证，根据研究，在202个堰塞湖坝体破坏的案例中，有197个是因为坝顶溢流破坏，4个是因为管涌破坏，只有1个坝体是因坝坡失稳破坏。

土石坝渗透破坏可分为管涌和流土两种型式，管涌是指坝体中细颗粒在渗流作用下，从粗颗粒空隙中被带走或冲出的现象；流土是指渗流出逸坡降大于土体的允许坡降时，土石体表层被渗流顶托而浮动的现象。流土常发生在坝体下游或坝基的渗流出逸处，而不会在坝体内部发生。但不论是管涌或流土破坏，如未能及时发现并采取有效措施，最终都将在坝体或坝基内形成渗透通道，随着渗透通道的增大，其上部坝体厚度逐渐减小，当渗透通道上部坝体的重力超过坝体材料的抗剪强度后，通道以上坝体楔块将坍塌，坝顶高程逐渐降低，大坝将发生漫顶破坏而溃决。

南京水利科学研究院陈生水提出了合理描述渗透破坏溃口发展及溃坝洪水流量过程的数值模型和相应的数值计算方法，为更准确评估溃坝致灾后果，科学制定大坝溃决防洪应急预案，减轻因大坝溃决造成的损失提供技术支撑。

该理论方法首先是初始渗透通道的形成，随着渗透通道的扩大，通道以上坝体将发生坍塌，导致大坝发生漫顶破坏，水流从管流转化为堰流。

溃坝调查表明，由渗透破坏导致溃决的土石坝一般存在初始渗透通道。因此，本节采用南京水利科学研究院的土石坝渗透破坏溃决数学模型。假设初始渗透通道存在，筑坝材料平均粒径d50为土体颗粒代表粒径，通过分析土体颗粒在渗透通道中的受力情况，推导出渗透通道内坝体材料的临界起动流速，并分别建议了一种计算渗透通道扩展过程及大坝漫顶溃决后溃口发展过程的数值方法，同时采用管道流及堰流公式计算渗透通道扩展及大坝漫顶后溃口发展时的流量变化过程，并采用极限平衡方法对大坝漫顶后溃口边坡的间歇性失稳坍塌进行计算分析。

1.溃口流量

（1）渗透破坏。假设初始渗透通道为圆形，渗透通道中的水流速度可表示为

式中：μ为流速系数，此处取0.97；Δh为上游水库与渗透通道逸出点处的水位差。

当v＞vc时，土体颗粒起动，土石坝发生渗透破坏。需要说明的是，在水库库容较小且上游无水补给的情况下，渗漏使得水头Δh的明显减小，流速降低，渗透破坏可能会逐渐减弱甚至停止而使土石坝不发生溃决破坏；在水库库容较大或洪水期上游不断有来水补给的情况下，相对少量的渗漏将不可能使得水头Δh明显减小、流速显著降低，渗透破坏将会持续发展，进而导致土石坝的溃决。

考虑到可能导致土石坝发生溃决的渗透破坏，其渗透通道中的水流应为有压流，则通过渗透通道的流量可表示为

式中：Qb为通过渗透通道的流量；A为渗透通道的横截面积；R为渗透通道的半径。

（2）漫顶破坏。随着渗透通道的扩大，通道以上坝体将发生坍塌，导致大坝发生漫顶破坏，水流从管流转化为堰流。此后采用宽顶堰公式计算溃口流量。

式中：m为流量系数，此处取0.5；H为库水位高程；Hc为溃口底部高程。

库水位高程H的计算公式为

式中：H0为初始库水位高程。

溃口宽度B的计算公式为

式中：R为渗透通道坍塌时半径，且R=R0+ΔR，R0为初始渗透通道半径ΔHc=

溃口底部高程Hc的计算公式为

2.溃口冲蚀

（1）坝料颗粒起动流速。图6.4-8示意了土石坝发生渗透破坏时渗透通道中土体颗粒的受力情况。图6.4-9示意了土体颗粒在坝坡上的受力情况。对土体代表颗粒1而言，所受到的水流拖拽力为起动力，拖拽力可表示为

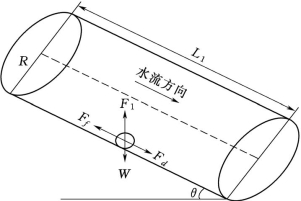
图6.4-8　土体颗粒在渗透通道中受力示意图

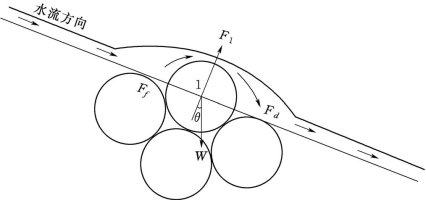
图6.4-9　土体颗粒在坝坡上的受力示意图

式中：Fd为水流对土体颗粒的拖拽力；Cd为拖拽力系数，一般取0.4；d50为土体颗粒粒径；γw为水的重度；v为水流流速。

土颗粒受到的上举力可表示为

式中：Fl为水流对土体颗粒的上举力；Cl为上举力系数，一般取0.1。

土体颗粒起动时受到的摩擦力可表示为

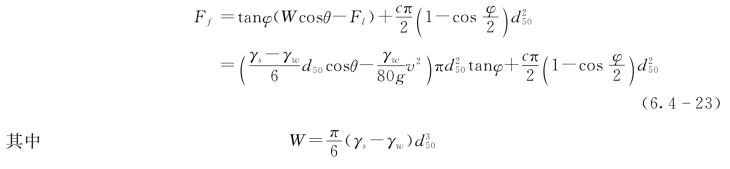
式中：Ff为土颗粒受到的摩擦力；φ为土颗粒间的内摩擦角；W为土颗粒的浮重度；θ为管涌通道倾角；c为土体的黏聚力；γs为土颗粒的重度。

通过受力分析可知，土颗粒1起动的临界条件为

将式（6.4-21）～式（6.4-23）代入式（6.4-24）可得到土体颗粒在坝坡上的临界起动流速：

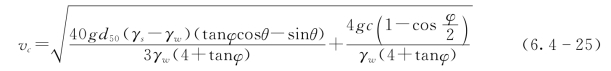
（2）冲蚀公式。渗透通道的发展过程与通道内土体所承受的水压力及坝体材料的物理力学性质有关。当初始渗透通道形成后，渗透通道的发展以冲蚀作用为主，陈生水建议了一个计算渗透通道内的土体单宽冲蚀率qs的表达式：

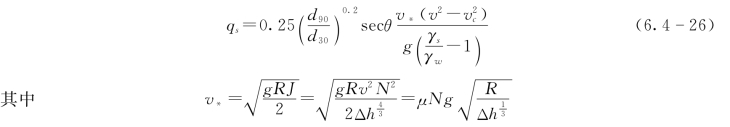
式中：d90和d30分别为小于它的颗粒含量占总重量的90%和30%的颗粒半径；v*为摩阻流速；v为水流流速；Δh为上游水库与渗透通道逸出点处的水位差；J为水流的水利梯度；R为渗透通道的半径；N为渗透通道的糙率半径。

则渗透通道内土体的冲蚀率可表示为

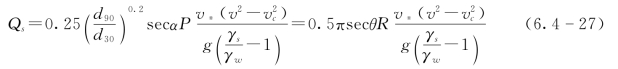
式中：Qs为土体冲蚀率；P为渗透通道的湿周。

随着渗透通道逐渐增大，通道上部坝体楔块将发生坍塌，渗透通道坍塌后，大坝发生漫顶破坏，水流从管流转化为堰流（图6.4-10、图6.4-11）。此后将采用下式计算此时坝体下游坝坡的冲蚀率。

图6.4-10　土石坝漫顶破坏溃口发展示意图

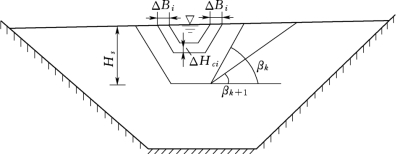
图6.4-11　土石坝漫顶破坏溃口发展示意图

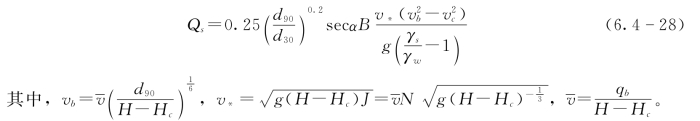
式中：α为土石坝下游坝坡坡脚；B为溃口宽度（假设初始溃口宽度为2R）。

3.溃口发展

时间段增量Δti内渗透通道半径增量为

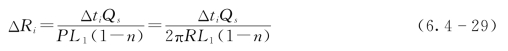
式中：n为筑坝材料的孔隙率。

时间段Δt内渗透通道半径增量为

随着渗透通道逐渐增大，通道上部坝体楔块将发生坍塌，渗透通道上部坝体将发生坍塌的条件如下：

式中：W为坍塌土体的重量；τf为崩塌楔形体两侧的抗剪强度；yc为崩塌楔形体的垂向尺寸，即坝顶高程与通道顶部高程之差。

此外，坍塌土体的重量W的计算公式为

崩塌楔形体的垂向尺寸yc（坝顶高程与通道顶部高程之差）的计算公式为

当渗透通道上部坝体发生坍塌后，坝体发生漫顶溃决，时间段增量Δti内水流下切深度增量为

式中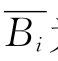：为溃口底部平均宽度；L2为坝顶及下游坝坡的长度；n为筑坝材料的孔隙率。

其中，溃口底部平均宽度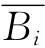的计算公式为

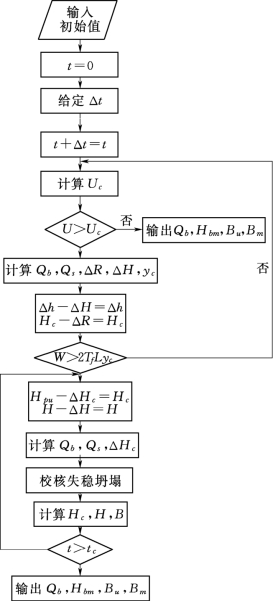
图6.4-12　土石坝渗透破坏溃坝过程数值模拟流程图

时间段Δt内水流下切深度增量为

如果不考虑溃口边坡失稳和坍塌引起的溃口横向扩展，溃口底部的冲蚀速率应该和溃口边坡的冲蚀速率大体相等，因此假定溃口的深度和宽度以相同的速率发展，则水流对坝体溃口两侧的直接冲刷形成的溃口宽度增量ΔB可表达为

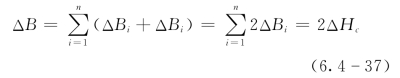
溃口受到水流的连续冲蚀发生垂向下切和横向扩展，边坡也随水流冲蚀变得越来越陡，当垂向下切深度达到临界深度时，溃口边坡发生间歇性失稳坍塌。临界深度可采用极限平衡方法导出

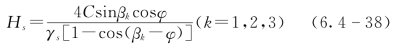
4.水库调洪计算

时间段Δt内水库水位变化量为

式中：Qin为入库流量；Sa为库水位为H时的水库面积。

5.数值模拟方法

通过时段迭代的计算方法来模拟土石坝渗透破坏溃决的溃口发展过程，具体求解过程见计算框图6.4-12。图中Hbm为溃口最终底高程，Bu为溃口最终顶宽，Bm为溃口最终底宽。

6.4.4.3　唐古栋堰塞坝参数反演

大量调查资料证实，土石坝因渗透破坏溃决的原因大体可以归纳为3种：因坝体本身缺陷导致的渗透破坏溃决，因坝基缺陷或其防渗措施缺陷导致的渗透破坏溃决以及因坝体与岸坡或水工建筑物接触部位的缺陷导致的渗透破坏。因此，初始渗透破坏的位置可以出现在库水位以下坝体的任何部位。

考虑到土石坝渗透破坏溃决过程具有明显的渐进性，不同的初始渗透破坏位置必然对其溃口发展规律、溃口流量过程以及溃坝洪峰流量具有重要影响，并进而影响到溃坝灾情。为此，以1967年唐古栋高速滑坡形成的堰塞坝为例，反演溃口发展规律、溃口流量过程以及溃坝洪峰流量，进而确定相应的初始渗透破坏位置。

根据唐古栋堰塞坝测量资料，简化得到坝体顺河向纵断面如图6.4-13所示。其中，唐古栋滑坡前缘初始河床水位高程为2370.00m，堰塞坝顶最低高程约2545.00m；现今河床高程为2390.00m；该处河床纵向坡度约为0.23°，河床底宽为200～300m，坝顶横截河床的宽度为500～800m，横断面呈倒梯形。溃坝分析所需其他参数见表6.4-6，假设初始渗透通道半径R0为0.1m。

图6.4-13　唐古栋老滑坡堰塞坝体简化纵断面（沿河床方向，单位：m）

表6.4-6　唐古栋滑坡漫顶溃决过程反演计算参数

注 d50为坝壳料的平均粒径；c为土体的黏聚力；φ为土体颗粒间的内摩擦角；γw为水的重度；γs为土颗粒的重度；B0为初始溃口宽度；d90为粒径小于它的颗粒含量占总重量的90%的颗粒粒径；d30为粒径小于它的颗粒含量占总重量的30%的颗粒粒径；L0为坝顶顺河床的宽度；n为筑坝材料的孔隙率；L2为坝顶及下游坡的长度；τf为崩塌楔形体两侧的抗剪强度；Qin为入库流量；Hpu为坝顶宽度内的最低点高程；θs为坝体的上游坡角；θx为坝体的下游坡角。

库水位为H时的水库面积Sa的计算公式为

因初始渗透通道位置的不同，渗透通道倾角及其相应反演计算参数亦有所不同，初步根据表6.4-7中倾角（θ）变化情况、取堰塞湖入库流量750m3/s（类比同时期同一地区流量）开展反演计算，得到结果见表6.4-8。

表6.4-7　唐古栋堰塞坝不同渗透通道倾角的计算参数

注 θ为渗透通道倾角；J为水流的水力梯度；N为渗透通道的糙率系数；L1为渗透通道的长度。渗透通道倾角1°时对应的初始垂向尺寸y0为149.86m，渗透通道倾角1.5°时对应的初始垂向尺寸y0为137.99m，渗透通道倾角2°时对应的初始垂向尺寸y0为126.55m。

表6.4-8　唐古栋堰塞坝反演初步计算结果

根据历史记载，唐古栋滑坡堵江后江水历时9d（192～216h）漫顶溃决，溃决时最大洪峰流量达到5.6万m3/s。因此，可以初步判定渗透通道倾角应在1°～1.5°之间，进一步根据表6.4-9中参数进行计算，所得结果见表6.4-10。

表6.4-9　唐古栋堰塞坝不同渗透通道倾角的计算参数

注 θ为渗透通道倾角；J为水流的水力梯度；N为渗透通道的糙率系数；L1为渗透通道的长度。渗透通道倾角1.1°时对应的初始垂向尺寸y0为147.45m，渗透通道倾角1.2°时对应的初始垂向尺寸y0为145.06m，渗透通道倾角1.3°时对应的初始垂向尺寸y0为142.68m，渗透通道倾角1.4°时对应的初始垂向尺寸y0为140.33m。

表6.4-10　唐古栋堰塞坝反演最终计算结果

经过进一步的试算，最终确定：初始渗透通道倾角为1.3°，相应的峰值流量出现时间为201h，最大洪峰流量达到5.6万m3/s；反演过程的流量变化曲线如图6.4-14所示。

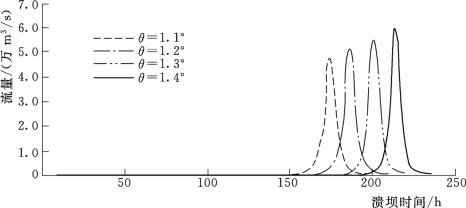
图6.4-14　唐古栋堰塞坝反演过程流量变化曲线

6.4.4.4　唐古栋滑坡堆积形态分析

经过先前对唐古栋滑坡的地质调查以及稳定性的分析，滑坡可能在极端情况下发生部分失稳的情况。运用基于离散元法的PFC3D软件，模拟该滑坡失稳时的运动堆积形态，并根据最终的堆积形态分析其对水电站所造成的影响。

1.模型建立

根据先前对唐古栋滑坡的地质调查及稳定性分析，滑坡失稳的主要物质来源区为A区的残余崩积物层和强松动岩层（图6.4-15），其中滑源区前缘最低高程为2475.00m，后缘最高高程在3500.00m，前后缘最大高差1025m，失稳方量约为1700万m3。

通过提取一定密度的高程点，运用三维地质建模，将每三个点组合成一个三角形墙面，最后将所有墙面有序连接。地形由19572个三角形组成，滑体由半径为3～5m的35109个球形单元组成（图6.4-16）。其中球与球之间设置平行连接，球与地表之间设置为接触刚度模型中的弹性模型。

图6.4-15　滑坡物质来源区

图6.4-16　唐古栋模型图

2.参数选取

PFC数值计算所需的参数一般不同于室内试验值或其他工程经验值，本节采取作法是运行PFC自带虚拟三轴测试程序进行参数标定与反演。与前面综合确定的参数进行对比，以反演确定计算需要的微观物理力学参数。

（1）根据实际方量与计算机计算能力确定颗粒最小半径为3m，最大颗粒与最小颗粒半径比为1.67。

（2）根据崩坡积物的变形参数弹性模量与泊松比反演出对应的方向刚度与切向刚度为106 N/m。

（3）采用平行连接模型模拟崩坡积物力学特性，根据强度参数黏聚力与内摩擦角反演出连接强度分别为法向强度20MPa、切向强度15MPa。

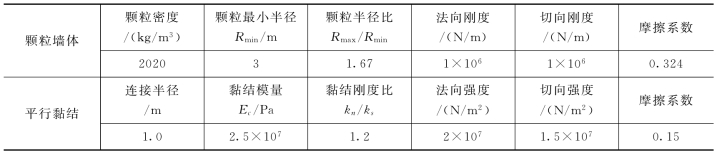
（4）颗粒摩擦系数会影响最后的堆积体形态，通过试算不同摩擦系数最终导致的堆积体形态，并与1967年唐古栋形成的堆积形态进行对比，摩擦系数的增加会导致最终堆积坝堆积坡度的增高，通过多次调整，最终得到相似堆积坝堆积坡度对应的摩擦系数0.324并使用于本次数值计算中。模型参数见表6.4-11。

表6.4-11　唐古栋滑坡PFC3D数值模拟参数

3.1967年堆积形态反演

现根据1967年唐古栋滑坡过程进行堆积形态反演，以验证上述模拟参数的可靠性。根据滑坡A区地形恢复唐古栋滑坡1967年以前的地形，并根据现在的地形确定1967年主要滑坡体的范围和方量，滑体范围主要在B、C、D区，方量约为9260万m3。现通过提取一定密度的高程点，运用三维地质建模，将每三个点组合成一个三角形墙面，最后将所有墙面有序连接。地形由18409个三角形组成，滑体由半径为3～5m的171343个球形单元组成（图6.4-17）。其中球与球之间设置平行连接，球与地表之间设置为接触刚度模型中的弹性模型。

图6.4-17　唐古栋1967年反演模型图

在模拟进行100000时步时，滑坡运动达到收敛平衡，堆积形态稳定。现分别沿河床截取一条横剖面线，沿着主滑方向截取一条纵剖面线（图6.4-18）。

图6.4-19为堆积高度最小的横剖面堆积形态示意图，从图中可以看出堆积体在A区下部河道内呈中部高两边低的梯形形态分布。堆积坝坝底宽为1483m，坝顶宽为516m，最大高度178m，下游坡度为18°，上游坡度为22°。

图6.4-18　唐古栋1967年反演最终堆积形态示意图

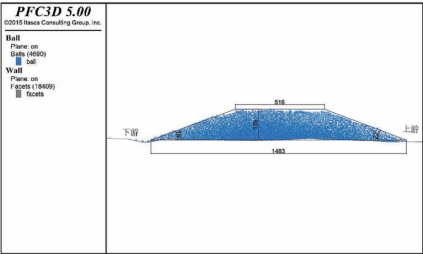
图6.4-19　唐古栋1967年反演横剖面堆积形态图

从图6.4-20可以看出，堆积体在滑坡对岸一侧堆积高度明显较高，在靠近滑坡一侧堆积高度较低，图中河谷中堆积体的最大高度为245m，最低高度为178m。经过反演得到的1967年唐古栋堆积形态与实际情况基本相符。

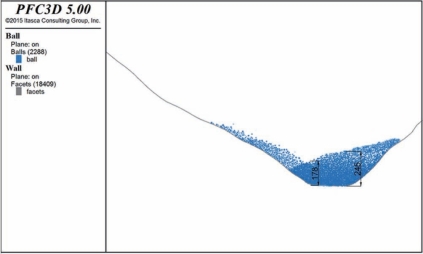
图6.4-20　唐古栋1967年反演纵剖面堆积形态图