西部水电工程滑坡灾变控制技术

5.1.1.1　滑移式失稳模式稳定性评价方法

1.极限平衡法之传递系数法

极限平衡法又称刚体极限平衡方法，极限平衡法是建立在莫尔—库仑破坏准则基础上的，它的基本特点是：只考虑土体处于破坏那一瞬间的静力平衡条件和莫尔—库仑准则，即求解边坡处于破坏那一瞬间的静力平衡方程组。当然在大多数情况下，静力平衡方程所涉及的未知数的个数都要大于方程的个数，因此，就必须对某些未知数做出假设，使方程组可解。

极限平衡法总体上可以分为两大类：一类是垂直条分法；另一类是滑移线法。两种方法的根本区别在于前者假定边坡破坏时只有在破裂面位置处于极限平衡状态，也就是假定只有破裂面处满足静力平衡条件和莫尔—库仑准则；而后者假定边坡破坏时，边坡内部全部处于极限平衡状态，处处满足静力平衡条件和莫尔—库仑准则。由于滑移线法的计算结果多数代表的是边坡稳定性状态的上限值，而垂直条分法的计算结果一般偏保守，因此，为安全起见，工程中一般多采用垂直条分的极限平衡法来评价边坡稳定性。报告中同时采用普通条分法、Janbu法、Bishop法和M-P法等4种常见的刚体极限平衡法，对各不稳定体进行了稳定性评价。其中，由于M-P法有概念清晰、适用范围广等优点，本书刚体极限平衡的稳定性计算将采用M-P法的计算结果为判断依据。

垂直条分的极限平衡法一般用于堆积层（包括土质）滑坡的稳定性计算与评价，其计算公式采用《滑坡防治工程设计与施工技术规范》（DZ/T 0219—2006）附录A.1的公式。

2.不同变形破坏模式的堆积层滑坡稳定性评价方法

（1）不同变形平衡模式滑坡渐进破坏过程。

1）牵引式滑坡渐进破坏过程。牵引式滑坡的坡脚是重要的阻滑段，经过人工开挖或者河流冲刷，加上持续降雨作用，滑坡前部首先变形，随着内外因素的进一步影响，滑坡由前至后逐步发生主动土压破裂，大主应力σ1主要为土体自重力，小主应力σ3为水平压应力，由于σ3的减小（前部失去支撑）而逐步产生主动土压破坏，破裂面与大主力σ1的夹角为45°-φ/2，φ为滑带的内摩擦角；到达一定程度时，滑坡主要表现为由下往上逐渐产生拉裂缝等现象，在一定时间内，滑坡后缘发生变形并伴随着牵引式滑坡整体破坏，表现为后退式渐进破坏过程。滑坡在整个演化过程中，在二维平面内一般只有一点处于峰值应力状态（即临界状态）。因此，牵引式滑坡在整个渐进演化过程中，滑坡体应力不断调整，塑性区逐步向后扩大，当某条块下滑力等于抗滑力时，该滑坡条块一般处于临界状态，处于该条块之前的条块为残余应力状态条块即发生剪切破坏，处于该条块之后的条块处于峰前应力状态条块即未发生剪切破坏，临界状态位置随着渐进破坏过程而逐渐向上移动（图5.1-1）。

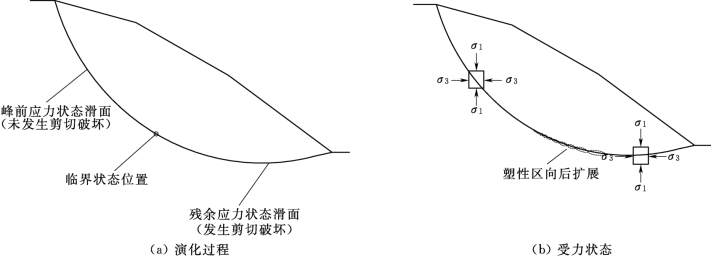
图5.1-1　牵引式滑坡渐进演化过程及受力图

2）推移式滑坡渐进破坏过程。推移式滑坡由于后缘常年的加载，后缘滑体荷载不断积累，加上降雨作用影响，触发了滑坡的变形，引起后部失稳始滑，一开始主要发生主动土压力破裂（受力同牵引式滑坡），滑坡后缘滑动带向下扩展，随着塑性区的扩大，应力集中范围向中前部扩大，滑坡中前部受平行滑面的下滑推力与滑面的阻滑力构成的一对力偶作用即受纯剪切力，派生出主压应力σ1和主张应力σ3（图5.1-2），在应力不断调整的过程中变形逐渐向前缘积累，滑坡主要表现为由后向前出现鼓胀、隆起等现象；随着时间的积累，滑坡前缘发生变形破坏并伴随着推移式滑坡整体变形破坏，表现为前进式渐进破坏过程。对于推移式滑坡来说，当某条块下滑力等于抗滑力时，该滑坡条块一般处于临界状态，处于该条块之前的条块为峰前应力状态条块即未发生剪切破坏，处于该条块之后的条块处于残余应力状态条块即发生剪切破坏；临界状态位置随着渐进破坏过程而逐渐向下移动，如图5.1-2所示。

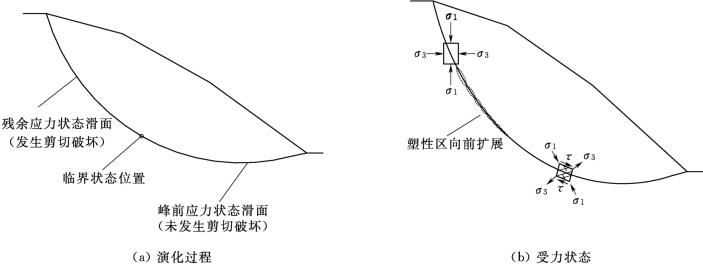
图5.1-2　推移式滑坡渐进演化过程及受力图

3）复合式滑坡渐进破坏过程。复合式滑坡同时具有牵引式滑坡和推移式滑坡的特点，变形始于前缘和后缘坡体，一开始前部和后部主要产生主动土压力破裂，引起后部失稳始滑以及前部关键阻滑段缺失，使得滑坡中部受平行滑面的下滑推力与自身的滑面阻滑力构成的一对力偶作用即受纯剪切力，派生出主压应力σ1和主张应力σ3（图5.1-3）而使中部出现滑动；随着时间的推移，滑坡前部和后部发生变形破坏，塑性区由前后逐步向中间扩展并伴随着复合式滑坡整体变形破坏，表现为由前后至中间的复合式渐进破坏过程。对于复合式滑坡来说，临界状态位置有两个，前部的临界条块定义为第一临界状态条块，后部的临界条块定义为第二临界状态条块，第一临界状态条块前部和第二临界状态条块后部的条块处于残余应力状态条块即发生剪切破坏，第一临界状态条块和第二临界状态条块之间的条块处于峰值应力状态条块即未发生剪切破坏；临界状态位置随着渐进破坏过程而逐渐由前后向中间移动，如图5.1-3所示。

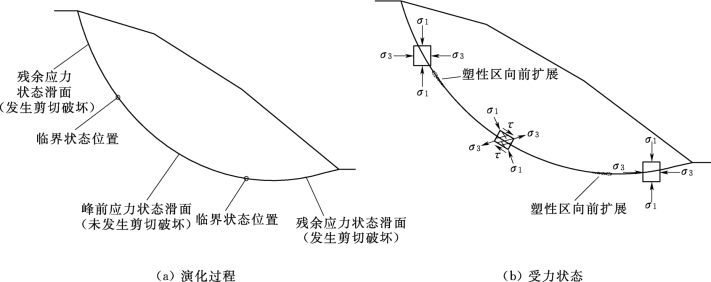
图5.1-3　复合式滑坡渐进演化过程及受力图

（2）滑坡稳定性计算模型的建立。通过对三种类型滑坡渐进性破坏的研究，在滑坡在演化过程的某一时刻进行条分，分为剪切和未剪切两段，并作如下假设：对于牵引式滑坡，假设总条块数为n，第m条块为临界状态条块（图5.1-4）；对于推移式滑坡，假设总条块数为n，第k条块为临界状态条块（图5.1-5）；对于复合式滑坡，假设总条块数为n，滑坡从上下开始发生剪切破坏，第m条块为第一临界状态条块，第k条块为第二临界状态条块（图5.1-6）。

图5.1-4　牵引式滑坡渐进破坏条分图

图5.1-5　推移式滑坡渐进破坏条分图

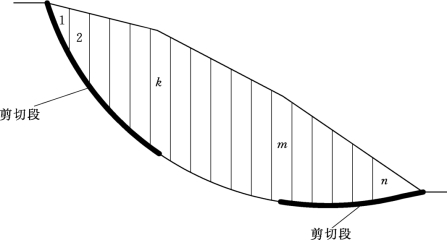
图5.1-6　复合式滑坡渐进破坏条分图

（3）滑坡稳定性计算公式建立和实现过程。滑坡的破坏是由局部破坏逐渐扩展贯通的渐进式过程，在该过程中，边坡的稳定性安全系数随着应力状态的调整而有所变化，在滑坡渐进破坏过程中其稳定系数计算须要结合滑带所处的状态，选择不同的抗剪强度参数，本文结合滑带本构特性和渐进演化过程，提供渐进破坏稳定性计算方法，反映了滑面不断发展的动态过程。由现有的稳定性计算公式，可以得到3种类型滑坡渐进破坏稳定性计算公式见表5.1-1。

表5.1-1　不同类型滑坡稳定性计算公式

注 Fs为稳定性系数；Ti为作用于第i条块上的下滑力，kN；Ni为作用于第i条块上的抗滑力，kN；φi为第i条块滑带土的内摩擦角，（°）；αi为第i条块滑面倾角，（°）。

由于传统边坡稳定性计算方法不能考虑土的抗剪能力与应变的相关性，这对于具有应变软化特性的土坡稳定性分析结果影响很大，整体计算时如采用峰值强度则偏于危险，而采用残余强度则过于安全。基于滑坡滑带渐进弱化的过程，滑带会出现应变软化现象，滑带从峰值抗剪强度逐渐衰减至残余抗剪强度，因此，在考虑渐进式演化过程计算滑坡稳定性时，提出滑带所处状态来选择强度参数，其中发生剪切贯通段取残余强度，未发生剪切贯通段取峰值强度，弥补了传统稳定性计算方法不能得到真实的应变软化滑坡稳定性系数的不足。

滑坡在渐进演化过程中，滑带在空间上呈现峰前应力、临界应力和残余应力等三种状态；为了更好地解释渐进破坏过程稳定性计算的过程，特以下进行阐述实现过程：

第一步，确定滑坡类型及临界状态条块：确定滑坡的变形破坏类型，通过对滑坡进行条分，进行不同类型滑坡在渐进破坏过程中临界状态条块的逐步确定。

第二步，滑带参数取值：确定临界条块后，对于牵引式滑坡渐进破坏过程稳定性计算时，临界条块前部的条块（m+1～n条块）参数取残余强度值，临界条块及其后部的条块（1～m条块）参数取峰值强度；对于推移式滑坡渐进破坏过程稳定性计算时，临界条块及其前部的条块（k～n条块）参数取峰值强度值，临界条块后部的条块（1～k-1条块）参数取残余强度；对于复合式滑坡渐进破坏过程稳定性计算时，第一临界状态条块前部和第二临界状态条块后部的条块（1～k-1条块和m+1～n条块）参数取残余强度值，第一临界状态条块及其后和第二临界状态条块及其前的条块（k～m条块）参数取峰值强度。

第三步，稳定性计算：采用表5.1-1中不同类型滑坡稳定性计算公式进行稳定性计算。因为滑坡渐进破坏过程中，滑带的参数是逐步弱化，临界状态位置不是固定不变的而是逐渐发生变化，即滑坡演化过程中的稳定性是动态变化的（但对于在某个时刻状态的稳定性系数为定值）。另外，在滑坡的稳定性评价时，我们更关注的是滑坡整体的稳定性，了解和分析滑坡现有的稳定性状态及未来的发展趋势；因此，计算滑坡稳定性时，需根据滑带弱化逐步求解计算而得到滑坡整体的稳定性变化曲线，以此通过不同类型滑坡的稳定性变化情况反映滑坡的稳定性状态，以及预测滑坡稳定性发展过程。

5.1.1.2　倾倒破坏模式稳定性评价方法

倾倒破坏是反倾岩质边坡的主要破坏模式。通过对层状反倾岩质边坡模型进行概化分析，将其看作一系列均质等厚的悬臂板模型，提出了反倾岩质边坡倾倒破坏模式稳定性评价方法。具体原理如下：

相邻板之间有相互作用力，因此其力学模型如图5.1-7所示。

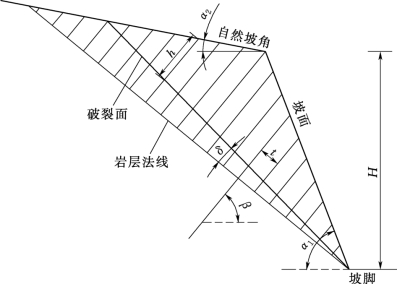
图5.1-7　岩质边坡倾倒破坏的地质力学模型

基于悬臂板理论及极限平衡理论在层状岩质边坡倾倒破坏中的应用，这些悬臂板在力的作用下会发生变形破坏，其破坏类型有拉破坏及剪破坏两种破坏模式。进一步分析边坡的破坏机制，发现倾倒体从坡顶到坡脚可以分为三个区域，即稳定区、拉破坏区和剪破坏区。此外，拉破坏区形成要早于剪破坏区。利用弹性理论中的悬臂板理论，根据图5.1-8，可以得出以单元层厚为基础的岩层受到的最小拉应力，其绝对值为

式中：y为悬臂板的厚度，m；N为轴向力，kN；M为弯矩，kN·m；I为横截面对中性轴的惯性矩，m4，即，其中b、t分别为悬臂板横截面的宽度和厚度，b均取单位宽度1m；A为悬臂板的横截面积，m2。

以单列悬臂板作为研究对象，作出该倾斜悬臂板在重力作用下的受力分析图如图5.1-9所示，则悬臂板受到的最小拉应力表达式如下：

图5.1-8　悬臂板拉应力求解图

式中：γ为悬臂板的重度，kN/m3；h为悬臂板的高度，m；t为单层悬臂板的厚度。

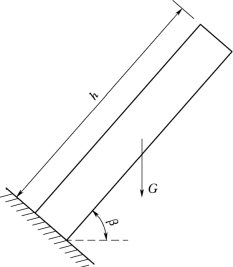
图5.1-9　悬臂板在自重作用下的受力分析图

在拉破坏区，悬臂板发生拉破坏的条件可以用下式表示：

式中：σt为悬臂板的抗拉强度。

联立公式（5.1-2）、式（5.1-3），可以得到重力作用下悬臂板的极限抗拉长度：

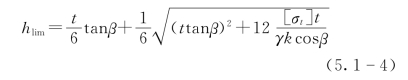
根据计算结果可知，当悬臂板在自重作用下产生拉破坏时，其长度应等于或大于极限抗拉长度。因此，假定某一列边坡岩层在自重力作用下第一个发生拉破坏，则其悬臂长度应该大于极限抗拉长度，且该列岩层产生的倾倒变形程度将大于相邻的上一列。一旦岩层发生拉破坏，就会与相邻的上列岩层分离，则此相邻两层之间没有相互作用力。而该列岩层之后的所有悬臂长度不小于极限抗拉长度的岩层，也将在第一个产生拉破坏岩层的基础上陆续发生拉破坏。最终，在第一列产生临界拉破坏的岩层之上的边坡岩层，由于其悬臂长度小于极限抗拉长度，因此将处于稳定状态。综上，位于拉破坏区之上的区域为稳定区，且悬臂长度为极限抗拉长度的岩层即为稳定区的最低边界。

根据现有分析，所有岩层的拉破坏都是基于最先产生拉破坏的岩层之后逐渐向边坡后部蔓延的，直至后部稳定区，此部分拉破坏区属于牵引式拉裂型；而紧邻最先产生拉破坏岩层的前部岩层，在自重及上部拉裂岩层的推动作用下，也可能产生拉破坏，直至拉应力小于岩块的抗拉强度。这部分拉破坏区属于推移式拉裂区。所以拉破坏区可以分为两个子区，即牵引式拉裂区和推移式拉裂区。拉裂区形成后，上下部岩体之间作用力将转化为沿拉裂面的剪切作用，并推动边坡前缘岩体产生剪切破坏，称之为前缘剪破坏区。拉破坏区的下边界岩层长度用hx表示。岩质边坡的倾倒破坏模式如图5.1-10所示。而滑面上各个区域的分布如图5.1-10所示。

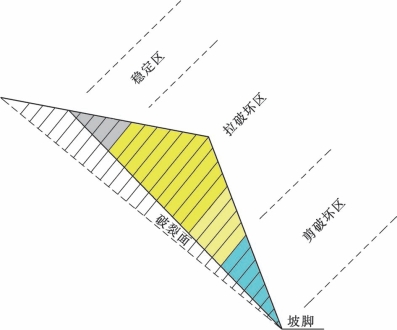
图5.1-10　岩质边坡弯曲倾倒模式

由图5.1-11可知，最长列岩层基准点O之后的滑面长度用lup表示，该列岩层基准点O之前的滑面长度用ldown表示，其计算公式如下：

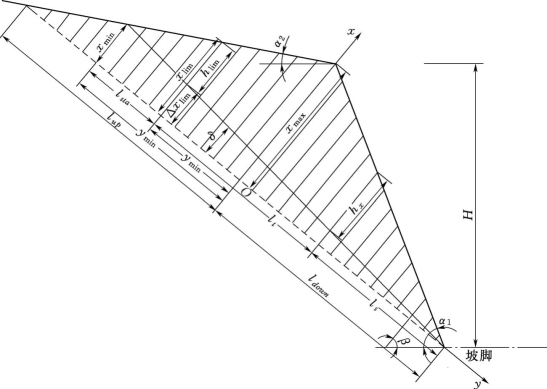
图5.1-11　岩质边坡弯曲倾倒破坏的地质力学计算模型

式中：xmax为顶部岩层的总长度，表示如下：

根据几何关系，我们可以得到以下方程：

式中：ylim和ymin分别为第一列长度为极限抗拉长度的临界破坏岩层的横坐标和破裂面与岩层自然坡面交点的横坐标。

根据式（5.1-7），ylim可表示为

联立式（5.1-8）和式（5.1-9），ymin可表示为

因此，滑面的稳定区长度lsta可以表示如下：

根据拉剪破坏区交界处的横坐标y，可以推导出拉破坏区的滑面长度lt和剪破坏区的滑面长度ls，其表达式如下：

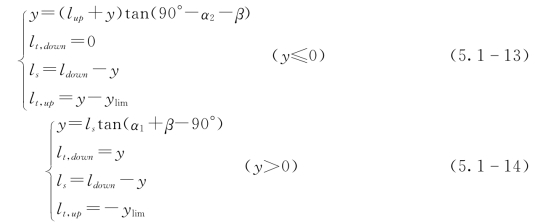
式中：lt，down为拉破坏区在基准点O之前的滑面长度；lt，up为拉破坏区在基准点O之后的滑面长度。

因此，拉破坏区和剪破坏区的重力可表示为如下两式：

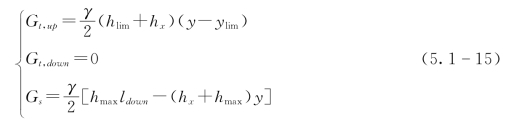
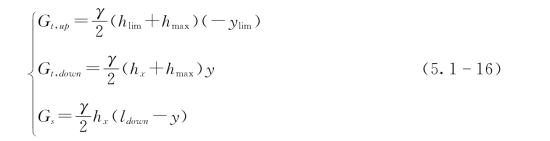
式中：Gt，up，Gt，down和Gs分别为最长列岩层之上和之下拉破坏区的重力以及剪破坏区的重力，kg。

稳定性系数是评价边坡稳定性的重要指标，而且它可以精确地描述边坡的破坏机制。基于以上边坡弯曲倾倒破坏机制的分析，提出了用极限平衡理论计算边坡稳定性系数的方法。图5.1-12为边坡倾倒破坏模式中拉破坏区和剪破坏区在自重作用下的受力分析图。

拉破坏发生后，假定拉破坏区的滑面、剪破坏区的滑面以及拉破坏区与剪破坏区之间的层间接触带服从莫尔—库仑准则。

对于发生拉破坏的岩层，假定其破坏面为图5.1-13中的形状。

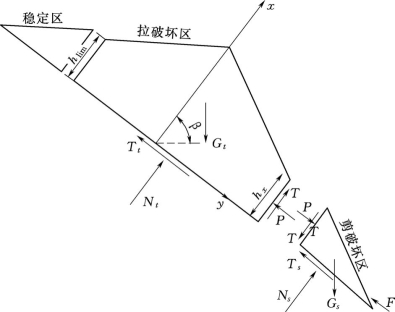
图5.1-12　倾倒破坏模式中拉破坏区和剪破坏区的受力分析图

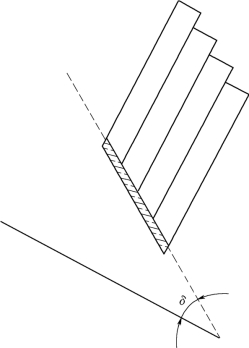
图5.1-13　弯曲倾倒破坏模式的破坏面模型

在拉破坏区，可得到如下静力平衡方程。

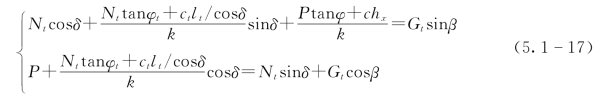
式中：Nt为拉破坏区岩层的轴向应力，kN；P为拉剪破坏区接触带间的正应力，kN；Gt为拉破坏区的重力，kN；c和φ分别为拉剪破坏区接触带间的黏聚力和内摩擦角；ct和φt分别为岩块的残余抗剪强度。

因此，根据式（5.1-17）可以推导出下式。

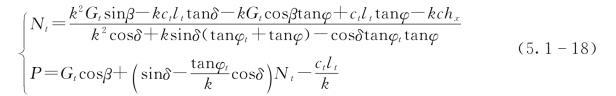
而在剪破坏区，其静力平衡方程可由下式表示：

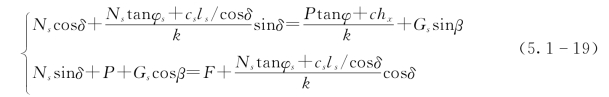
式中：Ns为剪破坏区岩层的轴向应力，kN；Gs为剪破坏区的重力，kN；F假定为作用于坡脚且平行于滑面的力，kN；cs和φs分别为岩块的峰值抗剪强度。

经整理，可以得到如下公式：

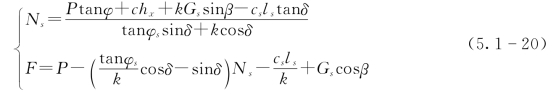
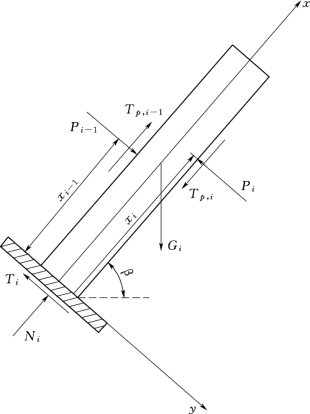
图5.1-14　拉破坏区下边界悬臂岩层的受力分析图

因此，拉剪破坏区接触带间的正应力及坡脚假设的力可通过式（5.1-18）及式（5.1-20）计算得到。

在公式计算中，k和hx是两个非常关键的参数，它们的值可以通过试算方法来确定。即先分别给定一个k和hx的初始值，根据计算可以得到相应的F值，因此必然存在一个k值，使得F恰好等于零，而此时的k值就是岩质边坡的真实稳定性系数。

拉破坏区下边界长度为hx的悬臂板的受力分析如图5.1-14所示。由图可知，对整体边坡而言，根据不同的hx值可以得到不同的稳定性系数，所以hx的真实值也是可以被确定的。如果先假定hx的初始值等于hlim，再通过Excel中的求解工具计算出当F等于0时的稳定性系数。此时，P、Nt和Ns的值便可通过式（5.1-18）及式（5.1-20）得到。进而再判断边坡岩层是否是在长度为hx的位置处产生了拉破坏。而对于该长度为hx的悬臂板，再次根据弹性理论中的悬臂板理论可得到如下公式：

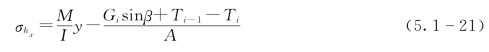
式中：Ti-1和Ti分别为长度为hx的悬臂板的上下表面受到的切向力；Gi为该列悬臂板的重力。

因此，根据以上公式可推导出该列悬臂岩层产生拉破坏的必要条件，即

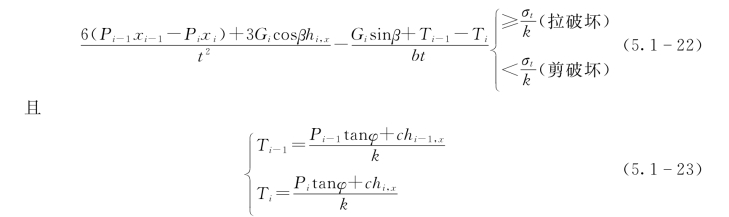
式中：Pi-1和Pi分别为长度为hx的悬臂板上下表面受到的法向力；xi-1和xi分别为该列悬臂板上下表面受到的法向力到基准点O的力臂，如图5.1-14所示。

根据式（5.1-13）和式（5.1-14），如果这一列发生拉破坏的悬臂板的长度hx被确定后，边坡拉破坏区的下边界将会下跌或上升。所以根据试算方法可以确定最终的hx值，同时该列岩层要满足式（5.1-22），而相邻的下一列岩层应满足式（5.1-23）。且式（5.1-22）和式（5.1-23）中的力臂也可以根据基准点O处的力矩平衡关系来确定。

由于重力场的影响，拉剪破坏区接触带间法向力的具体位置可按下式求出：

式中：η为比例系数，应位于0和1之间。

如果已知η，我们就可以根据式（5.1-22）和式（5.1-23）确定第i列岩层的失稳模式，也可以最终确定拉剪破坏区的边界。而且，倾倒边坡的稳定性系数也可按式（5.1-20）计算得出。

地震是触发边坡失稳的一个重要因素，在稳定性计算中如何科学的考虑地震力作用显得尤为重要。地震作用下，单列悬臂岩层在自重及地震力作用下的受力分析如图5.1-15所示，则该列岩层受到的最小拉应力表达式如下：

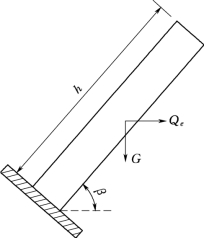
图5.1-15　悬臂板在自重及地震力作用下的受力分析图

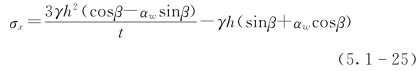
式中：αw为边坡综合水平地震系数。

因此，可进一步得出自重及地震力作用下悬臂岩层的极限抗拉长度：

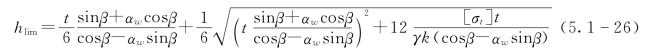
边坡整体在自重及地震力作用下的受力如图5.1-16所示：

拉破坏区的静力平衡方程如下：

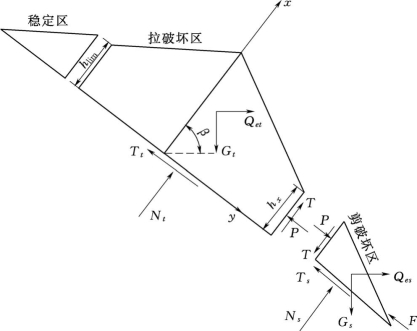
图5.1-16　地震作用下倾倒破坏中拉破坏区和剪破坏区的受力分析图

拉破坏区下边界长度为hx的悬臂岩层在地震作用下的受力分析如图5.1-17所示。该列悬臂岩层的最小拉应力为

因此，该列岩层产生拉破坏的必要条件为

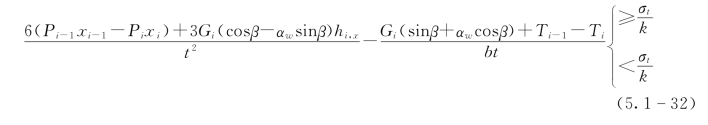
图5.1-17　地震作用下拉破坏区下边界悬臂岩层的受力分析图

且

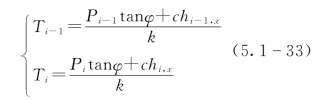
如上所述，该方法不仅可以计算倾倒边坡的稳定性系数，也可以划分稳定区、拉破坏区和剪破坏区三个区域的范围。