JB/T 5314—2002滚动轴承振动(加速度)测量方法 此标准规定了公称内径3~120mm的深沟球轴承、角接触球轴承、圆锥滚子轴承和圆柱滚子轴承的振动(加速度)测量方法。内径10~120mm的轴承振动测量应符合JB/T 5313的规定。......
2025-09-29
振动特性包括系统的固有特性(固有频率、振型、阻尼比)和动力响应特性。可以单项测试,也可各项同时测试;可在现场实测,也可在实验室进行更详细的试验分析和作模型试验。
(1)固有频率的测试
1)敲击法。敲击试件,使试件产生能够进行测量的自由振动,记录下自由振动的时间历程与时标比较,便可算出试件的固有频率。设备简单、方便迅速,但只能测出试件少数低阶固有频率。
2)共振法。对试件进行频率扫描激振,记下频率响应曲线,即可定出各阶谐振点及固有频率。
3)谱分析法。对试件进行随机激振或瞬态激振,获取振动信号,经过信号分析仪得到功率谱或幅值谱,由谱图中的尖峰分量确定固有频率。
4)试验模态分析法。对试件进行正弦、随机或瞬态激振,获取试件传递函数数据。使用频域数字曲线拟合法或时域数字拟合法,对系统动力学模型进行优化识别,快速而准确地同时将系统的固有频率、阻尼比和振型一起测识出来。这种方法得到的固有频率十分准确,并且还可以识别出频率十分接近的密集模态,排除虚假峰值频率。
(2)振型的测定 振型的测定常与固有频率的测定同时进行。根据结构的形状、尺寸选用以下方法。
1)探针法。激振试件,使它处于谐振状态,然后用探针依次接触试件上各点来探测节线位置,找出节线后即可定出振型。
2)沙型法。在平板的试件表面洒上细砂粒;激振试件,使它处于谐振状态,砂粒将逐渐移动和集中到节线附近,显示出节线的位置和形状,从而定出振型。
3)传感器测定法。在试件上选择数量足够的测振点,并定出各点的坐标。激振试件,使他处于谐振状态,用传感器和测振仪测出各点的振幅(或加速度)和相位,即可绘出其振型。此法适用于测定复杂、大型及刚度较大的构件或机器。测试时注意传感器的附加质量不会对试件原来的振动状态有较大的影响,并注意其他振型的影响,应选用多点激振的方式。
4)谱分析法。对被测试件各测振点振动位移响应数据进行幅值谱、功率谱和互谱分析。幅值谱可以给出各个测振点在各频率点上相应的幅值大小;互谱则可建立起各测振点间的相互关系,从而确定各阶振型。
5)试验模态分析法。如前所述,试验模态分析法既可测固有频率,又可测阻尼比及振型等各模态参数,是当前准确、快速、方便和实用范围广的方法。在一些具有模态分析功能的现代振动信号处理系统上,所分析的振型结果,可直接在荧光屏幕上进行立体振型动态活化显示,并绘图输出。
6)激光全息照相法。有时间平均法,频闪法和实时法三种。时间平均法操作简单,用得较多,其光路布置见图7-19。它的原理与静止物体立体全息照相的不同点是:物体在全息干板曝光过程中作稳定的简谐振动,故得到物体的时间平均全息图。当这种全息图再现时,物体的全息照片上有明暗相间的干涉条纹,这种条纹图就是物体的振型图。
由于曝光时间较长,试件振动必须稳定,不应受其他振动的干扰,故试验必须在防振台上进行,一般激振设备都不适用。常用压电元件激振法,即将压电片粘贴在试件易激起振动的部位,由音频信号发生器和功率放大器激振。此法适用于高频情况,激振频率由数百Hz到数万Hz;但在低频情况下,压电片阻抗太大,不易与功率放大器匹配,不宜采用。
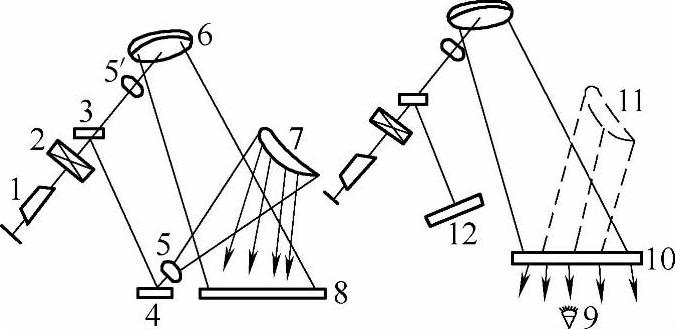
图7-19 激光全息照相的光路布置
1—氦-氖激光管 2—快门 3—分光镜 4—平面反射镜 5、5′—扩散镜(显微镜物镜) 6—球面反射镜 7—物体(叶片) 8—全息干板 9—观察点 10—全息照像 11—物体的全息像 12—不透明挡板
(3)阻尼比的测定 除了上述试验模态分析方法外,常用的还有以下方法:
1)自由振动法。激振试件进行自由振动,将其振动衰减波记录下来(见图7-20),量取第一个波的峰值A0及随后第n个波的峰值An,按下式计算出阻尼比ζ。

其中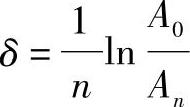
当ζ≤0.1时
2)受迫振动法。对试件进行频率扫描激振,记录其各阶共振峰附近的波形(见图7-21),当阻尼比ζ较小(ζ≤0.1)时,按下式计算其阻尼比:

式中,fn为共振频率,共振振幅为A0;f1、f2为振幅为0.707A0时的频率。(https://www.chuimin.cn)
若相邻两共振峰靠得很近,则用试验模态分析法可获得较准确的结果。
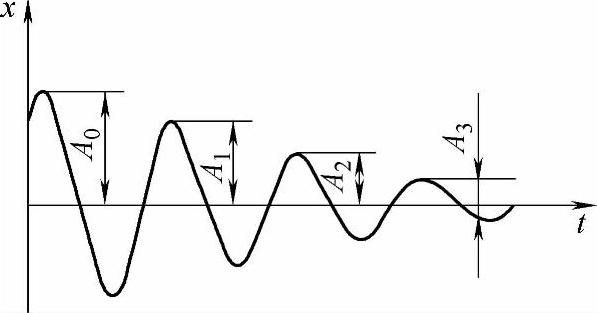
图7-20 自由振动衰减波
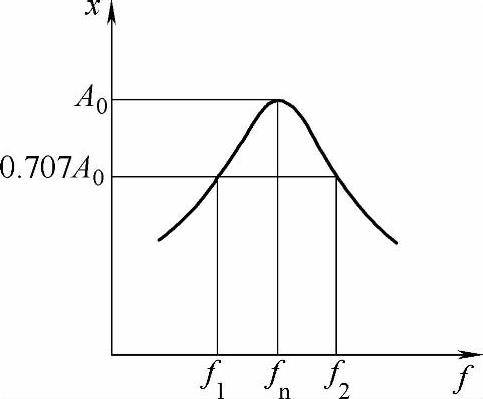
图7-21 共振波形
(4)动力响应特性的测试 对机械动力系统施加激振力(输入),测量出系统的振动响应(输出),对系统进行以下分析计算:已知输入和输出,识别出系统的固有特性(固有频率、振型、阻尼比、刚度、质量);已知输入和固有特性,计算出系统的动力响应;已知输出和固有特性,识别出系统的输入特性。
通常用输入和输出之间的关系-传递函数,来描述系统的动力响应特性,其测试过程如下:①在选定坐标点和所需频率范围内,对测试对象施加一定类型(简谐、瞬态或随机激振)和量级的激振力。②测量激振力和所需坐标点的振动响应,或测量输入、输出的互谱及自谱密度函数。③对测得的激振力和响应信号,或互谱及自谱密度函数进行分析处理,求出对应各激振频率的传递函数数据。④将测得的传递函数数据,根据需要以各种图形(如幅频、相频或幅相特性图),或数据的形式进行记录而输出。
图7-22为典型的模拟式传递函数测试系统框图,图7-23为典型的数字式传递函数测试系统框图。
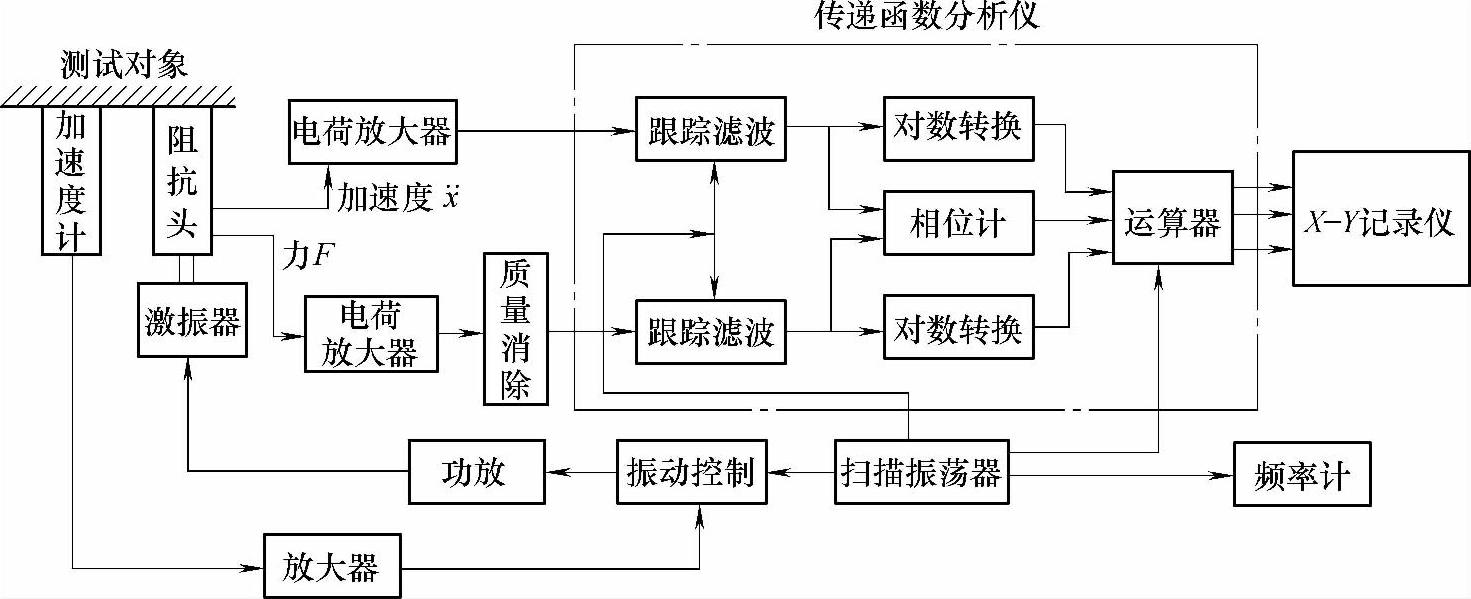
图7-22 典型的模拟式传递函数测试系统框图
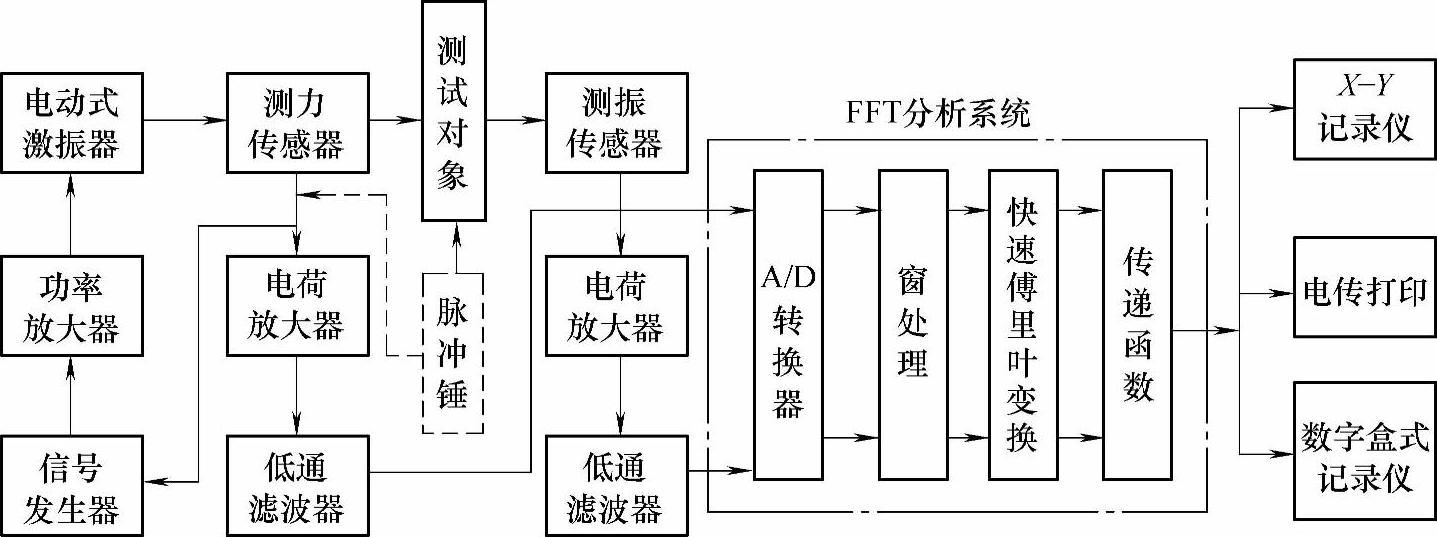
图7-23 典型的数字式传递函数测试系统框图
(5)模型试验 对于大型复杂的机器,宜利用模型试验来确定其振动特性。特别是在设计新产品时,通过模型试验,可以验证理论分析是否正确,获得设计所需的资料,模型可制成机械模型或电模型。
机械模型用得较多的是几何相似的模型,即模型的各尺寸与实物的相应尺寸都成一定比例。以δ表示实物某参数与模型同一参数的比例系数,设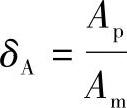 ,
,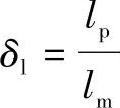 ,δF=
,δF=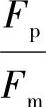 ,
,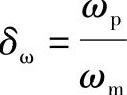 ,
,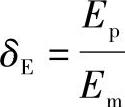 ,
,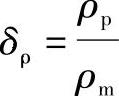 ,
,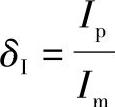 ,
,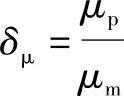 ,
,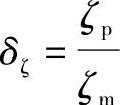 ,…分别代表实物与模型的振幅比,尺寸比,激振力比,频率比,材料弹性模量比,材料密度比,截面惯性矩比,泊桑比的比例系数,阻尼比的比例系数,……。其中,下标p代表实物,下标m代表模型。弯曲振动时,考虑动刚度相似和几何相似的准则,得
,…分别代表实物与模型的振幅比,尺寸比,激振力比,频率比,材料弹性模量比,材料密度比,截面惯性矩比,泊桑比的比例系数,阻尼比的比例系数,……。其中,下标p代表实物,下标m代表模型。弯曲振动时,考虑动刚度相似和几何相似的准则,得

扭转振动时,F代表激振力矩,A代表角振幅,并把弹性模量E换成剪切弹性模量G,截面惯性矩I换成极惯性矩Iρ,仍可使用式(7-35)为其相似准则。如果实物与模型的材料不同,其泊桑比不同,即δμ≠1,则需修改式中的δF和δω为
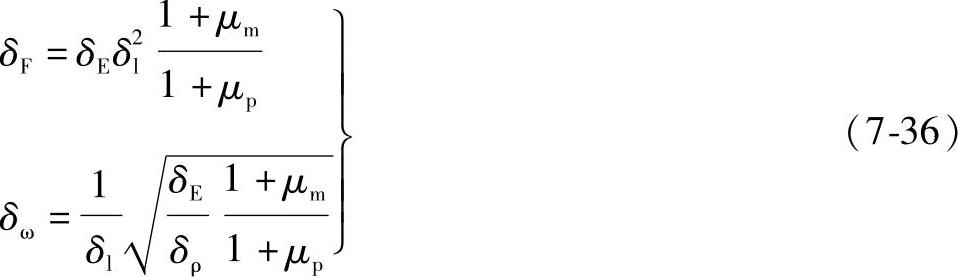
通常都希望模型比实物小,即δl>1,故模型的固有频率比实物的固有频率高出几倍甚至几十倍。如果给试验带来困难时,则放弃几何相似,而采用其他相似条件,例如采用运动相似。此时模拟条件应在理论分析的基础上按相似理论求出。
对于多自由度系统,其运动相似的模拟条件是:模型与实际系统各相应参数间的比例相同,即
1)模型的各质量与实际系统的相应质量之比相同,质量的比例系数为δm。
2)模型中各质量处的刚度与实际系统中相应处的刚度之比相同,刚度的比例系数为δk。
3)模型与实际系统的阻尼情况相同。当不考虑阻尼时,实际系统与模型的固有频率之比δω为

相关文章

JB/T 5314—2002滚动轴承振动(加速度)测量方法 此标准规定了公称内径3~120mm的深沟球轴承、角接触球轴承、圆锥滚子轴承和圆柱滚子轴承的振动(加速度)测量方法。内径10~120mm的轴承振动测量应符合JB/T 5313的规定。......
2025-09-29

2.机械振动测试内容机械振动测试是研究和解决工程技术中许多动力学问题的必要手段,机械振动测试内容根据使用目的不同可分为两类:振动基本参数的测量 即测量机电设备或结构在工作状态下振动的各种参数,如振动位移、速度、加速度、频率和相位等,其目的是了解被测对象的振动状态,评定被测对象振动强度和等级,了解结构件动载荷及动变形,寻找振源及传递路径,对设备运行状况或结构健康状况进行监测、分析、诊断和预测。......
2025-09-29

因为当凸轮工作在高速时,3-4-5 多项式轮廓将被压缩,这使其低通滤波特性被减弱。图7.6 比较了在操作转速附近由光滑后的凸轮轮廓引起的振动和由标准3-4-5多项式凸轮轮廓引起的振动的振幅。保持系统的自然振动周期不变,速比的降低意味着转速的升高。结果暗示着在如图7.6 所示的速度范围内,与标准的3-4-5轮廓相比,光滑后的凸轮轮廓将振动抑制到了一个很小的范围内。图7.6速比变化情况下的残余振幅......
2025-09-29

管道振动响应测试系统框图如图10-40 所示。振动响应信号采集振动时域信号能够反映振动信号幅值大小及其随时间的变化情况。图10-41管线振动响应测试点分布图图10-42测点1 在Z 方向的响应频谱图振动响应信号分析①不平衡惯性力和管内流体的压力脉动在异形管件等处产生的激振力是管线振动的两个主要原因。②注水泵出水管线振动的两个主导频率为29 Hz 和30.5 Hz,分别对应于泵房内基础激励频率和管线内流体压力脉动频率。......
2025-09-29

图3-26触头接通时的机械振动除触头本身的碰撞外,电磁机构中衔铁与铁芯接触时的撞击以及短路电流通过触头时产生的巨大电动斥力,均可能引起触头振动。如图3-27所示,在接通过程中动触头以速度v1朝静触头运动,并于t=t1时与之相撞。碰撞后,触头接触面上将发生弹性及塑性形变。动触头具有的动能一部分消耗于接触面的摩擦和塑性形变,其余部分则转化为弹性形变势能。......
2025-09-29

通过分析可以看出,异步电动机带恒转矩负载的降压调速实际上是靠增大转差率、减小输出功率来换取转速的降低的。如果增大转子电阻,临界转差率将加大,可以扩大恒转矩负载下的调速范围,并使电动机能在较低转速下运行而不至于过热,这种高转子电阻电动机又称作交流力矩电动机,这种电动机的降压调速机械特性如图5-6所示,虽然调速范围变大了,但是缺点是机械特性较软。......
2025-09-29

干扰力消除,强迫振动停止。自激振动(颤振)机械加工过程中,在没有周期性外力的作用下,由系统内部激发反馈产生的周期性振动。自激振动的频率等于或接近于系统的固有频率。自激振动能否产生及其振幅的大小,决定于每一振动周期内系统所获得的能量与系统阻尼消耗的能量的对比情况。......
2025-09-29

PCP每次均将数据集随机分成2个子集,轮流作为训练集与测试集,得到2个测试精度,10次均值实际上是20个精度值的平均,这个均值的有效性更好。交叉检验实验说明,利用特征数据能较好地区分各类行为。按第5.3.2节向量分量排列顺序,分量下标为k的特征,如果k或k+1能被4整除,说明其反映的是空档变化情况;不符合这个特征,说明其反映的是宽度变化情况。......
2025-09-29
相关推荐