图7-20 微电机的定子片和转子片2.排样设计由于微电机的定子片和转子片年产量大,故适宜采用多工位级进模冲压,该制件的冲压工序均为冲孔和落料。工位③的落料凸模上均布了3个顶杆,目的是使凸模上的导正销与落料的转子片分离,阻止转子片随凸模上升。......
2025-09-29
在讨论单圆盘转子的振动中,是假定转子的质量集中在圆盘上,而略去了轴的质量。这样,只用一个独立坐标就可以完全描述转子在某个方向的运动,因此称为单自由度系统。在实际中,当转子只有一个叶轮而轴又较细时,就可以这样处理。但是,当不满足这个条件,就不能处理成单自由度系统,而必须处理成多自由度系统。其简化的力学模型就是有多个集中质量(由叶轮、轴套及轴段等简化而来)。相邻集中质量间,由无质量的弹性轴段连接,各轴段的刚度就是原来轴段的实际刚度。因为连接轴段是有弹性的,因此集中质量受力运动后,相互之间必有相对位移。这样要描述集中质量在转子横向振动过程中的任意瞬时位置,每个集中质量都需要一个独立坐标系。如果描述三个集中质量的横向运动,就要三个独立坐标,称为三自由度系统;假如系统有N个集中质量,就需要N个独立坐标来确定各质点的瞬时位置,故称为N自由度系统。
(1)二自由度转子系统的自由振动 见图7-6,转子的质量都集中在1和2两点,每点质量都等于m0,转子两端支承在相同的短轴承上,轴为均匀等直径轴,截面惯性矩为I,弹性模量为E,轴长为l,两集中质量分别位于距两端轴承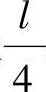 处。
处。
为了研究转子的横向弯曲振动,即图示在y方向的振动,取二集中质量在y方向的坐标为y1(t),y2(t),这两个坐标随时间变化的规律,就是整个转子在y方向的振动规律。
由于转子作无阻尼的自由振动,因此振动中仍然是惯性与弹性力相平衡,设1和2两点的振动位移分别为y1、y2,则可列出振动微分方程组为

式中,aij是影响系数。其物理意义是:在j点作用有单位力时引起的i点的位移,比如a11就是在1点作用有单位力时引起的1点的位移。可见式(7-13)本质上是惯性力与弹性力之间的平衡。
对图7-6所示的转子,可以求得
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
要发生振动,表示式(7-13)的解存在,此时就可将式(7-13)整理成式(7-14):
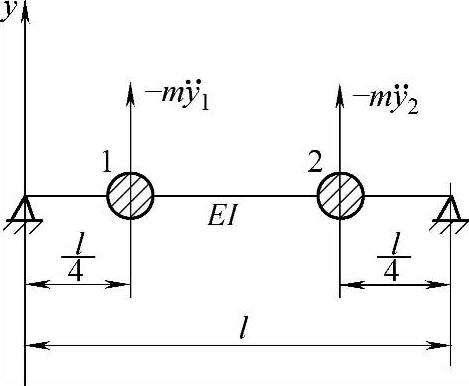
图7-6 二自由度转子
m2(a11a22-a212)ω4-m(a11+a22)ω2+1=0 (7-14)
因此该转子发生自由振动的频率值,必定是上面方程的根。解频率方程,可得到两个频率值:
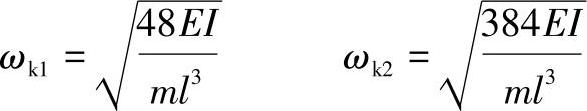
可见对二自由度系统,存在着两个固有频率,即两个临界转速。以大小排列,ωk1称为第一阶固有频率,ωk2称为第二阶固有频率。
相关文章

图7-20 微电机的定子片和转子片2.排样设计由于微电机的定子片和转子片年产量大,故适宜采用多工位级进模冲压,该制件的冲压工序均为冲孔和落料。工位③的落料凸模上均布了3个顶杆,目的是使凸模上的导正销与落料的转子片分离,阻止转子片随凸模上升。......
2025-09-29

当SEq<0时,特征值p1、p2为两个实数,其中一个为正实数,所以电力系统受扰动后,功角偏差Δδ最终以指数曲线的形式随时间不断增大,因此系统是不稳定的。这种丧失稳定的形式称为非周期性地失去同步。称为实用判据,常被应用于简单电力系统和一些定性分析的实用计算中。在稳定工作范围内,自由振荡的频率为图14-2fe、SEq随δ的变化这个频率通常又称为固有振荡频率。......
2025-09-29

考虑到切断面为定子片外侧的非工作部位,不影响其使用,所以采用了单面切断的方式。小电机定、转子片套冲多工位级进模结构如图7-19所示。......
2025-09-29

物体表面积的大小与物体的尺寸成反比,纳米纤维的直径达到纳米级,其表面积大大增加,并且由于纳米纤维易与其他原子结合,显示出较强的活性。纳米纤维优异的特性使其在航天材料、化工、医药等工业生产方面拥有巨大的应用价值。纳米纤维的应用价值巨大,在纺织成品中加入纳米材料,能够形成一层特有的薄膜。此外,纳米纤维还可用在工业产品的精炼方面。纳米纤维因其独特的优良特性,一直都受到各个国家科学家的青睐。......
2025-09-29

在多工位级进模中,垫板可分为固定板垫板、卸料板垫板和下模板垫板三类。固定板垫板承受凸模的作用力,保证弹簧有足够的压缩行程;卸料板垫板承受卸料组件和卸料板镶块的冲击载荷;下模板垫板承受凹模或凹模镶件的作用力。通常在多工位级进模设计中为了安全可靠,一般都设置有垫板的模具结构。垫板的厚度一般取8~18mm。对于分段式垫板,厚度尺寸要保持一致。......
2025-09-29

几何相似 这是指模型与实物的几何形状相同,对应的线性长度比为一定值,对应角度相等。几何相似是运动相似的先决条件。根据气体流动的气动热力过程及能量传递过程的相似要求,两个通风机的气流过程相似条件可归结如下:几何相似、叶片进口的速度三角形相似、雷诺数相等。下面将证明只要满足上述相似条件,两个通风机一定是相似的。......
2025-09-30

转子绕组接地是发电机运行中较易发生的故障,又是严重影响发电机安全运行的故障。近几年来,国内大型发电机由转子绕组接地所引起的严重运行事故并不少见。因此研究转子绕组接地的原因和防止措施具有重要实际意义。分析认为,接地的原因是制造质量不良、转子绕组受潮。经检查,发电机转子汽侧#9 槽及励侧#15槽口处各有一点接地,形成两点接地故障。......
2025-09-29

流线能够形象地给出流场的流动状态。流线的引入是欧拉法的研究特点。2)通过某一空间点在给定瞬间只能有一条流线,一般情况流线不能相交和分支。4)流线密集的地方,表示流场中该处的流速较大;稀疏的地方,表示该处的流速较小。图2-2 流线图从图中看出,流线分布的疏密度与流体横断面积的大小有关。横断面积小的地方流线密,流速大;横断面积大的地方流线疏,流速小。流线的形状和固体边界的形状有关。......
2025-09-30
相关推荐