当SEq<0时,特征值p1、p2为两个实数,其中一个为正实数,所以电力系统受扰动后,功角偏差Δδ最终以指数曲线的形式随时间不断增大,因此系统是不稳定的。这种丧失稳定的形式称为非周期性地失去同步。称为实用判据,常被应用于简单电力系统和一些定性分析的实用计算中。在稳定工作范围内,自由振荡的频率为图14-2fe、SEq随δ的变化这个频率通常又称为固有振荡频率。......
2025-09-29
(1)无阻尼自由振动 图7-1所示为对称单圆盘转子。假设圆盘质量为m,位于两支承中间,并且轴很细,其质量相对圆盘来说甚小,可以略去不计。这样整个转子的质量m集中在圆盘中心s点上,成为一个最简单的对称单圆盘转子。以跨距中点O为原点,取直角坐标系xOz。
设轴中点处的刚性系数为K(使轴产生单位长度的位移所需的力)。此转子在受到扰动后,就要以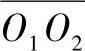 线为平衡位置发生自由振动。由惯性力与弹性力相平衡,得运动微分方程式为
线为平衡位置发生自由振动。由惯性力与弹性力相平衡,得运动微分方程式为
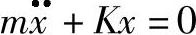
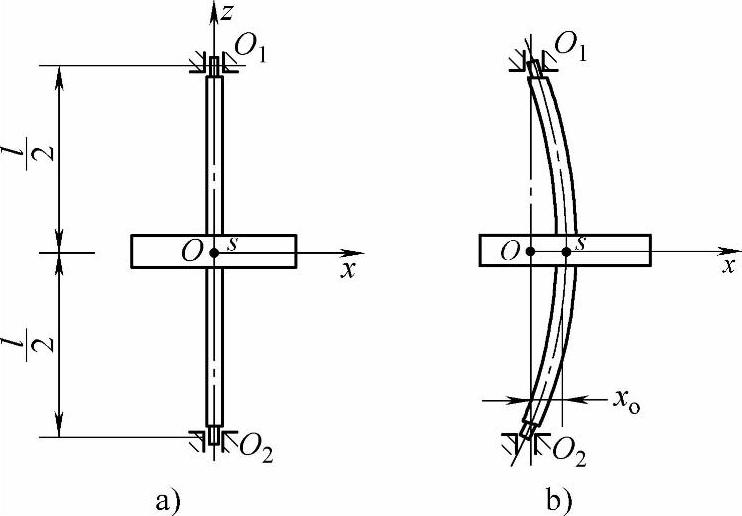
图7-1 对称单圆盘转子
a)原始状态 b)受扰动后产生的自由振动
令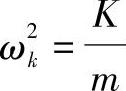
则有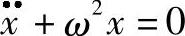
此方程的解为
x=Acos(ωkt+φ) (7-1)
式中A为振幅,由初始扰动而定;ωk为自由振动圆频率(1/s);t为振动时间;φ为初相位,由初始扰动而定。
这是一种周期性的简谐振动,其振动周期T为
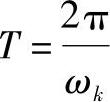
振动频率f为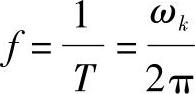
振动相位主要在两个或多个同频率的变化量进行时间先后的比较时有意义。式(7-1)表示了圆盘在振动中位移随时间的变化规律,如将位移对时间t求一阶、二阶导数,就分别得到振动的速度和加速度:
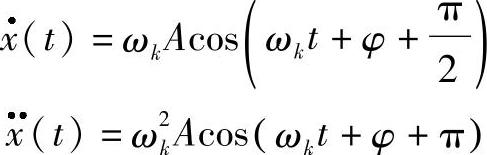
可见,简谐振动时的速度与加速度也是同频率的简谐振动,但其相位则分别比位移超前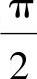 及π。
及π。
从上面所得的自由振动规律中可以看到,振幅和初相位可以随着初始条件的变化而变化,但自由振动的频率与初始条件无关。不管系统受到怎样的初始扰动,不管振动的振幅大小,自由振动的频率不变,只与系统本身的质量和刚度有关,或者说只取决于系统本身的结构参数,是系统本身的固有振动特性,因此称为固有频率。对转子而言即为临界转速。
(2)无阻尼受迫振动 转子在周期性变化的外力(干扰力)的作用下,所发生的振动称为受迫振动。形成干扰力的原因有很多,这里只讨论一种特定的情况,即转子在不平衡离心力作用下的强迫振动。
设前面讨论的转子,其重心G偏离转动轴线,与几何中心s点不重合,偏心距为e,见图7-2。当转子以角速度ω转动时,在转子上就产生了不平衡离心力meω2,这就是作用于转子上的干扰力。此力迫使轴产生弯曲,使s点或者说使整个转子围绕其平衡位置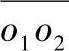 运动,这种运动称为涡动,也称弓状回转。这种运动与一根不转动的轴做横向弯曲振动是两种不同的物理现象。横向弯曲振动在轴内产生交变应力;弓状回转时轴内不产生交变应力。但是,使转子产生振动,以及对轴承产生交变作用力,从而造成机组的振动,两者都是一样的,因此对这两种运动形态,工程上常常不加区别。
运动,这种运动称为涡动,也称弓状回转。这种运动与一根不转动的轴做横向弯曲振动是两种不同的物理现象。横向弯曲振动在轴内产生交变应力;弓状回转时轴内不产生交变应力。但是,使转子产生振动,以及对轴承产生交变作用力,从而造成机组的振动,两者都是一样的,因此对这两种运动形态,工程上常常不加区别。
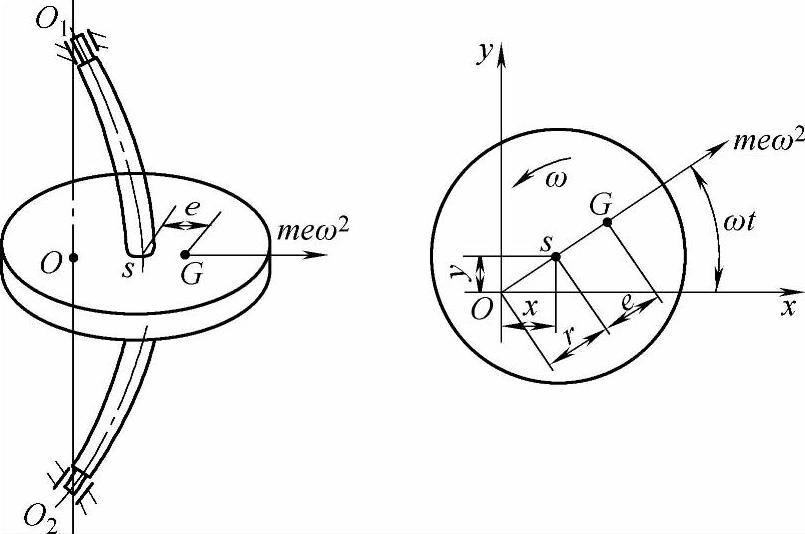
图7-2 单圆盘转子
以o点为原点,在圆盘平面上建立直角坐标系x-y。离心力随转子以角速度ω旋转,设在瞬时t,它在坐标轴x、y方向的分量分别为
Fx=meω2cosωt
Fy=meω2sinωt
显然,Fx、Fy必迫使转子在x、y方向做周期性运动。
在振动过程中,惯性力、弹性力和不平衡离心力三者相平衡。在x方向为

这就是s点在x方向上的运动微分方程式,是一个二阶线性非齐次微分方程。它的解可以写成如下形式:
x=C1cosωt+C2sinωt+Acosωt (7-3)其中,前两项是对应的齐次方程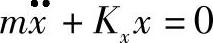 的解,即方程通解,相当于无外力作用时自由振动的解(即由初始扰动造成的);最后一项是方程的特解,由不平衡离心力引起的。由于实际转子总有阻尼存在,因此前两项会很快消失,最后只剩下最后一项特解部分。下面着重讨论特解部分,探讨由不平衡离心力引起的转子涡动规律。
的解,即方程通解,相当于无外力作用时自由振动的解(即由初始扰动造成的);最后一项是方程的特解,由不平衡离心力引起的。由于实际转子总有阻尼存在,因此前两项会很快消失,最后只剩下最后一项特解部分。下面着重讨论特解部分,探讨由不平衡离心力引起的转子涡动规律。
将x=Acosωt形式的特解代入式(7-2),得
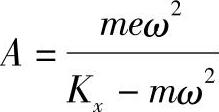
因而
可见在Fx作用下,s点将在x方向上作简谐振动,它的频率与Fx的频率是相同的。就是说转子在不平衡离心力这一激振力的作用下,发生同频率的振动,振幅与激振力大小、转子的质量、刚度及转速等有关。(https://www.chuimin.cn)
同理,在Fy作用下,在y方向的运动微分方程为

其特解为

如果转子及轴承在各个方面上的刚度是相同的,因而Kx=Ky=K,那么s点在x、y两个方向的运动规律可表示为

显然s点的涡动轨迹为一个圆,圆心在坐标原点o,半径为

对于实际转子,由于轴承刚度的各向异性,即Kx≠Ky,因此涡动轨迹为一椭圆,正像在用示波器观察转子涡动轴心轨迹时所看到的那样。
可见,实际上转子的运动状态是由两种运动合成:一种是转子绕其本身轴线的运动,设角速度为ω,称为自转;另一种是整个转子轴线绕其平衡位置的转动,称为涡动,或称为公转,设其涡动角速度为Ω。当ω=Ω,且方向一致,称为同步正运动,是工程上最常见的一种;如果ω=Ω,但方向相反,称为同步反运动,在风机的实际运行中也有发生。当ω≠Ω,且方向一致,称为异步正运动;反向时,称为异步反运动。
(3)阻尼对不平衡振动的影响
1)阻尼。通常在转子运动时,存在着各种各样阻尼运动的阻力,称为阻尼。阻尼能对转子振动起衰减和抑制作用。常见的阻尼有以下几种:①转子运动时与周围介质之间的摩擦阻尼。这种阻尼力的大小,在比较微小的振动时,与振动速度成正比,即阻尼力可表示为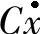 ,通常C为常数,这类阻尼称为线性阻尼。②滑动轴承中的油膜阻尼。③材料的内阻尼。④转子各零部件连接处、配合处可能形成的内摩擦阻尼。
,通常C为常数,这类阻尼称为线性阻尼。②滑动轴承中的油膜阻尼。③材料的内阻尼。④转子各零部件连接处、配合处可能形成的内摩擦阻尼。
上述各种阻尼中,对转子振动影响最大,因而也是对转子稳定运转影响最大的是轴承油膜阻尼。
2)阻尼系数。阻尼一般很复杂,这给研究转子运动带来困难。但在振动速度较小,阻尼作用较小时,工程上可用能量相当的办法,把各种阻尼简化成相当的线性阻尼,即把阻尼力仍表达为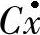 ,C为常数,称为线性阻尼系数。
,C为常数,称为线性阻尼系数。
由于阻尼作用的大小,不仅与阻尼系数大小有关,而且与系统其他参数的相对关系有关,因此工程上通常引用相对阻尼系数:

式(7-8)的分母是所谓临界阻尼系数。相对阻尼系数也称阻尼比,是一个量纲一的参数。
3)阻尼对转子不平衡振动的影响。在有阻尼的情况下,单圆盘转子的不平衡振动,可以抽象为见图7-3的单圆盘转子振动力学模型。此时的运动微分方程式为
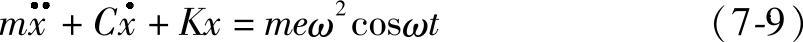
引用阻尼比ζ,则式(7-9)可改写为
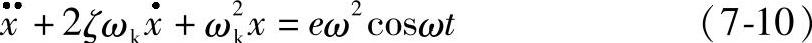
方程解的通解部分,就是运动初始时由于扰动引起的自由振动。它将由于阻尼的存在而很快消失,因此这里只研究特解部分,即稳态的不平衡强迫振动。
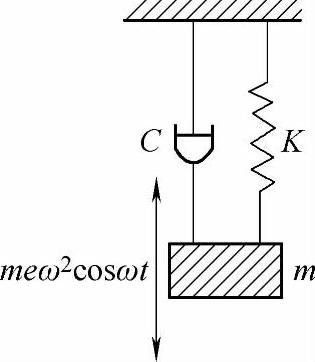
图7-3 单圆盘转子振动力学模型
设特解形式为x=Acos(ωt-φ),代入方程,可求出A值和φ值如下:
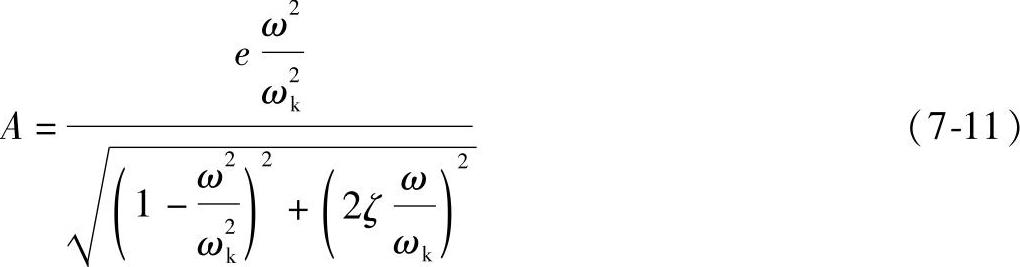
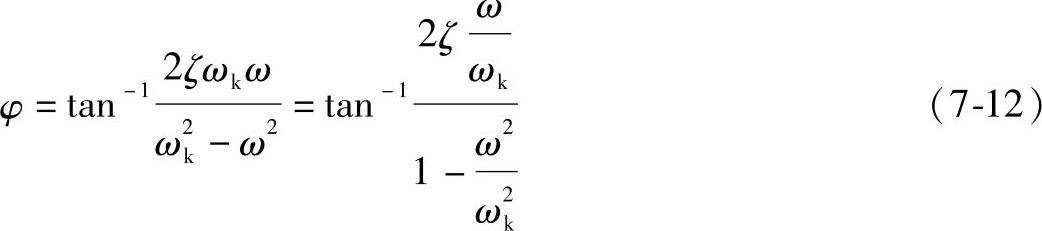
式中,A为振幅;φ为初相位角;ωk为转子无阻尼时的固有圆频率。
可见,振幅及相位都与转速及阻尼比有关,在不同的阻尼比下,可以画出不同的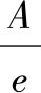
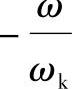 曲线及
曲线及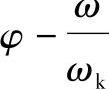 曲线。前者称为振动的振幅-频率特性曲线,简称幅频曲线,见图7-4。后者称为振动的相位-频率特性曲线,简称相频曲线,见图7-5。
曲线。前者称为振动的振幅-频率特性曲线,简称幅频曲线,见图7-4。后者称为振动的相位-频率特性曲线,简称相频曲线,见图7-5。
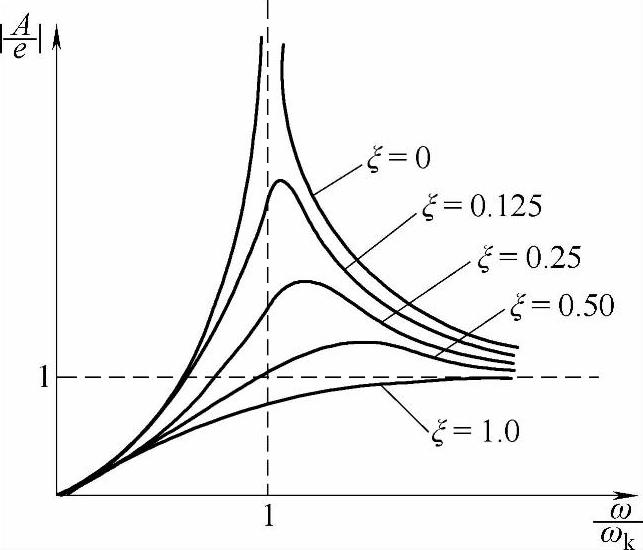
图7-4 振幅-频率特性曲线
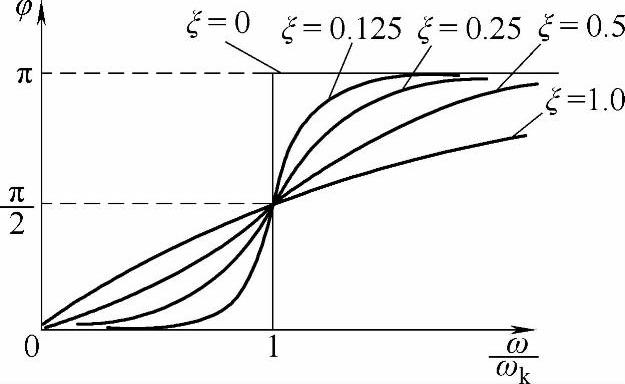
图7-5 相位-频率特性曲线
相关文章

当SEq<0时,特征值p1、p2为两个实数,其中一个为正实数,所以电力系统受扰动后,功角偏差Δδ最终以指数曲线的形式随时间不断增大,因此系统是不稳定的。这种丧失稳定的形式称为非周期性地失去同步。称为实用判据,常被应用于简单电力系统和一些定性分析的实用计算中。在稳定工作范围内,自由振荡的频率为图14-2fe、SEq随δ的变化这个频率通常又称为固有振荡频率。......
2025-09-29

由于振动诊断具有诊断结果准确可靠和便于实时诊断等诸多优点,因而它成为应用最广泛、最普遍的诊断技术之一。特别是近年来,随着振动信号采集、传输以及分析用仪器技术性能的提高,更进一步地促进了振动诊断技术在机械故障诊断中的应用。ψ称为简谐振动的相位,是时间t的函数,单位为rad。表5.2根据振动后果选择振动监测参数测量参数选择的另一个问题是振动信号统计特征量的选用。......
2025-09-29

沟通交流最常见、最主要的形式是语言和言语,因此本书主要根据中国大陆对沟通障碍的分类形式,分别介绍语言障碍和言语障碍的类型。构音障碍的常见类型有以下四种。常见的语流障碍包括口吃和速语症两种。速语症的主要特征为:①语速过快;②发音短促;③语音错误;④音节遗漏。存在重度语言障碍的儿童常常在沟通中出现问题,且存在口头语言障碍的儿童可能在阅读和书写上都存在困难。......
2025-09-29

滚动轴承振动按产生机理可分为以下三种类型:轴承结构的固有振动1)把外圈看作是弹性体引起的固有振动,如表5-1所示。表5-1 套圈弹性固有振动类型表5-2 套圈刚体固有振动类型表5-3 滚动体固有振动强迫振动1)滚动体通过振动 当轴承运转时滚动体周期通过载荷作用线引起的振动,如表5-4所示。表5-6 滚道表面缺陷引起的轴承振动频率滚动轴承的振动往往是以上各类振动共同作用的结果。......
2025-09-29

肺活量是身体发育是否健康的一个指标。探究活动活动一使用简易肺活量测量袋测量,你的肺活量有多少?活动二比较班内同学的肺活量,锻炼对肺活量有什么影响?中长跑运动员和游泳运动员的肺活量可达6000毫升。( )3.肺活量是指人体吸入最多空气后,呼出气体的量。......
2025-09-29

电压过大地偏离额定值将对用户产生不良的影响。电压偏高时,照明设备的寿命将要缩短。电压偏移过大,除了影响用户的正常工作外,对电力系统本身也有不利影响。目前,我国规定的在正常运行情况下供电电压的允许偏移如下:35kV及以上供电电压正、负偏移的绝对值之和不超过额定电压的10%;10kV及以下三相供电电压允许偏移为额定电压的±7%;220V单相供电电压允许的偏移为额定电压的+7%和-10%。......
2025-09-29

2)通带内增加了波动,在ωc-2π/N处出现过冲为0.089的最大正峰。3)阻带内产生了余振,在ωc+2π/N处出现过冲为-0.090的最大负峰。图3-2是当N分别取4、8、16、32时Hdg(ω)和Hg(ω)的波纹变化。图3-3中,当阶数N由24增大到216时,由于旁瓣数量的增加致主瓣能量占比逐渐降低,最大正峰的过冲程度也随着N的增大而逐渐减小,但阶数增大至210以后,过冲程度基本没有再改善。......
2025-09-29

转子发动机是由德国的菲力斯·汪克尔与NSU公司共同开发,也称为汪克尔发动机。转子内的机油量始终保持一定的量,否则会发生振动,因此内置有为排出过剩机油的泵型圆盘。配备两个转子的转子发动机主轴每旋转1周进行两次做功,与4气缸四冲程循环往复式发动机相同。目前,汪克尔发动机研发了2个转子配置6个进气端口的6端口进气系统。......
2025-09-29
相关推荐