流体在空间的流动可以说都是三元流动，运动参数是空间三个坐标的函数。因此对于工程技术中的问题，在保证一定精度的条件下，尽可能将三元流动简化为二元流动，甚至一元流动来求近似解。流场的运动参数只是两个坐标的函数时称为二元流动。若实际流体的粘性很小，可以忽略，以管横截面上的平均流速来描述管内流动，即将二元流动化为一元流动求解。图2-3 圆管内流动a）二元流动 b）一元流动......
2023-08-20
风机压力损失修正法-建筑及空调风机的工程设计、使用与维修
【摘要】：表6-14 管道内表面的平均绝对粗糙度当管道内表面的平均绝对粗糙度不同时，仍可利用图6-13和表6-12、表6-13，但对所查得的单位长度摩擦损失值要进行修正，即应乘以管道粗糙度的修正系数ε值：pm′=εpm 式中，pm′为实际使用条件下的单位长度摩擦损失；pm为从线算图和计算表中查得的单位长度摩擦损失值。图6-14 管道粗糙度的修正系数a）粗糙管K=3.0mm b）中等粗糙管K=0.9mm c）中等光滑管K=0.09mm d）光滑管K=0.03mm图6-15 海拔和温度对摩擦损失的修正系数
图6-13、表6-12和表6-13均是按钢板制管道，管道内表面的绝对粗糙度K=0.15mm和标准状态空气，在标准大气压的条件下编制的。当条件改变时，仍可用上述图表，但对查出的值要进行修正。
（1）绝对粗糙度的修正 管道可用各种材料制作，如钢板、铝板、塑料板、玻璃钢，混凝土和砖等。各种管道内表面的绝对粗糙度均不相同，有的相差很大。表6-14列出了部分管道内表面的平均绝对粗糙度。
表6-14 管道内表面的平均绝对粗糙度
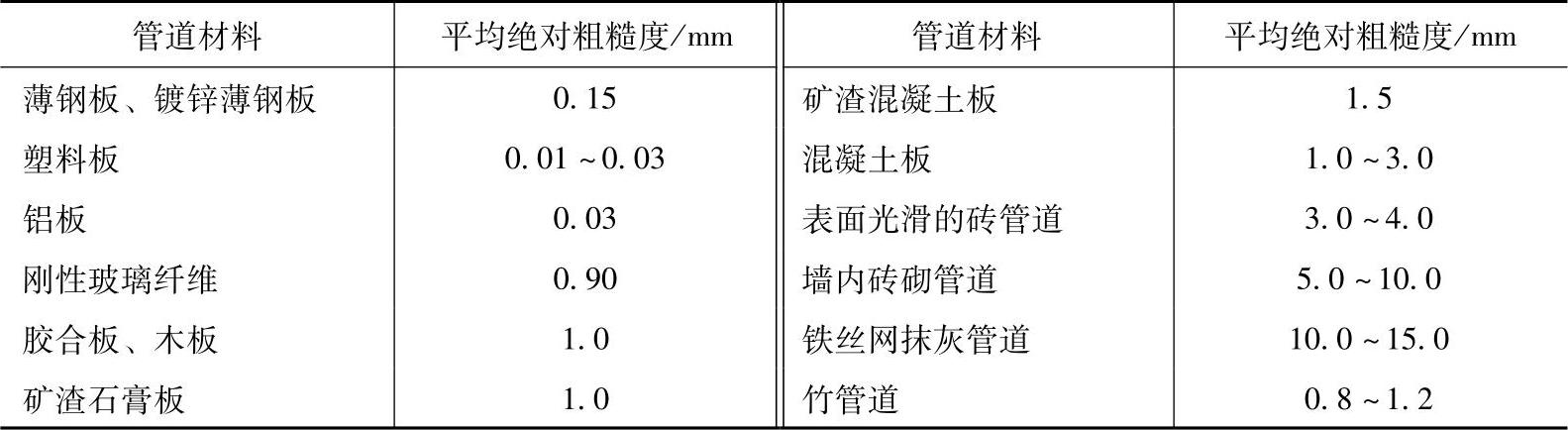
当管道内表面的平均绝对粗糙度不同时，仍可利用图6-13和表6-12、表6-13，但对所查得的单位长度摩擦损失值要进行修正，即应乘以管道粗糙度的修正系数ε值：
pm′=εpm （6-17）
式中，pm′为实际使用条件下的单位长度摩擦损失（Pa/m）；pm为从线算图和计算表中查得的单位长度摩擦损失值（Pa/m）。
ε值可从图6-14查到。图6-14a为粗糙管道，K=3.0mm；图6-14b为中等粗糙管道，K=0.9mm；图6-14c为中等光滑管道，K=0.09mm；图6-14d为光滑管道，K=0.03mm。
（2）海拔和温度的修正系数 从管道的摩擦损失计算式中可以看出，管道的单位长度摩擦损失pm与空气的密度及运动粘度有关。空气的密度是温度的函数，同时也受海拔的影响。而运动粘度又取决于温度和大气压力（海拔）。图6-15给出随温度和海拔变化的修正系数εt和εh。
所以，使用条件下管道的实际单位长度摩擦损失可按式（6-18）计算：
pm′=εtεhpm （6-18）
修正系数分别按式（6-19）、式（6-20）计算：
式中，t′为管道中空气的实际温度（℃）；p′为实际的大气压力（kPa）。
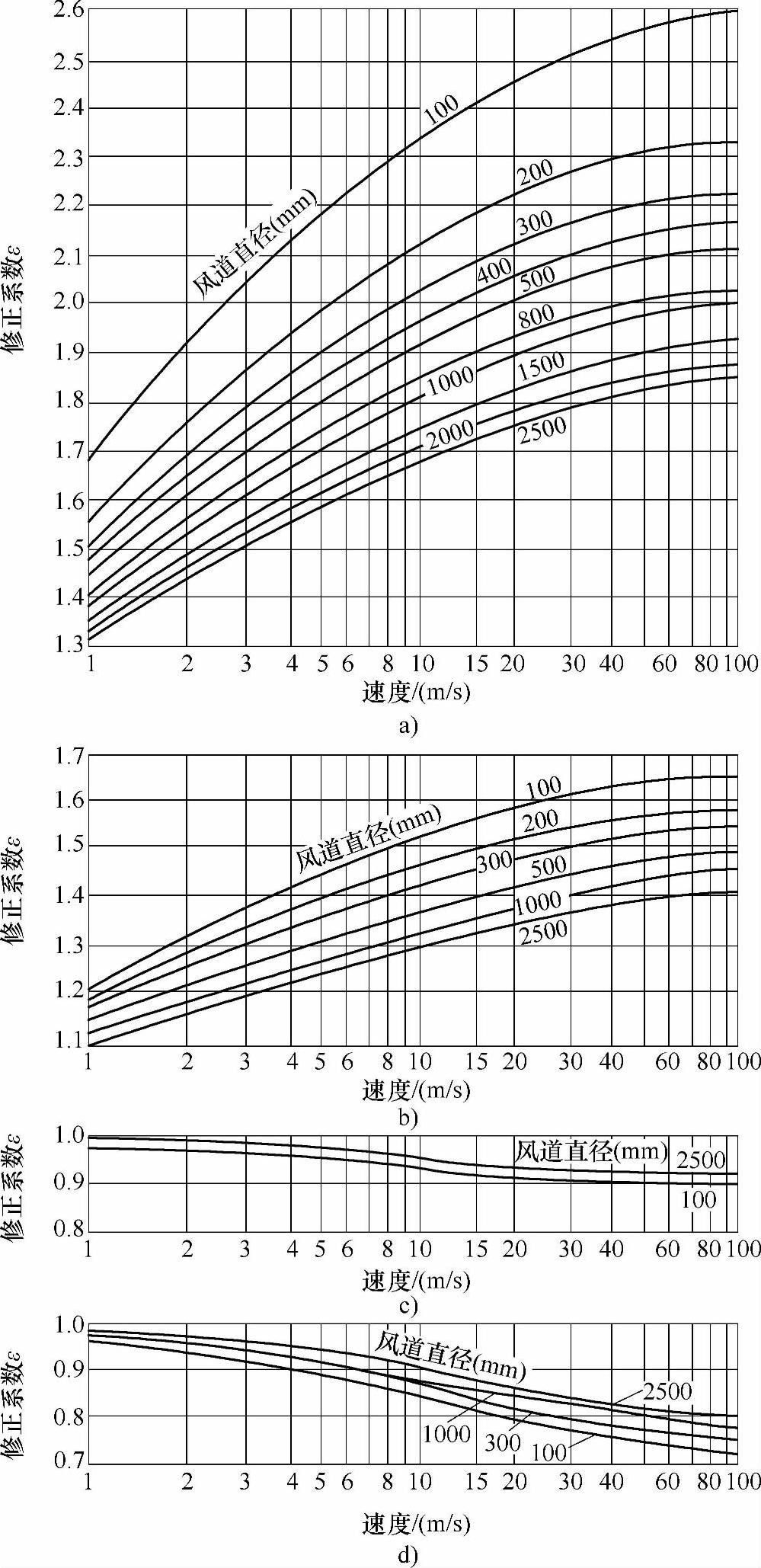
图6-14 管道粗糙度的修正系数
a）粗糙管K=3.0mm b）中等粗糙管K=0.9mm c）中等光滑管K=0.09mm d）光滑管K=0.03mm
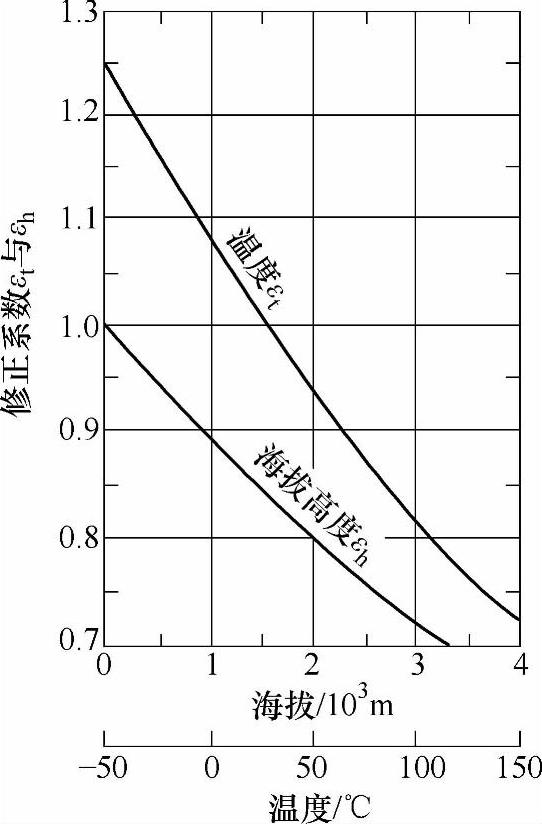
图6-15 海拔和温度对摩擦损失的修正系数
有关建筑及空调风机的工程设计、使用与维修的文章
- 详细阅读
-
建筑与空调风机工程设计维修详细阅读
能量方程式是建立流体通过旋转叶轮时，获得能量的定量关系式。此方程式是欧拉在1756年首先推导出来的，所以又称欧拉方程。能量方程的表达式 已知原动机传给风机轴的功率P为P=Mω式中，M为通风机叶轮轴的力矩（N·m）；ω为通风机叶轮的旋转角速度（1/s）。pT∞=ρ 式即为能量方程的表达式。能量方程式的修正 实际情况下，叶轮叶片数有限，流体具有粘性，因而实际应用时，应对式进行修正。......
2023-08-20
-
通风机管网及其特性-建筑及空调风机的工程设计详细阅读
根据工作情况的不同，有的通风机只有进口管网，有的通风机只有出口管网。如果把工作场所当作管网的一部分，一并计算其静阻力，则式（6-2）中Δpg一项不存在，于是该式所表示的管网特性即为狭义的管网特性。K值表征了管网的特性，称为“管网特性系数”。今后除特殊指明外，提到的管网及管网特性都是指狭义的管网及管网特性。有了R与qV的对应关系，就可按照上述过程求出管网特性系数K，并绘出管网特性曲线。......
2023-08-20
-
建筑及空调风机的设计、使用与维修详细阅读
根据增压值的大小，离心风机可分为以下三类：①低压风机。混流风机的性能介于离心式与轴流式之间。按照动叶片的调节方式，混流风机可分为动叶不可调节、动叶半调节及动叶全调节等三种型式。回转式风机主要有罗茨鼓风机及压缩机等类型。图4-3所示为罗茨鼓风机。目前定型生产的各种类型风机的使用范围是相当广泛的。其中叶片风机中的离心种类的风机，工作区间最广，产品种类、型号、规格也最多。......
2023-08-20
-
建筑及空调风机工程设计、使用与维修的相似条件详细阅读
几何相似 这是指模型与实物的几何形状相同，对应的线性长度比为一定值，对应角度相等。几何相似是运动相似的先决条件。根据气体流动的气动热力过程及能量传递过程的相似要求，两个通风机的气流过程相似条件可归结如下：几何相似、叶片进口的速度三角形相似、雷诺数相等。下面将证明只要满足上述相似条件，两个通风机一定是相似的。......
2023-08-20
-
通风机量纲一的参数：建筑及空调风机工程设计、详细阅读
压力系数，由于两个通风机相似，对应点的速度三角形相似，欧拉数相等。设1、2分别为通风机的进、出口截面，由欧拉数相等可得经变换后得因运动相似，则又因式中，Δp、ΔpM为实物和模型进、出截面的静压差。对于轴流通风机，同样有，，分别与模型的、相等的关系。因此可以说通风机的量纲一的参数、、分别是衡量各种不同类型通风机的压力p、流量qV及功率P大小的特征值。......
2023-08-20
-
建筑空调风机工程设计与维修的声强级详细阅读
某一点的声强，是指该点在单位时间内通过垂直于声传播方向的单位面积上声波的能量。正常人耳引起听觉的声强为10-12W/m2，引起人耳听觉疼痛的声强是10W/m2。从痛阈到听阈，声强比值达1013倍，数值过大，极不方便。况且声音的强弱只有相对意义，所以声强绝对值实际上是不怎么经常用的。为了方便起见，选用正常人耳的听阈声强值作为基准声强，并用对数表示，则LI为：式中，LI为声强级；I0为基准声强，I0=10-12W/m2，这样基准声强下的听阈声就是零分贝。......
2023-08-20
-
建筑与空调风机工程设计：能量损失计算详细阅读
沿程损失的计算 气体在横断面不变的管道内流动时，沿程损失hf可按式计算：沿程压力损失Δpm为式中，Δpm为管道的沿程压力损失；λ为沿程（摩擦）阻力系数；c为管道内气体的平均流速（m/s）；ρ为气体的密度；l为管道的长度；d为管道的直径。沿程压力损失也可表示为而单位长度的沿程损失，通常称为比摩阻，用符号pm表示。对于长、宽分别为a和b的矩形管道为沿程阻力系数可按式计算：......
2023-08-20
相关推荐