首页理论教育混合气体的工程设计和维修

混合气体的工程设计和维修

2023-08-20 理论教育版权反馈

【摘要】：分压力定律和分容积定律处于平衡状态下的理想气体混合物，内部各处温度均匀一致，因而每一组元的温度都相等，都等于混合气体的温度。混合气体中某组元的量与混合气体总量之比，称为混合气体中该组元的含量。由于采用不同的物量单位，混合气体各组元的含量有不同的表示方法。故混合气体的比热容为即混合气体的比热容，等于各组元气体的比热容与其质量分数的乘积之和。

通风机输送的气体往往不是单一成分，而是由多种气体组成的混合物，如空气，还有烟气等。组成混合气体的各单一气体称为混合气体的组元，当各组元均为理想气体时，由它们所组成的混合气体也必定是理想气体，因此，前述理想气体热力性质的分析，均适用于理想气体的混合物。

（1）分压力定律和分容积定律处于平衡状态下的理想气体混合物，内部各处温度均匀一致，因而每一组元的温度都相等，都等于混合气体的温度。同样，由于处于平衡状态，每一组元的分子都均匀地分布在混合物的容器中，即各组元所占的容积都相等，都等于混合物的容积。

1）分压力和道尔顿分压力定律。在容器中，每一组元的分子都会对容器壁撞击而产生一定的压力，各组元在理想气体混合物的温度下单独占据混合物所占据的容积V时，产生的压力称为该组元的分压力，用p_i表示，见图1-7。

各组元气体分子的热运动不应该存在其他组元分子而受到影响，应与各组元单独占据混合物所占体积的热运动一样。理想气体混合物的压力是各组元分子撞击器壁而产生的。实验证明，理想气体混合物的压力p，等于各组元的分压力p_i之和，称为道尔顿分压力定律。即

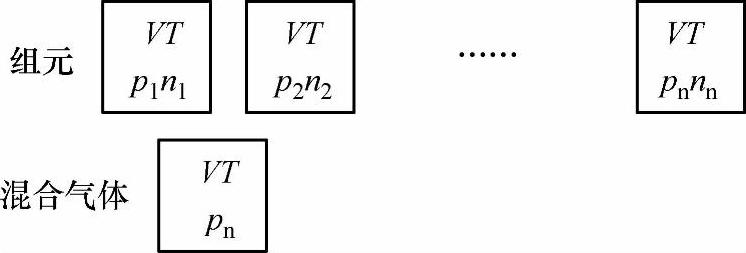
图1-7 分压力

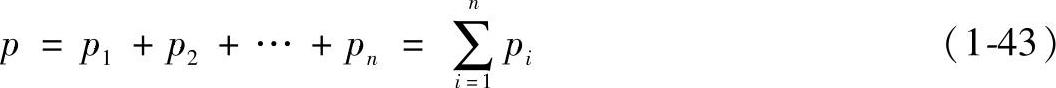
2）分体积和分体积定律。所谓分体积，是指各组元处于混合物的温度和压力下，单独存在时所占据的体积，用V_i表示，如图1-8所示。

实验证明，理想气体混合物的体积V，等于各组元的分体积V_i之和，称为亚美格分体积定律。即

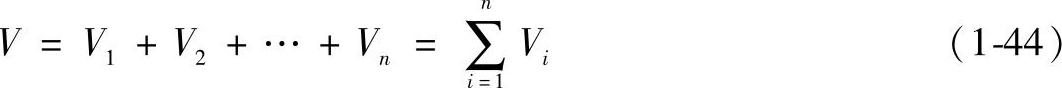
实际上，理想气体混合物中各组元都充满了整个体积，所谓分体积，只是假想将各组元在混合气体的温度和压力下，分别集中于各自所占据的体积内，以便于用体积来表示各组元气体数量的多少。

（2）理想气体混合物的成分理想气体混合物的性质取决于各组元的性质和数量。混合气体中某组元的量与混合气体总量之比，称为混合气体中该组元的含量。由于采用不同的物量单位，混合气体各组元的含量有不同的表示方法。

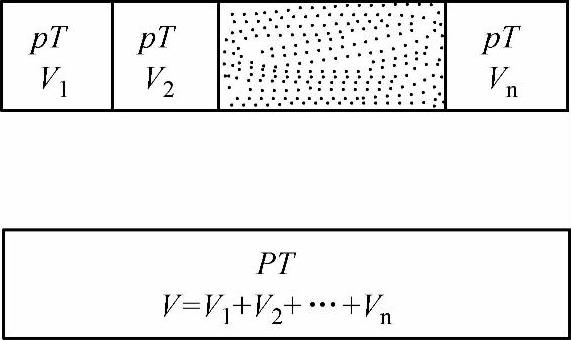
图1-8 分体积

1）质量分数w_i。在理想气体混合物中，各组元的质量m_i与混合物总质量m之比，称为该组元的质量分数，符号为w_i，即

因为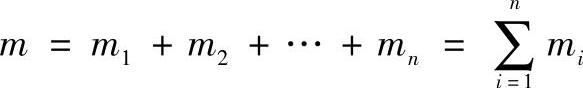

因此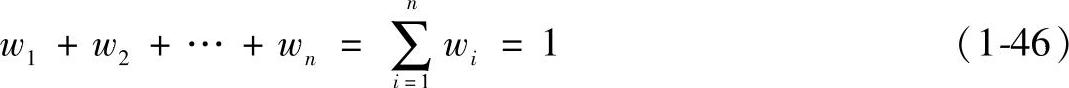

2）体积分数φ_i。理想气体混合物中，某组元的体积V_i与混合物总体积V之比，称为该组元的体积分数。记为φ_i。即

根据分体积定律，有

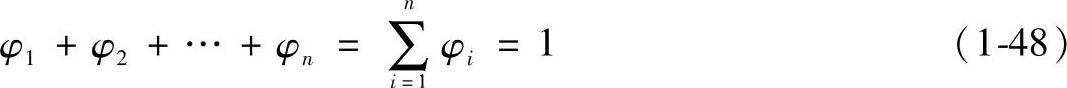
3）摩尔分数x_i

理想气体混合物中，某组元的物质的量n_i与混合物总物质量n之比，称为该组元的摩尔分数。符号为x_i，即

因为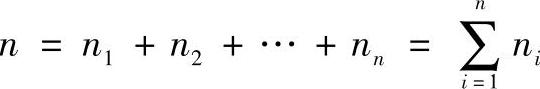所以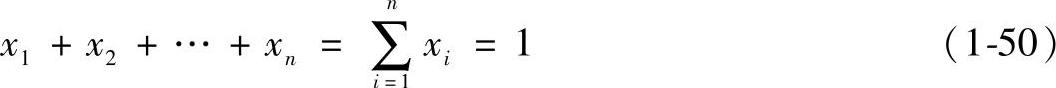

经证明，各含量之间的换算关系如下：

体积分数与摩尔分数在数值上相等。即

φ_i=x_i （1-51）

质量分数与体积分数（或摩尔分数）的换算关系为

式中，M_i、M为某组元气体、混合气体的摩尔质量。

（3）折合摩尔质量与折合气体常数气体常数取决于气体的摩尔质量。为了便于计算，取混合物的总质量m与混合物的总物质的量n之比为混合物的摩尔质量，称为折合摩尔质量或平均摩尔质量。即

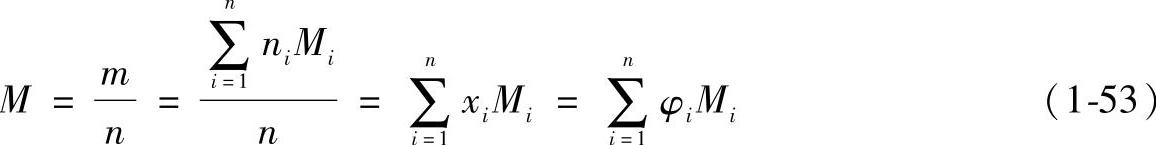
即混合气体的折合摩尔质量等于各组元的摩尔质量与它们的体积分数（或摩尔分数）乘积的总合。

求出理想气体混合物的折合千摩尔质量后，即可求出混合气体的折合气体常数R[J/（kg·K）]为

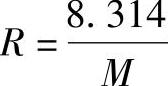
（4）混合气体的比热容确定混合气体比热容的依据是能量守恒定律，即在加热过程中，一定数量的混合气体温度升高1℃所需要的热量，应等于各组元气体温度升高1℃所需热量的总合。故混合气体的比热容为

即混合气体的比热容，等于各组元气体的比热容与其质量分数的乘积之和。同样，混合气体的摩尔热容和摩尔定容热容分别为