流体发电已经被报道用于能量转换以及流体流速和溶液浓度的检测。通常，有两种类型的流体通道能够用于流体发电。图4.57MFG中微流控芯片的制造和表征［7］采用软光刻技术制造微流控芯片；具有设计结构的Si模具照片；图案化PDMS复制品的图像；PDMS复制品上的微柱阵列的SEM图像，插图为高放大倍数下，视角为30°时PDMS结构的图像；透明微流控芯片的图像Peng等制备出一种纤维状流体纳米发电机。图4.59纳米管中的流动发电过程......
2023-06-30
雷诺数Re及其在流体运动中的应用
【摘要】：根据量纲理论，上述诸参数可以组成一个量纲一的量：式中，ν为流体的运动粘滞系数，此量纲为1的量称为雷诺数。对应以上两个临界流速的雷诺数分别如下：下临界雷诺数上临界雷诺数实际上水流总是受到各种因素的扰动，过渡状态的层流极不稳定，一受扰动，很容易变成紊流；而扰动又是经常发生的，因而下临界雷诺数具有判别流态的实用价值。
层流和紊流这两种流动状态的形成，与流体的粘性系数μ、密度ρ、管道的特征尺寸为直径d，以及特征速度为管内的平均流速c等有关。根据量纲理论，上述诸参数可以组成一个量纲一的量：
式中，ν为流体的运动粘滞系数（m2/s），
此量纲为1的量称为雷诺数。从雷诺实验可知，当流体做层流流动时，在μ、ρ和d不变的情况下，流速减少，意味着Re数减少，此时粘性力起着重要的作用。当流体做紊流流动时，流速的增大意味着Re数的增大，此时粘性力起的作用就相对地较小。流体流动从层流转变成紊流，可以理解为流体的运动丧失了稳定性。当流体流动受到外界扰动时，在某种情况下这种扰动会因流体内部粘性力对运动的阻尼作用而衰减，在另一种情况下则会继续扩展而使流动丧失其稳定性。因此，流动状态的变化取决于扰动和粘性力的抗衡程度，而Re数则是判别流动型态的准则数。
将流态转变时的流速称为临界流速，由层流向紊流转变和由紊流向层流转变时的临界流速是不同的，前者较大，称上临界流速，以c′cr表示；后者较小，称下临界流速，以ccr表示。
对应以上两个临界流速的雷诺数分别如下：
下临界雷诺数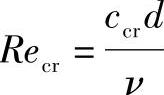
上临界雷诺数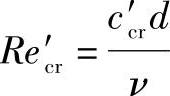
实际上水流总是受到各种因素的扰动，过渡状态的层流极不稳定，一受扰动，很容易变成紊流；而扰动又是经常发生的，因而下临界雷诺数（简称临界雷诺数）具有判别流态的实用价值。
实验证明，对于圆管，Recr=2300。当Re≤2300时，流动是层流；Re＞2300时，流动是紊流。
在通风机中，由于气流速度较大，大多数都是紊流状态。
有关建筑及空调风机的工程设计、使用与维修的文章
- 详细阅读
-
流体网格法及其在解决激波问题中的应用详细阅读
因此在用流体网格法求解流体动力学方程时，必须考虑对激波的处理，即解决间断的问题。本节在介绍流体网格法以及说明流体网格法差分过程中均提到了差分中的人工粘性系数q，这种加入人工粘性系数的方法目前在跨音速流动的数值计算中是非常有效的。......
2023-07-02
-
水在岩土体中的存在形式及其在工程中的应用详细阅读
因此，在潜水面以上常形成毛细水带。图1-3各种形态的水在岩层中的分布气态水、结合水、毛细水和重力水在地壳最表层岩土中的分布有一定的规律性。当在松散岩土中开始挖井时，岩土是干燥的，但是实际上存在着气态水和结合水；继续向下挖，发现岩土潮湿，说明岩土中有毛细水存在；再向下掘进，便开始有水渗入井中，并逐渐形成地下水面，这就是重力水。......
2023-09-23
-
权威效应及其在领导中的应用详细阅读
因此，这两种心理就诞生了权威效应。在人际交往中，利用“权威效应”，还能够达到引导或改变对方的态度和行为的目的。因此，一个优秀的领导肯定是企业的权威，或者为企业培养了一个权威，然后利用权威暗示效应进行领导。......
2023-12-01
-
肽类激素在体育运动中的应用详细阅读
目前，国际奥委会禁用的此类激素包括人绒毛膜促性腺激素、促性腺激素（如LH）、促肾上腺皮质激素、人生长激素、胰岛素样生长因子以及上述各物质的所有释放因子和它们的类似物、促红细胞生成素、胰岛素等。正常男子和非妊娠妇女的垂体也可以生成和分泌hCG，但是其数量极微。在临床上，EPO主要用来治疗慢性肾衰竭所造成的贫血以及其他类型的贫血患者。......
2023-10-19
-
浮力原理及其在水饺烹煮中的应用详细阅读
图2-27 物体沉浮条件2.7.3 浮力原理的定义物体依据其本身在液体或气体中沉浸或飘浮的状况，可以分成沉体与浮体两种状态，所以浮力原理可分成沉体所受到的浮力与浮体所受到的浮力两个部分来表示。飘浮在流体的物体，称为浮体，受到的浮力等于物体排开流体的重力或浮体本身的重力。试用浮力原理说明在日常生活水饺的烹煮过程中，水饺刚放入水中时会下沉，而在水饺煮熟时会上浮的原因。......
2023-06-29
-
变位齿轮简介及其在传动中的应用详细阅读
为了使两个固定齿轮装在同一轴上，且能分别与齿轮1正常啮合，可采用变位齿轮。若采用变位齿轮则可使小齿轮齿根厚度增大，从而使两轮的抗弯能力相近。负变位齿轮分度圆上的齿厚及齿根圆上的齿厚都减小，齿顶变宽。2）变位齿轮的一些几何尺寸发生了变化。1）高度变位齿轮传动。两齿轮变位系数之和不等于零，即x1+x2≠0的一对齿轮传动称为角度变位齿轮传动。......
2023-06-25
-
在重力场中的运动规律详细阅读
重力场中的火箭运动存在重力损失mgsinθ和空气阻力损失D。因而在重力场中火箭的运动方程式为式中，m为火箭质量。式可以用与式和式相对应的无量纲式表示。式与无重力场式相比，可以看出仅增加了右边最后项。因此，当高度为h=100km时，把这些已知的数据代入式中，可以得出重力加速度为g≈9.48m/s2，这是地球海平面上的97%左右。即，从地面到100km高度的重力变化仅减小3%，因此在推进剂燃烧期间将重力加速度可以看成g常数也无妨。......
2023-06-28
相关推荐