首页理论教育叶轮内流体运动与速度三角形研究成果

叶轮内流体运动与速度三角形研究成果

2023-08-20 理论教育版权反馈

【摘要】：流体在叶轮中除作旋转运动外，同时还从叶轮进口向出口流动，因此流体在叶轮中的运动是一种复合运动。图1-4示出流体在叶轮内运动的圆周速度、相对速度和绝对速度。流体沿叶轮流道的运动，称相对运动，见图1-4b，其运动速度称相对速度，符号w表示，其方向为叶片的切线方向、大小与流量及流道形状有关。通常将叶片切线与圆周速度反方向之间的夹角，称为叶片安装角，用βa表示。求出u、vm及β后，即可按比例画出速度三角形。

流体在叶轮中除作旋转运动外，同时还从叶轮进口向出口流动，因此流体在叶轮中的运动是一种复合运动。图1-4示出流体在叶轮内运动的圆周速度、相对速度和绝对速度。

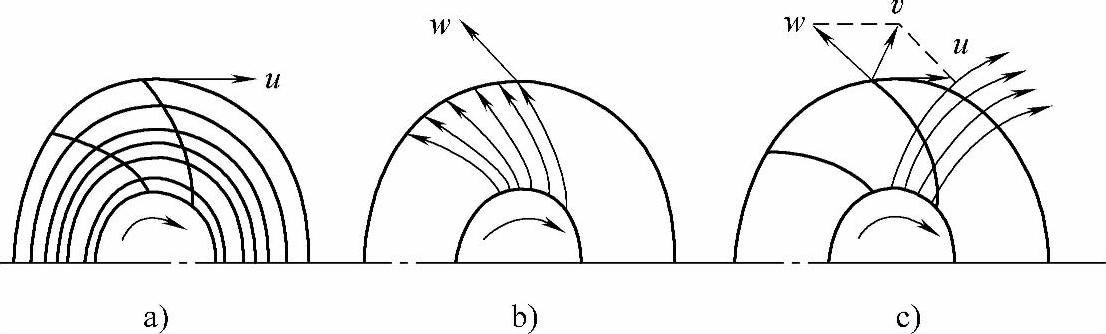
图1-4 流体在叶轮内运动的圆周速度、相对速度和绝对速度

a）圆周速度 b）相对速度 c）绝对速度

当叶轮带动流体作旋转运动时，流体具有圆周运动（牵连运动），见图1-4a。其运动速度称为圆周速度，用符号u表示，其方向与圆周切线方向一致，大小与所在半径及转速有关。

流体沿叶轮流道的运动，称相对运动，见图1-4b，其运动速度称相对速度，符号w表示，其方向为叶片的切线方向、大小与流量及流道形状有关。

流体相对静止机壳的运动，称绝对运动，见图1-4c，其运动速度称绝对速度，用符号v表示。它是以上两个速度的向量和，即

v=u+w （1-19）

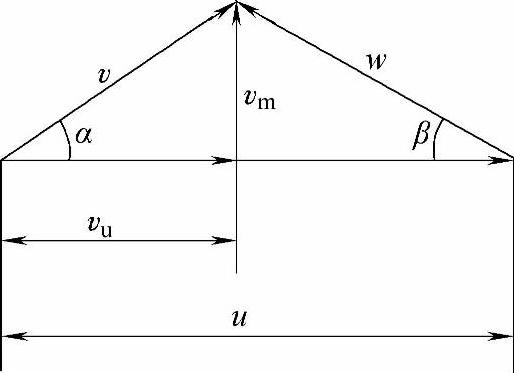
图1-5 速度三角形

由这三个速度矢量组成的矢量图，称为速度三角形，见图1-5。图中，v_u为绝对速度在圆周方向的分量，称为圆周分速度；v_m为绝对速度在轴向的分量，称为轴向速度；α是绝对速度与圆周速度之间的夹角，称为绝对速度角；β是相对速度与圆周速度反方向的夹角，称为流动角。

通常将叶片切线与圆周速度反方向之间的夹角，称为叶片安装角，用β_a表示。当流体沿叶片切线运动时，β=β_a。

叶轮叶片进、出口处的圆周分速度为

v_1u=v₁cosα₁v_2u=v₂cosα₂

叶轮进、出口的轴向速度为

v_1m=v₁sinα₁v_2m=v₂sinα₂

速度三角形一般只需已知三个条件就可画出。根据风机的设计参数，可以求出u、v_m和β角。

（1）求圆周速度u（m/s）

式中，D为叶轮直径（计算点的直径）（m）；n为叶轮转速（r/min）。

（2）求轴向速度v_m（m/s）

式中，q_VT为理论流量（m³/s）；q_V为实际流量（m³/s）；η_V为容积效率（%）；A为有效截面积（与轴向速度v_m垂直的面积）（m²）。

考虑到有效截面积被叶片厚度占去一部分，此时

式中，ψ为排挤系数；z为叶片数；σ为圆周方向的叶片长度；b为叶片宽度。

（3）求相对速度w的方向或β角当叶片无限多时，相对速度w的方向应与叶片表面相切，β与叶片安装角β_a相等。β_a在设计时是根据经验数值选取的。

求出u、v_m及β后，即可按比例画出速度三角形。