STAR-CCM+求解器主要有分离式求解器和耦合式求解器两种，如图2-102所示。分离式求解方法主要用于不可压缩或低马赫数压缩性流体的流动。耦合求解方法则可以用于高速可压缩流动。对于高中速可压缩流动，或需要考虑体积力的流动，求解问题时网格要比较密。如果采用耦合式求解方法求解能量和动量方程，可较快地得到收敛解。缺点是需要的内存比较大。目前，分离解法多用于不可压流计算，而耦合解法多用于可压流计算。......
2023-10-17
通风管道的流速求解及应用
【摘要】：连续方程式是在质量守恒定律的基础上建立起来的，可表述为：单位时间内流入控制体的气体质量与流出控制体的气体质量相等，且等于常数。连续性方程式普遍适用于任何工质的稳定而连续的流动。图1-1 通过流道的一维稳定流动式即为稳定流动的连续性方程式。式是不可压缩流体的连续性方程式。江面窄处水流速度大，江面宽处水流缓慢的现象，正是体现连续性方程的道理。解：对于通风管道，可采用不可压缩流体的连续性方程求解：A1c1=A2c2，则c2==
连续方程式是在质量守恒定律的基础上建立起来的，可表述为：单位时间内流入控制体的气体质量与流出控制体的气体质量相等，且等于常数。连续性方程式普遍适用于任何工质的稳定而连续的流动。
设有一任意流道（见图1-1），流道中截面1-1的截面积为A1（m2），气体流经此处时的比体积为v1（m3/kg），流速为c1（m/s）。则单位时间内流过1-1截面的质量，即质量流量qm1为
同理，流过2-2截面的质量流量为：
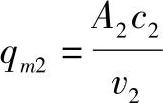
根据能量守恒定律，各截面的质量流量应相等，即
式中，qm为质量流量（kg/s）。
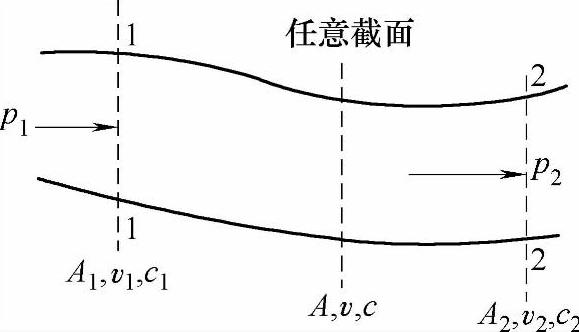
图1-1 通过流道的一维稳定流动
式（1-11）即为稳定流动的连续性方程式。它给出了流速、截面积与比体积之间的关系。这个关系式是计算管道截面积和流量的基本公式。
在通风机中，由于气体压力较小，压力变化也较小，气体在流动中可近似认为其密度不变，式（1-11）可简化为
qV=A1c1=A2c2=常数 （1-11a）
式中，qV为体积流量（m3/s）。
式（1-11a）是不可压缩流体的连续性方程式。它说明不可压缩流体在流动过程中，不仅质量流量保持不便，而且体积流量也保持不变，其流体的速度与横截面积成反比。江面窄处水流速度大，江面宽处水流缓慢的现象，正是体现连续性方程的道理。
【例题1】 已知某通风管道的进口直径为40cm，速度为20m/s，出气口的面积为40×24cm2。求出气口的速度。
解：对于通风管道，可采用不可压缩流体的连续性方程求解：A1c1=A2c2，则c2==
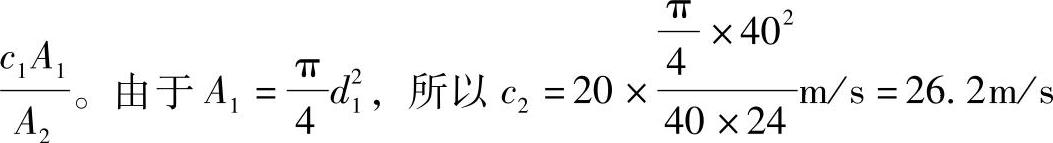
有关建筑及空调风机的工程设计、使用与维修的文章
- 详细阅读
-
整数的表示方法及补码求解步骤详细阅读
上面介绍的表示方法称为原码表示法。为统一加减运算规则，方便计算机运算，数值为负的整数在计算机内部实际上是采用补码来表示的。负整数补码求解的步骤为：先将负整数转换成原码的形式，最高位即符号位肯定为1，将除符号以外的每一位取反，得到称为反码的表示形式，最后将反码的最低位（末位）加1，即可得到补码的表示形式。......
2023-10-22
-
求解-SAMCEF有限元分析与应用实例详细阅读
单击Solver模块图标，进入求解模块。在Placed on右侧的下拉列表框中选择VERTEX，在图形画面中选中Point5。Output输出设置如图15-90所示。重复步骤，定义Point11、Point14处的加速度输出。设置求解需要的内存为100。End frequency：扫频终止频率为350 Hz。扫频从180～350Hz，间隔为1Hz，60r/min。Algorithm：谐波响应计算方法为Modal（模态法）。单击图标，提交作业，并显示执行状态的监视对话框。图14-92 监视对话框当计算完成后，单击Close按钮，关闭监视对话框。单击工具条中的保存文件快捷图标进行保存。......
2023-10-27
-
FEKO仿真原理与工程应用：电参数设置及近场详细阅读
图10-132 设置工作频率求解设置：展开“Configuration specific”结点，选中“Requests”并单击鼠标右键，选择“Near fields”选项，弹出“Request near fields”对话框，进行如下设置。图10-133 近场求解设置添加比吸收率：进入“Request”菜单，在“Solution requests”中单击“SAR”按钮，弹出“Request SAR”对话框，设置10g比吸收率，具体设置如下。Select calculation：Spatial-peak SAR of a 10g cube。单击“Add”按钮，继续设置。Specify the search region：Entire model。单击“Create”按钮，如图10-135所示。......
2023-10-31
-
流体域前处理及求解详细阅读
回到Workbench工作界面，双击G2进入CFX前处理界面，图5.2-14所示为轴流泵全流场。图5.2-16 基本设置图5.2-17 流体属性设置5）用步骤3）和步骤4）的参数对出口、导叶进行相同的设置。进口设置为质量流，出口设置为开放压力及方向，具体如图5.2-22、图5.2-23所示。图5.2-22 进口边界条件设置图5.2-23 出口边界条件设置图5.2-24 求解器控制11）求解。由于本章节主要介绍单向流固耦合，并不需要对流体域的结果进行后处理，所以当求解完毕之后关闭求解器，返回Workbench工作界面。......
2023-06-26
-
激光多普勒流速计的应用原理与构造详细阅读
激光测流速应用得最多的是激光多普勒流速计，它可以测量火箭燃料的流速、飞行器喷射气流的速度、风洞气流速度以及化学反应中粒子的大小及会聚速度等。激光多普勒流速计的基本原理如图6-55所示。激光测流速是基于多普勒原理。图6-55 激光多普勒流速计原理图流速计主要包括光学系统和多普勒信号处理两大部分。......
2023-06-28
-
求解：SAMCEF有限元分析应用实例详细阅读
设置工作目录，浏览并选择目录D：\Samwork。设置求解需要的内存为100。将Problem name设置为super-element.dat。选择Creation Parameters选项卡。在Number of Eigen Values文本框中输入特征值数10。选中Maximum Frequency复选框，设置为最大扫频频率3.6e3Hz。图14-138 求解设置一般情况下，最大频率应为转子工作频率的两倍。选中Condensation Algorithm复选框，选择凝结算法为Component Mode。单击图标，提交作业，并显示执行状态的监视对话框。再次单击Close按钮，关闭Solver Launch对话框。单击工具条中的保存文件快捷图标进行保存。......
2023-10-27
-
SAMCEF有限元分析、应用实例：求解详细阅读
单击Check图标，如果出现No data incoherence detected，表明数据已经定义完整，不缺少数据。单击Close按钮返回。单击Convert and Launch图标，进入求解设置对话框，如图16-49所示。图16-49 求解设置对话框设置求解需要的内存为200。单击Egien Values&Sweeping标签，进入特征值选项卡。Number Of Steps：输入15。Number of Eigen Values：输入特征值数4。单击图标，提交作业，并显示执行状态的监视对话框。当计算完成后，单击Close按钮，关闭监视对话框和Solver Launch对话框。单击工具条中的保存文件快捷图标保存文件。......
2023-10-27
相关推荐