《普通高中数学课程标准(2017年版)》指出:数据分析是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的素养.【案例6_5】获取研究的基本数据并据此进行一定的预测问题:改革开放40年,我国卫生事业取得巨大成就,卫生总费用增长了数十倍.卫生总费用包括个人现金支出、社会支出、政府支出,表6-9为2012—2015年我国卫生费用中个人现金支出、社会支出、政府支出的费......
2023-08-17
利用计算器收集和整理离散性数据,把这些数据进行直角坐标系描点处理,根据这些点列分析其几何特征,再根据这些离散的点列几何特征,概括猜想连续函数的性质,并利用所学知识进行论证,形成关于此类函数的完整性质.
【案例6-1】利用数学分析解不等式
![]()
问题1:设函数,则使得f(x)>f(3-2x)成立的x的取值范围是.
分析 已知函数f(x)的表达式,求不等式f(x)>f(3-2x)的解集.如果直接把3-2x代入f(x)解不等式,计算量较大,甚至不易求解.
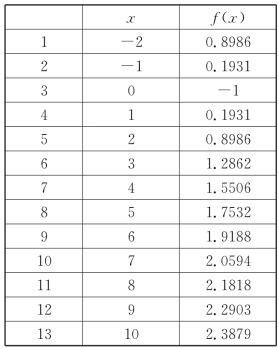
知识与技能 考查函数f(x)一定要考查函数的性质.一种方法是根据题目要考查的内容选择适当函数的性质,如定义域、值域、奇偶性、单调性、对称性、周期性、最值、零点等进行研究,再根据这些性质,求解不等式f(x)>f(3-2x);另一种方法是利用CASIO fx-991CN中文版计算器(见图6-1),按菜单,选7,进入表格功能,输入函数![]() ,按右下角“=”,显示g(x)=.若输入函数g(x),则会列出两个函数f(x)、g(x)的函数值,此题只有一个函数,就不需要.若再次按右下角“=”,显示表格范围,开始值为-2,终止值为10,步长为1.按右下角“=”,计算器就显示出函数f(x)的函数值,见表6-1.
,按右下角“=”,显示g(x)=.若输入函数g(x),则会列出两个函数f(x)、g(x)的函数值,此题只有一个函数,就不需要.若再次按右下角“=”,显示表格范围,开始值为-2,终止值为10,步长为1.按右下角“=”,计算器就显示出函数f(x)的函数值,见表6-1.

图6-1
表6-1
思维与表达 根据表6-1中的数据绘制点列图,并用光滑的曲线连接起来,如图6-2所示.图6-2反映了当x是正数时函数f(x)的函数值随着x的取值增大而增大,且x取互为相反数时,其函数值相等.
交流与反思 通过部分点列,我们是否可猜想函数f(x)是定义域为R的偶函数,且在x∈[0,+∞)上是增函数?
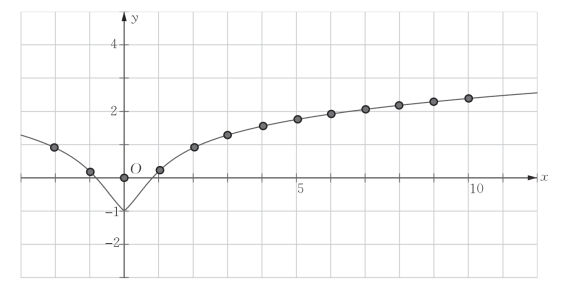
图6-2
通过前期的点列计算的猜想,再探究严谨的推理论证.因为f(-x)=f(x),所以f(x)为偶函数;当x∈[0,+∞)时,y=|x|,y=x2为增函数,所以y=ln(1+|x|)为增函数,y=![]() 为减函数,且函数值为正,所以
为减函数,且函数值为正,所以![]() 为增函数,故
为增函数,故![]() 在[0,+∞)上为增函数.
在[0,+∞)上为增函数.
从而不等式f(x)>f(3-2x)即为|x|>|3-2x|,解得1<x<3.
有关高中数学核心素养的文章

《普通高中数学课程标准(2017年版)》指出:数据分析是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的素养.【案例6_5】获取研究的基本数据并据此进行一定的预测问题:改革开放40年,我国卫生事业取得巨大成就,卫生总费用增长了数十倍.卫生总费用包括个人现金支出、社会支出、政府支出,表6-9为2012—2015年我国卫生费用中个人现金支出、社会支出、政府支出的费......
2023-08-17

数据分析随着行业的不同有一定差异性,总的来说分为列表法和作图法.列表法是将实验数据按一定规律用列表方式表达出来,是记录和处理实验数据最常用的方法.表格的设计要求对应关系清楚、简单明了、有利于发现相关量之间的物理关系;此外还要求在标题栏中注明物理量名称、符号、数量级和单位等;根据需要还可以列出除原始数据以外的计算栏目和统计栏目等.最后还要求写明表格名称、主要测量仪器的型号、量程和准确度等级、有关环境......
2023-08-17

《普通高中数学课程标准(2017年版)》指出:通过高中数学课程的学习,学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”).【案例6-7】问题:为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A、B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液,每组小鼠给服的溶液体积相同、摩尔浓度相同.经过一段......
2023-08-17

,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P,b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.①证明:{pi+1-pi}(i=0,1,2,…......
2023-08-17

《普通高中数学课程标准(2017年版)》指出:数据分析是研究随机现象的重要数学技术,是大数据时代数学应用的主要方法,也是“互联网+”相关领域的主要数学方法,数据分析已经深入到科学、技术、工程和现代社会生活的各个方面.通过高中数学课程的学习,学生能提升获取有价值信息并进行定量分析的意识和能力;适应数字化学习的需要,增强基于数据表达现实问题的意识,形成通过数据认识事物的思维品质,积累依托数据探索事物本......
2023-08-17

通过图形的表征与变换,理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化,都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.【案例4-15】构造几何模型,破解思维瓶颈问题:设点P是函数的图像上的任意一点,点Q(2a,a-3),(a∈R),则|PQ|的最小值为__________.解:函数的图像是以C(1,0)为圆心,半径等于2的圆在x轴以下的半圆,含点(-1,0)、(3,0).......
2023-08-17

(一)抽象1.理想化的抽象理想化的抽象即指抽象层次性的简约阶段,由实际的事物或现象引出抽象概念的方法,其中包括对于真实事物或现象的简约化与完善化,从而得出的数学概念与现实原型未必完全符合,如“没有大小的点”“没有宽度的线”“没有厚度的面”等几何概念都是简约化的结果.平面几何中已经证明任意三角形三个角的平分线交于一点,但真实世界的经验告诉我们,无论绘图员多么细心、采用多么精确的工具,他所画图形中的三......
2023-08-17

2016年,教育部考试中心构建了高考评价体系框架,明确“必备知识、关键能力、学科素养、核心价值”的考查目标以及“基础性、综合性、应用性、创新性”的考查要求.在推动核心素养在基础教育中落地生根的关键阶段,高考毋庸置疑是最现实、最立竿见影的途径之一.上海每年高考数学试题,在上一年试点改革成功的基础上,继续巩固改革成果,近几年还适当降低压轴题的难度,贴近广大考生的水平.试卷中彰显学科特点,发挥了数学培养......
2023-08-17
相关推荐