，8）表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1（i=1，2，…，7），其中a=P，b=P（X=0），c=P（X=1）.假设α=0.5，β=0.8.①证明：{pi+1-pi}（i=0，1，2，…......
2023-08-17
数学建模素养检查：思维品质分析
【摘要】：对于刚刚接触数学建模的教师，常常把简单的“文字应用题”看成是“数学建模”，这类问题情境常常是条件不多不少，解法指向清晰，结果常常是确定的或唯一的.而数学建模常常需要一般化地解决一类问题，初始条件的变动会给解决问题的模型带来随参数变动的不同结果，是思维品质的常用考查方式之一.建立数学模型，要求学生发掘问题的内在联系，抽象问题的本质，进而用数学语言正确表达问题实质.数学建模的过程，是学生全面思考、分析
对于刚刚接触数学建模的教师，常常把简单的“文字应用题”看成是“数学建模”，这类问题情境常常是条件不多不少，解法指向清晰，结果常常是确定的或唯一的.而数学建模常常需要一般化地解决一类问题，初始条件的变动会给解决问题的模型带来随参数变动的不同结果，是思维品质的常用考查方式之一.
建立数学模型，要求学生发掘问题的内在联系，抽象问题的本质，进而用数学语言正确表达问题实质.数学建模的过程，是学生全面思考、分析问题的过程，是培养学生思维的深刻性和创造性的必要手段.
【案例5-7】两山顶M、N间的距离多远
图5-28
问题：为了测量两山顶M、N间的距离，飞机沿水平方向在A、B两点进行测量，A、B、M、N在同一个铅垂平面内，如图5-28所示.飞机能够测量的数据有俯角和A、B间的距离，请设计一个方案，包括：①指出需要测量的数据（用字母表示，并在图中标出）；②用文字和公式写出计算M、N间的距离的步骤.
方案一 ①需要测量的数据有：A点到M、N点的俯角α1、β1；B点到M、N的俯角α2、β2；A、B的距离d.
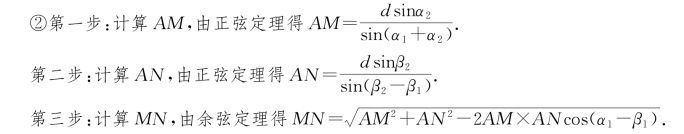
方案二 ①需要测量的数据有：A点到M、N点的俯角α1、β1；B点到M、N的俯角α2、β2；A、B的距离d.
从案例5-7中可以看出，数学源于生活实践，最终也将应用于生活，数学的知识必将对生活中的事实给出完美的理论解释.
注重知识横向和纵向的联系，把握知识、方法、思想之间的联系，置知识于系统之中，让所学知识牢不可破.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：思维品质与数学抽象判断详细阅读
在高考试题中考查数学的思维策略与方法是近几年的热点之一.而高考中突出考查思维策略与方法有一般与特殊、正向与逆向的转化方法的灵活应用.从数学的解题方法上，能掌握相应的思维策略与方法，常常使人茅塞顿开、绝处逢生.（一）一般化思维方法一般化是与特殊化相反的思维方法，即将研究对象从原来范围扩展到更大范围进行考察和研究.由一个特殊性问题，联想到它的一般性问题，然后通过对一般性问题的分析、研究，来使特殊性问题......
2023-08-17
-
高中数学核心素养：直观想象能力的思维品质研究详细阅读
直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.【案例4-13】利用几何直观形成论证思路问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.图4-29分......
2023-08-17
-
高中数学建模核心素养详细阅读
数学模型是用数学符号、函数关系将评价目标和内容系统规定下来，并把互相间的变化关系通过数学公式表达出来，这一过程就是数学建模的过程.数学建模作为问题解决的一种模式，体现了一个学生对原始问题的分析、假设和抽象的数学加工过程，是学生归纳理解以及创新能力的综合表现.数学模型教学能够能动地让学生用所学的数学必备知识去解决问题，能够培养学生对所学知识的“想用、能用、会用”的数学意识.试题中数学建模思想的意蕴解......
2023-08-17
-
高中数学核心素养：理解数学建模详细阅读
“数学建模”中“数学”是“建模”的限制词，因此需要先考察“建模”，“建模”中，动词“建”指建立、建构或者构造；名词“模”指模型，因此建模就是建立模型或者建构模型的意思.（一）模型《辞海》（2009）对“模型”一词有3项释义.（1）与“原型”相对研究对象的替代物原型，即客观存在的对象客体；模型是具有原型相似特征的替代物，是系统或过程的简化、抽象或类比表示.（2）根据实物、设计图或设想，按比例、形态或......
2023-08-17
-
数学运算素养：培养思维，提升核心素养详细阅读
思维是指理性认识的过程，是人脑对客观事物间接的和概括的反映，属于人脑的基本活动形式.数学思维则是指用数学思考问题和解决问题的思维活动形式.数学思维既能动地反映客观世界，又能动地反作用于客观世界.数学运算中强调探究运算思路，通过探究可以激发思维的灵活性、广阔性，锻炼思维的敏捷性和深刻性，形成思维的独创性、批判性和灵活性.问题：书架上有5本书，现在再插入3本不同的书，有多少种不同的方案？......
2023-08-17
-
提升高中数学核心素养：简单数学游戏辅助数学建详细阅读
苏联教育家马卡连柯曾说过：“游戏在儿童生活中具有重要的意义，具有与成人活动、工作和劳动同样重要的意义.”游戏本身具有愉快、自由及探索的特性，游戏是孩子们的天性，也是认识世界的途径之一，其不但可以满足学生的好奇心理，还能有效培养他们各方面的能力.如今数学建模的教学课堂普遍枯燥乏味，而简单的数学游戏能够通过创设一个游戏化的场景让学生更加放松，从而让学生对于传统教学模式不那么排斥，可以更有效地理解数学概......
2023-08-17
-
高中数学建模素养的认知价值详细阅读
数学建模就是要培养学生用事物相互联系和发展变化的观点来分析问题，从而认识事物之间是相互联系和有规律地变化着的.数学建模是数学与其他领域之间建立联系的方法.数学建模的过程就是提出一个问题，然后细化问题，最后以精确的数学术语表述.一旦问题变成数学问题，就要使用数学来找到答案，并且最后必须逆转这一过程（这是很多人忘记的部分），将数学解转换回对原始问题的可理解的，有意义的答案.从思想上来说，数学建模是构建......
2023-08-17
相关推荐