《普通高中数学课程标准（2017年版）》指出：数据分析是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养.【案例6_5】获取研究的基本数据并据此进行一定的预测问题：改革开放40年，我国卫生事业取得巨大成就，卫生总费用增长了数十倍.卫生总费用包括个人现金支出、社会支出、政府支出，表6-9为2012—2015年我国卫生费用中个人现金支出、社会支出、政府支出的费......
2023-08-17
高中数学核心素养详解
【摘要】：通过图形的表征与变换，理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化，都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.【案例4-15】构造几何模型，破解思维瓶颈问题：设点P是函数的图像上的任意一点，点Q（2a，a-3），（a∈R），则|PQ|的最小值为__________.解：函数的图像是以C（1，0）为圆心，半径等于2的圆在x轴以下的半圆，含点（-1，0）、（3，0）.
通过图形的表征与变换，理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化，都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.
【案例4-15】构造几何模型，破解思维瓶颈
问题：设点P是函数
的图像上的任意一点，点Q（2a，a-3），（a∈R），则|PQ|的最小值为__________.
解：函数
的图像是以C（1，0）为圆心，半径等于2的圆在x轴以下的半圆，含点（-1，0）、（3，0）.点Q（2a，a-3）（a∈R）为直线l：x-2y-6=0上的动点，所以，|PQ|的最小值等于圆心C（1，0）到直线l：x-2y-6=0的距离d减去圆的半径r，即d-r=
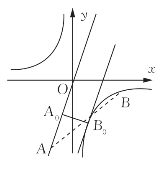
图4-32
变式：已知a=3c，bd=-3，求（a-b）2+（d-c）2的最小值.
解：根据题意，点A（a，c）是直线y=3x上的动点，点B（b，d）是曲线
上的动点，所以（a-b）2+（d-c）2=|AB|2，如图4-32所示，将直线y=3x平移，假设与曲线
相切于点B0，过B0作直线y=3x的垂线，设垂足为A0，则|AB|2的最小值等于|A0B0|2，即点B0到直线y=3x的距离（点线距离）的平方.设B0（x0，y0），由y=-
，得
解得B0（1，-3）或B0（-1，3）.
从案例4_15中可以看出，数形结合是基本的数学思想方法，面对某些“代数”问题，如果直接去解，运算难度大，甚至难以得到结果，这时，我们会尝试挖掘问题的几何背景，构造恰当的几何模型，然后借助几何模型思考，通常可以破解思维的瓶颈，克服运算的障碍，化难为易，使问题顺利得到有效解决.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：抽象素养与其他素养考查指南详细阅读
2016年，教育部考试中心构建了高考评价体系框架，明确“必备知识、关键能力、学科素养、核心价值”的考查目标以及“基础性、综合性、应用性、创新性”的考查要求.在推动核心素养在基础教育中落地生根的关键阶段，高考毋庸置疑是最现实、最立竿见影的途径之一.上海每年高考数学试题，在上一年试点改革成功的基础上，继续巩固改革成果，近几年还适当降低压轴题的难度，贴近广大考生的水平.试卷中彰显学科特点，发挥了数学培养......
2023-08-17
-
高中数学核心素养：数学抽象素养的扩展详细阅读
（一）抽象1.理想化的抽象理想化的抽象即指抽象层次性的简约阶段，由实际的事物或现象引出抽象概念的方法，其中包括对于真实事物或现象的简约化与完善化，从而得出的数学概念与现实原型未必完全符合，如“没有大小的点”“没有宽度的线”“没有厚度的面”等几何概念都是简约化的结果.平面几何中已经证明任意三角形三个角的平分线交于一点，但真实世界的经验告诉我们，无论绘图员多么细心、采用多么精确的工具，他所画图形中的三......
2023-08-17
-
培养创造能力：高中数学核心素养详细阅读
探究7：若将焦点F改为点F2，对应准线改为直线=1，则圆、椭圆是否具有组合1、2、3的性质？事实上，点F2是直线l的极点，直线l是点F2的极线.给定圆或圆锥曲线Γ，当极点在Γ内时，其对应的极线与Γ相离；当极点在Γ上时，其对应的极线与Γ相切；当极点在Γ外时，其对应的极线与Γ相交.由极点和对应的极线，可得一系列的调和点列.......
2023-08-17
-
提升高中数学核心素养详细阅读
美国的科普学家马丁·加德纳（Martin Gardner）认为，在数学教育的过程中要想避免那些没有价值并且枯燥的东西，老师就需要给学生提供一些有趣的智力题或是游戏性的教学，另外也可以提供一些比较搞笑的笑话或是悖论，这些都可以调动学生学习的积极性，唤醒学生的学习欲望.这样就肯定了数学游戏在高中数学教学中的作用.数学知识的抽象性和逻辑性决定了数学课堂的枯燥和无味，但随着素质教育的不断推进，数学课堂也在......
2023-08-17
-
高中数学核心素养考试指南详细阅读
《普通高中数学课程标准（2017年版）》还将数学建模的学业质量划分成递进的3个水平，通过4个方面进行描述，即情境与问题、知识与技能、思维与表达、交流与反思.这4个方面对应必修课程结束、选择性必修课程结束时对学生数学建模素养的达成提出的要求，是学业质量的主要内容.数学建模素养的水平描述如下.水平一（1）情境与问题.了解熟悉的数学模型的实际背景及其数学描述，了解数学模型中的参数、结论的实际含义.（2）......
2023-08-17
-
高中数学建模核心素养详细阅读
数学模型是用数学符号、函数关系将评价目标和内容系统规定下来，并把互相间的变化关系通过数学公式表达出来，这一过程就是数学建模的过程.数学建模作为问题解决的一种模式，体现了一个学生对原始问题的分析、假设和抽象的数学加工过程，是学生归纳理解以及创新能力的综合表现.数学模型教学能够能动地让学生用所学的数学必备知识去解决问题，能够培养学生对所学知识的“想用、能用、会用”的数学意识.试题中数学建模思想的意蕴解......
2023-08-17
-
高中数学核心素养-数据分析详细阅读
数据分析随着行业的不同有一定差异性，总的来说分为列表法和作图法.列表法是将实验数据按一定规律用列表方式表达出来，是记录和处理实验数据最常用的方法.表格的设计要求对应关系清楚、简单明了、有利于发现相关量之间的物理关系；此外还要求在标题栏中注明物理量名称、符号、数量级和单位等；根据需要还可以列出除原始数据以外的计算栏目和统计栏目等.最后还要求写明表格名称、主要测量仪器的型号、量程和准确度等级、有关环境......
2023-08-17
相关推荐