高中数学核心素养：直观想象能力的思维品质研究

2025-09-29 理论教育版权反馈

【摘要】：直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.【案例4-13】利用几何直观形成论证思路问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.图4-29分

直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.

【案例4-13】利用几何直观形成论证思路

问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.

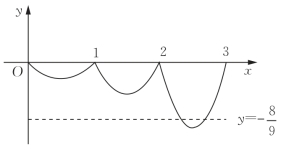
pagenumber_ebook=121,pagenumber_book=112

图4-29

分析此题能较好地考查学生关于函数概念、函数与不等式的关系，以及建立几何模型和借助几何模型解决问题的能力.由f（x+1）=2f（x）可知，f（x）图像每向右平移1个单位，图像上点的纵坐标扩大为原来的2倍，如图4-29所示.由x∈（0，1]时，f（x）=x（x-1）知，x∈（1，2]时，f（x）∈时，f（x）∈[-1，0]，故m∈（2，3].

pagenumber_ebook=121,pagenumber_book=112 (https://www.chuimin.cn)

此题思维的难点与关键在于如何把握图形的变化规律及图形背后所蕴含的数量关系，是借助几何直观形成解题思路.

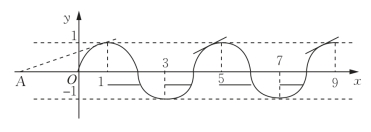
pagenumber_ebook=122,pagenumber_book=113

图4-30

分析此题能较好地考查学生的周期函数、分段函数等概念，以及建构几何模型和借助几何模型解决问题的能力.由于此题是关于方程根的个数问题而不是根的大小问题，并且从方程f（x）=g（x）有8个不同的实数根可知，单纯从“数”的视角考虑可能难以解决问题，应先从“形”的视角搞清楚方程根的大致分布情况.由，x∈（0，2]可得（x-1）2+y2=1，（y＞0）.由f（x）是奇函数且它的周期为4，得知它在区间（0，9]上的图像如图4-30所示，由题意，f（x）与g（x）的图像有8个交点，而x∈（1，2]∪（3，4]∪（5，6]∪（7，8]时，f（x）与g（x）的图像有6个交点.由f（x）与g（x）的周期性知，x∈（0，1]时，f（x）与g（x）的图像有2个交点，即线段y=k（x+2），（0＜x≤1）与圆弧（x-1）2+y2=1，（0＜x≤1，y≥0）有2个交点.因此，点（1，0）到直线y=k（x+2）的距离小于1，且g（1）≥f（1），解得 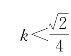pagenumber_ebook=122,pagenumber_book=113 ，即k的取值范围是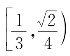

此题的难点在于如何利用已知条件建立几何直观和利用几何直观形成解题思路，是如何通过“看”寻找解题思维的突破口.搞清楚f（x）与g（x）图像之间的关系，具体运算只是小事一桩.

高中数学核心素养：直观想象能力的思维品质研究

相关推荐