为方便起见，取a=10，则问题转化为：是否存在m、n＞0，使lg（m+n）=lgm·lgn成立？......
2023-08-17
提升高中数学核心素养：图形计算器辅助直观想象
【摘要】：图形计算器作为研究数学问题的一个工具，能够在学生开展数学学习的过程中提供一定的辅助作用.尤其是它在通过函数图像研究函数性质、解析几何的问题研究方面，能通过直观而动态的变化，方便学生更好地理解问题的本质.【案例4-10】用TI图形计算器解一道解析几何压轴题问题：已知椭圆=1（a＞b＞0），半焦距为c（c＞0），且满足（2a-3c）+（a-c）i=i（其中i为虚数单位），经过椭圆的左焦点F（-c，0）
图形计算器作为研究数学问题的一个工具，能够在学生开展数学学习的过程中提供一定的辅助作用.尤其是它在通过函数图像研究函数性质、解析几何的问题研究方面，能通过直观而动态的变化，方便学生更好地理解问题的本质.
【案例4-10】用TI图形计算器解一道解析几何压轴题
问题：已知椭圆
=1（a＞b＞0），半焦距为c（c＞0），且满足（2a-3c）+（a-c）i=i（其中i为虚数单位），经过椭圆的左焦点F（-c，0），斜率为k1（k1≠0）的直线与椭圆交于A、B两点，O为坐标原点.
（1）求椭圆的标准方程；
（2）当k1=1时，求S△AOB的值；
（3）设R（1，0），延长AR、BR分别与椭圆交于C，D两点，直线CD的斜率为k2.求证：
为定值.
利用TI的解决方案：
（1）如图4-19所示，利用解方程组功能解出a，b，考虑到a＞0，b＞0，得a=3
，所以椭圆Γ的方程为
图4-19
（2）接着，在页面1.2中作椭圆
，直线y=x+2，并交椭圆于A、B两点，构造三角形OAB，并测量面积为3.03，如图4-20所示.
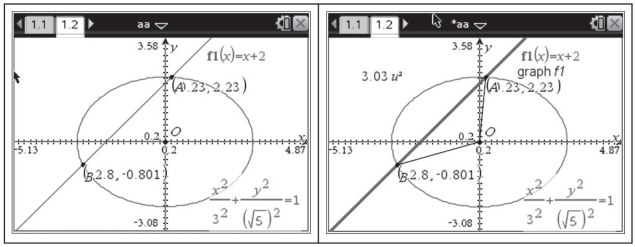
图4-20
实际操作非常简单，但是，这样做的结果并不是一个精确值，于是，我们尝试求出AB的长度以及O点到AB的距离，再进行计算.回到页面1.1，通过解方程组将两个交点A、B的坐标解出来，再计算出AB的长度为
，如图4-21所示.
图4-21
下面我们作O到AB的距离，先过O点作AB的垂线得到垂足C，测量OC距离得1.41.再计算面积得3.02143，如图4-22所示.
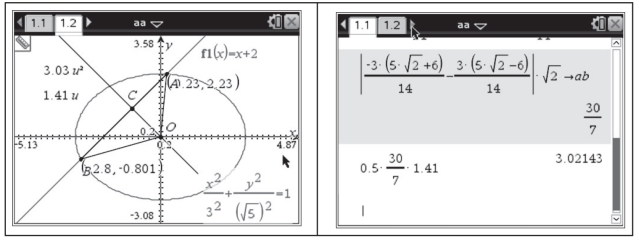
图4-22
图4-23
对比发现，这仍然不是一个精确值，问题在于OC的距离，为了能得到更精确的值，我们试着通过求直线方程来解决.因为直线OC与直线AB垂直并且过原点，所以直线OC的方程为y=-x，接着求两直线的交点，即解方程组得C点坐标为（-1，1），这样OC距离为
就显而易见了.再计算面积得
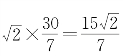，这样我们终于得到了一个精确值，如图4-23所示.
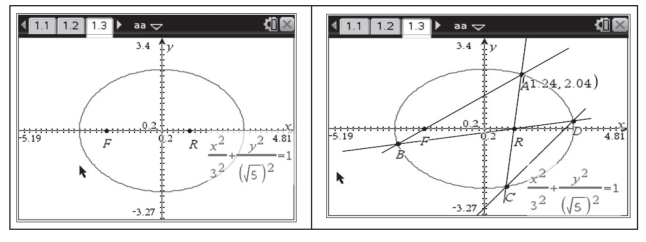
图4-24
（3）在页面1.3作椭圆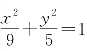
，取点F、点R.在椭圆上取动点与点F连接构成直线交椭圆于A、B两点，连接AR延长交椭圆于点C，连接BR延长交椭圆于点D，连接直线CD.分别测量直线AB和CD的斜率记为k1和k2，计算k1与k2的比值，拖动椭圆上的动点改变两条直线的斜率，发现随着动点在椭圆上移动，两条直线的斜率会有变化，但比值不变，始终是0.571，如图4-24所示.虽然它仍然是一个近似值，不过我们得到了一个直观的认识，就是这个比值不会因为k1的变化而变化，它始终是一个定值，如图4-25所示.
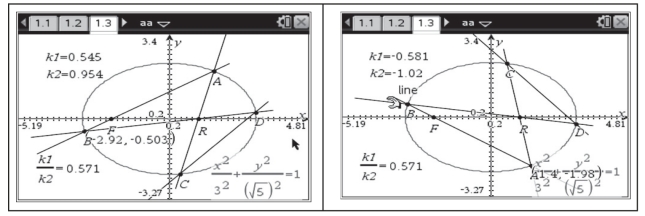
图4-25
更进一步，也可以参照常规解法，利用图形计算器的解方程功能将k1和k2用x1，y1、x2，y2表示，最终得到比值为一个定值.
从案例4-10中可以看出，信息技术在教学中的优势主要表现在：快捷的计算功能、丰富的图形呈现与制作功能、大量数据的处理功能；提供交互式的学习和研究环境等方面.因此，在教学中，应重视数学教学与现代信息技术的有机结合，恰当地使用现代信息技术，发挥现代信息技术的优势，帮助学生更好地认识和理解数学，增强学生对数学学习的兴趣，同时也提高几何直观和空间想象的能力.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：图形计算器辅助提升数学抽象详细阅读
20世纪90年代，美国德州仪器（Texas Instruments，TI）等专业技术生产企业开始逐渐扩大市场规模，带着不同类型的图形计算器产品叩开了中国学校的大门.图形计算器是一款集数据处理、方程解析、图表绘制、模型建立等多种功能于一身的新型手持学习工具，为数理化等学科的课堂教学带来了深刻的变化.2010年，TI依靠强大的技术团队，成功构建了TI-Nsipre图形计算器和无线数学实验室，帮助很多学......
2023-08-17
-
高中数学核心素养：图形计算器辅助推理技巧提升详细阅读
图形计算器作为研究数学问题的一个工具，能够在学生开展数学学习的过程中提供过一定的辅助作用.尤其是它在作函数图像上的操作简便性，为学生从众多特殊情况中归纳和抽象出问题本质，并在此基础上进行演绎证明，提供了很好的帮助.【案例3-15】借助函数图像研究函数性质问题1：函数y=loga x的相关性质.如图3-3所示，利用动态图展示函数图像，能够明确当底数a取不同值时，函数单调性的变化，也能够明确无论底数如......
2023-08-17
-
高中数学核心素养：简单数学游戏辅助直观想象提详细阅读
人们对数学有一个严重的误解，认为它只是枯燥无味的计算.这种观点完全是错误的，事实上，数学是关于想象力、洞察力和直觉的学科，真正的数学灵感正是来自这三者.数学是抽象游戏的集合，是科学，也是一种看待事物的角度.在这个抽象规则构成的数学游戏小世界里，有精彩的解题思路、巧妙的解题技巧、标准的序列、有力的方法、熟悉的布阵、致胜的奇招和杰出的组合等.【案例4-11】用复数找宝虚数闯进数学领地之后，足足有几个世......
2023-08-17
-
提升高中数学核心素养：图形计算器辅助数学建模详细阅读
图5-17分析第一步面对这一景区建造人行道的实际问题，首先需要学生在引导下抽象成数学问题：已知一个正五边形A1A2A3A4A5，边长为10cm，点P、Q分别为边A1A2、A2A3、A3A4、A4A5、A5A1上任意两个动点，则P、Q两动点间距离的最大值为多少？......
2023-08-17
-
高中数学核心素养-考查直观想象能力详细阅读
直观想象在数学核心素养体系中具有重要的地位，与其他数学学科核心素养密不可分.在复杂情境中发现问题、解决问题，通常需要先通过直观想象对问题进行分析、探寻问题实质，再通过数学抽象、数学建模将其转化为数学问题.在复杂的逻辑推理或数学运算中，也需要运用直观想象来理清思路、简化运算；在大数据分析时，有时也要借助图表使数据更加直观.【案例4-14】把数学问题直观化、图形化问题：在平面四边形ABCD中，∠ADC......
2023-08-17
-
高中数学核心素养：使用动态教学软件提升直观想详细阅读
在函数概念、指数函数、对数函数、三角函数、统计、立体几何初步、曲线与方程等内容中，课程标准明确建议借助计算器或计算机进行教学.这就需要我们深入研究包括这些内容在内的数学教学中，如何恰当地使用信息技术，帮助学生理解和掌握知识、增强学习兴趣、改善学习方式.【案例4-12】模拟撒豆试验计算π的近似值人类对圆的探索，可以追溯到上古时期，尽管圆有大有小，但圆的周长l与直径d之间存在着比例常数圆周率π.公元前......
2023-08-17
-
高中数学核心素养：培养思维，直观想象价值详细阅读
问题6：怎样用棱数E和面数F表示多面体所有多边形的内角和？在假设多面体的F个面分别是n1，n2，n3，…图4-7中所有多边形的内角和是.图4-7案例4-4中，采用降维思想和转化策略将空间问题转化为平面问题来研究，这种处理问题的方法是立体几何中的重要思想方法，在降维和升维（如翻折）过程中关健要弄清不变量与变量.从案例4-4中可以看到，转化策略是解决数学问题的主要方法之一，如何转化是关健.......
2023-08-17
相关推荐