《普通高中数学课程标准（2017年版）》对培养学生直观想象素养的要求体现在多个方面.比如，在必修课程与选择性必修课程中，突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联，加强对数学整体性的理解.必修课程如图4-11所示，选择性必修课程如图4-12所示.图4-12在必修课程中，从函数观点看一元二次方程和一元一次不等式的教学，让学生逐渐养成借助直观理解概念的习惯.在三角函数......
2023-08-17
高中数学核心素养：直观想象在教学活动中的渗透
【摘要】：在数学素养的生成教学策略上，许多国家都倡导用数学活动促进学生数学素养的生成.不少专家提倡，数学学习活动应当具有愉快感和充实感，能体现学生学习过程中的多样性和个性化，给予学生更多的自由发展空间.立体几何序言课课堂实录师：请同学们用6根长度相等的牙签（或火柴）搭正三角形，试试看，最多搭成几个正三角形？
在数学素养的生成教学策略上，许多国家都倡导用数学活动促进学生数学素养的生成.不少专家提倡，数学学习活动应当具有愉快感和充实感，能体现学生学习过程中的多样性和个性化，给予学生更多的自由发展空间.
【案例4-8】立体几何序言课
课堂实录
师：请同学们用6根长度相等的牙签（或火柴）搭正三角形，试试看，最多搭成几个正三角形？
生1：开始在桌面上摆，有的摆成两个余下一根牙签；有的在桌面上摆成塔形，塔底为三角形，出现4个三角形.学生兴趣很浓，积极探索摆法，最后都探索到，在空间，可搭成四个正三角形.
师：在平面内（桌面）最多只能搭成两个，而在空间能搭成四个正三角形.
同时，向学生展示正四面体骨架模型，再让学生看图4-13（a）所示的图形.
师：请同学们想一想，是否存在3条直线两两互相垂直的情况？若存在，请举出实际中的例子.
生2：有的在纸上画；有的用笔、直尺等演示；有的在教室四周观察.议论纷纷，有的说不存在，有的说存在，各持己见，争论不休.
师：在两种不同意见的学生中各选一人，让他们陈述理由.
生3：不存在.因为若a⊥c，b⊥c，则a∥b.
生4：存在.如教室墙角处的三条直线两两互相垂直.
师：在同一平面内不存在，如生3的理由；但在空间是存在的，如生4同学所举的实例，教室墙角处的3条直线AB、AC、AD两两互相垂直，见图4-13（b）.请同学们观察正方体（向学生展示正方体模型）中一个顶点处的3条棱之间的关系，也是两两互相垂直的，见图4-13（c）.
师：现实世界中许多问题，只在平面内研究是很不够的，还需要在空间这个更广阔的领域内来考虑和研究，这就是我们将要学习的“立体几何”.
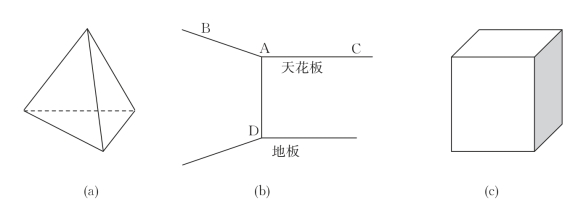
图4-13
案例4-8中，课程的引入从学生已有的平面几何知识入手，利用模型和投影图形，启发、引导学生积极探索，大胆实践，极大地激发了学生学习的积极性和创造性，使抽象的序言课上得具体、生动，内容丰富.既使学生获得了知识，又培养了学生的能力.为学生学习立体几何创造了良好的开端，成功地拉开了立体几何教学的帷幕.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：数学建模在教学活动中的渗透详细阅读
基于数学核心素养的教学就是要培养学生用数学的眼光看世界，因此，数学教师首先要能够用数学的眼光看世界，用数学的眼光看身边的事物，并在平时教学中能够注重基于教学内容的实际背景向学生渗透数学与实际生活的联系.（一）数学建模的教学原则数学建模活动作为《普通高中数学课程标准（2017年版）》课程内容之一，要求以课题形式，小组合作方式开展教学，最终以研究报告或小论文等多种形式呈现.数学建模活动的主要特征体现在......
2023-08-17
-
高中数学学习中直观想象核心素养的渗透详细阅读
同学们通过积极的讨论，提出各种问题及想法大致为如下几个方面.在长方体中，展开方式的不同将影响最小路径的求解，值得注意.几何体表面路径问题与两点间的距离的关系.“蜘蛛路径问题”的方法，是否可以推广.几何体表面路径最值问题求解的思想方法.几何体是否都能够把表面展开？......
2023-08-17
-
高中数学核心素养-考查直观想象能力详细阅读
直观想象在数学核心素养体系中具有重要的地位，与其他数学学科核心素养密不可分.在复杂情境中发现问题、解决问题，通常需要先通过直观想象对问题进行分析、探寻问题实质，再通过数学抽象、数学建模将其转化为数学问题.在复杂的逻辑推理或数学运算中，也需要运用直观想象来理清思路、简化运算；在大数据分析时，有时也要借助图表使数据更加直观.【案例4-14】把数学问题直观化、图形化问题：在平面四边形ABCD中，∠ADC......
2023-08-17
-
高中数学核心素养：使用动态教学软件提升直观想详细阅读
在函数概念、指数函数、对数函数、三角函数、统计、立体几何初步、曲线与方程等内容中，课程标准明确建议借助计算器或计算机进行教学.这就需要我们深入研究包括这些内容在内的数学教学中，如何恰当地使用信息技术，帮助学生理解和掌握知识、增强学习兴趣、改善学习方式.【案例4-12】模拟撒豆试验计算π的近似值人类对圆的探索，可以追溯到上古时期，尽管圆有大有小，但圆的周长l与直径d之间存在着比例常数圆周率π.公元前......
2023-08-17
-
高中数学核心素养：培养思维，直观想象价值详细阅读
问题6：怎样用棱数E和面数F表示多面体所有多边形的内角和？在假设多面体的F个面分别是n1，n2，n3，…图4-7中所有多边形的内角和是.图4-7案例4-4中，采用降维思想和转化策略将空间问题转化为平面问题来研究，这种处理问题的方法是立体几何中的重要思想方法，在降维和升维（如翻折）过程中关健要弄清不变量与变量.从案例4-4中可以看到，转化策略是解决数学问题的主要方法之一，如何转化是关健.......
2023-08-17
-
高中数学核心素养：直观想象能力的思维品质研究详细阅读
直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.【案例4-13】利用几何直观形成论证思路问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.图4-29分......
2023-08-17
-
高中数学核心素养：直观想象的认知关联价值详细阅读
提升学生直观想象核心素养，在帮助他们认知事物之间的关联方面具有非同一般的价值.通过直观想象素养的培养，帮助学生通过数学间的内在联系，将数学问题图像化，分析问题的本质关联，从而将问题理解得更为深入，问题的解决得以顺利进行.三角函数的周期性1.问题的提出“离离原上草，一岁一枯荣，野火烧不尽，春风吹又生”蕴含了什么数学知识？......
2023-08-17
相关推荐