首页理论教育培养创造能力：高中数学核心素养

培养创造能力：高中数学核心素养

2023-08-17 理论教育版权反馈

【摘要】：探究7：若将焦点F改为点F2，对应准线改为直线=1，则圆、椭圆是否具有组合1、2、3的性质？事实上，点F2是直线l的极点，直线l是点F2的极线.给定圆或圆锥曲线Γ，当极点在Γ内时，其对应的极线与Γ相离；当极点在Γ上时，其对应的极线与Γ相切；当极点在Γ外时，其对应的极线与Γ相交.由极点和对应的极线，可得一系列的调和点列.

直观想象素养的提升，对于学生创造能力方面的培养有着非常重要的作用.学生在学习过程中，通过直观表征入手，将数学问题与直观图表或者事物相联系，形成创造的基础.并在不断的变式中，形成富有创建的数学结果.

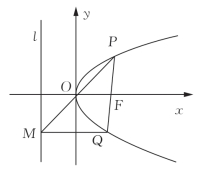
pagenumber_ebook=108,pagenumber_book=99

图4-9

【案例4_7】圆锥曲线的焦点弦问题

问题1：过抛物线焦点的一条直线与它交于两点P、Q，通过点P和抛物线顶点的直线交准线l于点M，则直线MQ平行于抛物线的对称轴.

探究1：如图4-9所示，设抛物线y2=2px（p＞0）焦点为F，顶点为O，本题题意可分成3部分：①P、F、Q共线；②P、O、M共线；③MQ平行于x.若将任意两个作为条件，是否可以导出第3个？

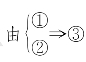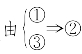组合1 pagenumber_ebook=109,pagenumber_book=100 ，此即本题.

组合2 pagenumber_ebook=109,pagenumber_book=100 ，即若经过F的直线交抛物线于P、Q两点，点M在抛物线的准线上，且MQ∥x轴，则P、O、M三点共线.

组合3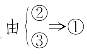 pagenumber_ebook=109,pagenumber_book=100 ，即P、Q为抛物线上的两点，过P点与抛物线顶点O的连线交准线于M点，且满足MQ∥x轴，则直线PQ过抛物线焦点F.

以上3个组合，证明皆可成立，见图4-10，此处证略.

pagenumber_ebook=109,pagenumber_book=100

图4-10

探究2：椭圆、双曲线是否具有上述3个组合的性质呢？

答案是否定的.事实上，在探究1中，点O既是抛物线的顶点，又是线段EF的中点，其中E为抛物线的准线与对称轴的交点，探究2表明：点O作为抛物线的顶点时，探究1的结论不适宜椭圆和双曲线，那么点O作为线段EF的中点，又如何？（证略）

问题2：设椭圆（双曲线）的一个（左或右）焦点为F，对应的准线为l，l与x轴交于E点，EF中点为L，过F点的直线与椭圆（双曲线）交于P、Q点，Q点在l上的射影为M，记：①P、F、Q共线；②P、L、M共线；③MQ平行于x轴.

探究3：椭圆、双曲线是否具有组合1的性质？

探究4：椭圆、双曲线是否具有组合2的性质？

探究5：椭圆、双曲线是否具有组合3的性质？

探究6：若将焦点F改为x轴上的点F1（x0，0）（在曲线内，且x0≠0），对应准线改为直线，则圆、椭圆、双曲线是否同样具有组合1、2、3的性质？

探究7：若将焦点F改为点F2（x0，y0）（在曲线内），对应准线改为直线=1，则圆、椭圆是否具有组合1、2、3的性质？

探究8：若将焦点F改为点F2（x0，y0）（在曲线内），对应准线改为直线=1，则双曲线是否具有组合1、2、3的性质？

事实上，点F2（x0，y0）是直线l的极点，直线l是点F2（x0，y0）的极线.

（1）给定圆或圆锥曲线Γ，当极点在Γ内时，其对应的极线与Γ相离；当极点在Γ上时，其对应的极线与Γ相切；当极点在Γ外时，其对应的极线与Γ相交.

（2）由极点和对应的极线，可得一系列的调和点列.