问题6：怎样用棱数E和面数F表示多面体所有多边形的内角和？在假设多面体的F个面分别是n1，n2，n3，…图4-7中所有多边形的内角和是.图4-7案例4-4中，采用降维思想和转化策略将空间问题转化为平面问题来研究，这种处理问题的方法是立体几何中的重要思想方法，在降维和升维（如翻折）过程中关健要弄清不变量与变量.从案例4-4中可以看到，转化策略是解决数学问题的主要方法之一，如何转化是关健.......
2023-08-17
高中数学核心素养：直观想象的认知关联价值
【摘要】：提升学生直观想象核心素养，在帮助他们认知事物之间的关联方面具有非同一般的价值.通过直观想象素养的培养，帮助学生通过数学间的内在联系，将数学问题图像化，分析问题的本质关联，从而将问题理解得更为深入，问题的解决得以顺利进行.三角函数的周期性1.问题的提出“离离原上草，一岁一枯荣，野火烧不尽，春风吹又生”蕴含了什么数学知识？
提升学生直观想象核心素养，在帮助他们认知事物之间的关联方面具有非同一般的价值.通过直观想象素养的培养，帮助学生通过数学间的内在联系，将数学问题图像化，分析问题的本质关联，从而将问题理解得更为深入，问题的解决得以顺利进行.
【案例4-5】三角函数的周期性
1.问题的提出
（1）“离离原上草，一岁一枯荣，野火烧不尽，春风吹又生”蕴含了什么数学知识？
（2）转动的摩天轮：任意一点P的位置转动一圈以后回到原来的位置.
（3）我们为什么只需排出一个星期的课表，而不是按日期排出每天课表？
教师引导学生分析后，再让学生找出生活中许多周而复始的例子：时钟、季节、月、日、天体运动等，体验生活中的周期性.
2.问题的研究
（1）以星期为例，解决这样一个问题，“今天是星期一，10天后将是星期几，1000天后将是星期几”，从而引出f（x+T）=f（x）的含义及应用
（2）观察三角函数线的变化规律：①正弦函数值、余弦函数值是有规律不断重复出现的；②规律是每隔2π重复出现一次（或者说每隔2kπ，k∈Z重复出现）；③这个规律由诱导公式sin（2kπ+x）=sin x，cos（2kπ+x）=cos x也可以说明.
结论：像这样的函数叫做周期函数.
3.概念的应用
问题：若钟摆的高度h（mm）与时间t（s）之间的函数关系如图4-8所示.
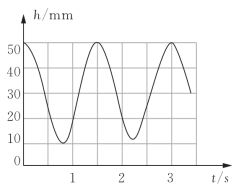
图4-8
（1）求该函数的周期；
（2）求t=10s时时钟摆的高度.
从案例4-5中可以看出，数学源于生活，高于生活.在教学中，借助生活情境，通过具体现象能让学生通过观察、类比、思考、交流、讨论，感知周期现象的存在，深入浅出地阐明周期性.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：认知事物间的关联价值详细阅读
表征性抽象，时常由事物的表面现象经验性地得到一些结论，这停留在抽象的第一个阶段.而原理性抽象把握的是事物的因果性和规律性的联系.在数学的学习中，往往需要联系事物之间的关系，为数学的高度抽象关系，建构起更加具体形象的认知.章建跃认为，人类的智慧表现在用简单的概念阐明科学的基本问题，用相似的方法解决不同的问题，而数学的方法就是这样的方法.在数学中，自然数不仅打开了数学研究的大门，也为数学推理验证由“有......
2023-08-17
-
高中数学核心素养与认知事物关联的价值详细阅读
发展数学素养是时代的需要，聚焦数学核心素养是数学课程改革的趋势.我们所处的是一个大数据时代，数字化程度高，信息交流广泛，而数学正直接或间接地渗透到社会生活的各个领域，广泛地影响着人们的生活.数学运算是用数学的方法分析事物之间的关系，用符号、字母表示事物的形态，用数据、图标、关系式表示事物之间的联系，通过事物之间的联系探寻解决问题的运算思路，制定运算法则准确计算所产生的结果，这都体现着数学运算对认知......
2023-08-17
-
高中数学核心素养-考查直观想象能力详细阅读
直观想象在数学核心素养体系中具有重要的地位，与其他数学学科核心素养密不可分.在复杂情境中发现问题、解决问题，通常需要先通过直观想象对问题进行分析、探寻问题实质，再通过数学抽象、数学建模将其转化为数学问题.在复杂的逻辑推理或数学运算中，也需要运用直观想象来理清思路、简化运算；在大数据分析时，有时也要借助图表使数据更加直观.【案例4-14】把数学问题直观化、图形化问题：在平面四边形ABCD中，∠ADC......
2023-08-17
-
高中数学核心素养：直观想象能力的思维品质研究详细阅读
直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.【案例4-13】利用几何直观形成论证思路问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.图4-29分......
2023-08-17
-
高中数学：直观想象素养的渗透详细阅读
《普通高中数学课程标准（2017年版）》对培养学生直观想象素养的要求体现在多个方面.比如，在必修课程与选择性必修课程中，突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联，加强对数学整体性的理解.必修课程如图4-11所示，选择性必修课程如图4-12所示.图4-12在必修课程中，从函数观点看一元二次方程和一元一次不等式的教学，让学生逐渐养成借助直观理解概念的习惯.在三角函数......
2023-08-17
-
高中数学核心素养：直观想象素养的历史脉络详细阅读
【案例4-1】筹算春秋末年，人们已经普遍掌握了完备的十进制记数法，使用了筹算这种先进的计算方法，谙熟九九乘法表、整数四则运算，并能使用分数.所谓筹算，是以可有数字的竹筹（即算筹）来计算数目.在《汉书·律历志》中有算筹形状与大小的记载：“其算法用竹，径一分，长六寸，二百七十一枚而成六觚（gu），为一握.”算筹记数规则最早载于《孙子算经》：“凡算之法，先识其位.一纵十横，百立千僵.千十相望，万百相当.......
2023-08-17
-
高中数学核心素养：直观想象力的定义及范围详细阅读
和抽象一样，直观想象是认识事物的基本方式.和抽象不同，直观想象简单、直接（付诸感官），容易掌握和使用.而且，直观想象是进一步抽象的必要基础.作为直观与想象的重要结果，图形是数学研究的基本对象之一（另一个是数字，包括用字母表示的数字），图形表示则是数学研究的一个重要方法（尤其是在非几何领域，对非图形问题）.在数学教学中，利用图形可以更简单、直接地刻画和描述问题，探索和形成思路，寻找和发现结论，记忆和......
2023-08-17
相关推荐