直观想象从思维角度看，就是通过建构数学问题的直观模型，在观察、分析直观模型的基础上，对事物的空间形式，特别是图形进行进一步的想象，把握其位置关系、形态变化与运动规律.【案例4-13】利用几何直观形成论证思路问题1：设函数f（x）的定义域为R，满足f（x+1）=2f（x），且当x∈（0，1]时，f（x）=x（x-1）.若对任意x∈（-∞，m]，都有，则m的取值范围是__________.图4-29分......
2023-08-17
高中数学核心素养：培养思维，直观想象价值
【摘要】：问题6：怎样用棱数E和面数F表示多面体所有多边形的内角和？在假设多面体的F个面分别是n1，n2，n3，…图4-7中所有多边形的内角和是.图4-7案例4-4中，采用降维思想和转化策略将空间问题转化为平面问题来研究，这种处理问题的方法是立体几何中的重要思想方法，在降维和升维（如翻折）过程中关健要弄清不变量与变量.从案例4-4中可以看到，转化策略是解决数学问题的主要方法之一，如何转化是关健.
在数学研究的探索中，通过直观手段的运用以及借助直观展开想象，从而发现结论、做出猜想的例子比比皆是.数学思维不是仅仅在抽象层面展开，而是在很多场合中借助直观手段展开的.所以，直观想象在数学活动中“是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础”.
【案例4-4】多面体欧拉公式的发现
问题1：如图4-5所示为6个多面体，分别数出它们的顶点数V、面数F和棱数E，填入表4-1.
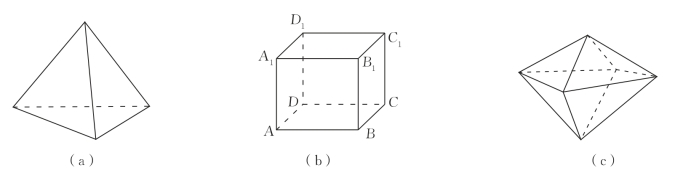
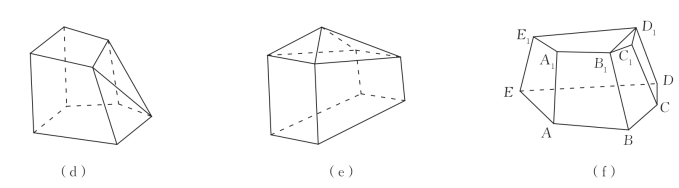
图4-5
表4-1
观察表4-1中各组数据，猜想V、F、E之间的规律：____________________.并思考是否任意一个多面体都有上述规律.
（问题1旨在让学生在解决问题的过程中去观察、猜想、探索，培养和锻炼学生的探究能力.）
问题2：图4-6所示为3个多面体，分别数出它们的顶点数V、面数F和棱数E，填入表4-2.
图4-6
表4-2
（问题2旨在用简单直观的问题情景激发学生探索兴趣）
问题3：比较前面问题1和问题2中的图形，如果这些多面体的表面都是用橡皮膜制成的，并且可以向它们的内部充气，那么其中哪些多面体能够连续变形（不破裂、不粘连），最后其表面可变为一个球面？哪些能变为一个环面？哪些可变为两个对接球面？
（问题3旨在引导学生通过收集数据，观察数据，处理数据，直观想象，提出假设.）
引入“简单多面体”的概念：假设多面体的表面是橡皮膜制成的，可以向它们的内部充气，那么能够连续变形（不破裂、不粘连），表面能变为一个球面的多面体，叫做简单多面体.
猜想：观察表中各组数据，对于简单多面体，V、F、E之间的关系是________.
引入欧拉（L.Euler）公式：（拓展阅读）著名数学家、物理学家和天文学家欧拉（Léonard Euler），生于瑞士巴塞尔，1720年进入巴塞尔大学学习神学和希伯来语，因数学才能突出受到约翰·贝努利的赏识与特别指导，曾获得硕士学位.1727年应邀到俄国讲学.1733年任彼得堡科学院数学教授.1741年移居柏林，任柏林科学院物理数学所所长.1766年再次到俄国.1783年卒于彼得堡.
欧拉19岁开始发表论文，半个多世纪里始终以充沛的精力，不倦地工作.他28岁时右眼失明，59岁后左眼也视力减退，渐至失明.在失明的十多年里，欧拉以惊人的毅力，凭着记忆和心算，仍然坚持富有成果的研究，直到生命的最后一刻.欧拉的工作涉及数学的各个领域，他是历史上最多产的数学家之一，后人计划出版他的全集多达72卷.
欧拉是变分法的奠基人和研究复变函数的先驱者，对牛顿、莱布尼茨的微积分学和傅立叶级数的发展起了相当大的推动作用.
问题4：任意一个简单多面体，假设它们的表面是橡皮膜制成的，将它们压缩到其底面所在的平面，如何画出压缩后的平面图形？
问题5：在压缩前后哪些量发生了变化，而哪些量没有发生变化？（问题4和问题5旨在通过课件强化学生多种感官对数学问题的感知.）
问题6：怎样用棱数E和面数F表示多面体所有多边形的内角和？
（1）在假设多面体的F个面分别是n1，n2，n3，…，nF边形，则各个面的内角和是_______________.
（2）其中n1+n2+n3+…+nF和多面体的棱数E的关系为_____________________.
所以多面体的各个面的内角和是____________________.
问题7：怎样用顶点数V表示平面图形中所有多边形的内角和？
图4-7（b）中所有多边形的内角和是.
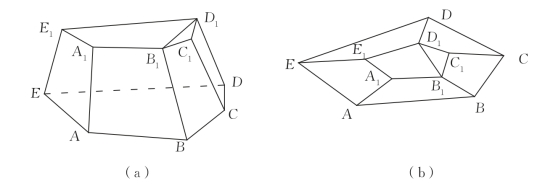
图4-7
（问题7旨在通过引导学生回忆证明过程，来体会所用到的数学思想方法.）
案例4-4中，采用降维思想和转化策略将空间问题转化为平面问题来研究，这种处理问题的方法是立体几何中的重要思想方法，在降维和升维（如翻折）过程中关健要弄清不变量与变量.从案例4-4中可以看到，转化策略是解决数学问题的主要方法之一，如何转化是关健.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：直观想象的认知关联价值详细阅读
提升学生直观想象核心素养，在帮助他们认知事物之间的关联方面具有非同一般的价值.通过直观想象素养的培养，帮助学生通过数学间的内在联系，将数学问题图像化，分析问题的本质关联，从而将问题理解得更为深入，问题的解决得以顺利进行.三角函数的周期性1.问题的提出“离离原上草，一岁一枯荣，野火烧不尽，春风吹又生”蕴含了什么数学知识？......
2023-08-17
-
高中数学核心素养-考查直观想象能力详细阅读
直观想象在数学核心素养体系中具有重要的地位，与其他数学学科核心素养密不可分.在复杂情境中发现问题、解决问题，通常需要先通过直观想象对问题进行分析、探寻问题实质，再通过数学抽象、数学建模将其转化为数学问题.在复杂的逻辑推理或数学运算中，也需要运用直观想象来理清思路、简化运算；在大数据分析时，有时也要借助图表使数据更加直观.【案例4-14】把数学问题直观化、图形化问题：在平面四边形ABCD中，∠ADC......
2023-08-17
-
高中数学核心素养：推理培养思维，具有重要价值详细阅读
逻辑思维有两个方面：①得到数学结论、构建数学体系的重要方式；②数学严谨性的基本保证.逻辑思维是人们在数学活动中进行交流的基本思想保证.《普通高中数学课程标准（2017年版）》中明确指出“通过高中数学课程的学习，学生能掌握逻辑推理的形式，学会有逻辑地思考问题.”数学知识大部分都是程序性知识，在经历了知识的陈述性阶段学习后，需要通过意识控制的练习达到熟练程度，从而过渡到自动化阶段.概念的简单描述，帮助......
2023-08-17
-
高中数学核心素养的思维价值详细阅读
对学生来说，数学首先是利用自己的生活经验对数学现象的一种“解读”，这需要的是由数学向学生日常生活的“回归”.但是到了更高阶段的抽象时，已经没有必要每次的运算或者推导都要回归到具体事物间的关系上去.又或者说，除了“解读”外，我们还需要帮助学生由“日常数学”上升到“学校数学”.这其中，蕴含着数学抽象的两个阶段.在数学的学习中，学生一般通过理解抽象性概念，练习公式以及变式，在数学应用中创建抽象化的产物，......
2023-08-17
-
高中数学核心素养：直观想象素养的历史脉络详细阅读
【案例4-1】筹算春秋末年，人们已经普遍掌握了完备的十进制记数法，使用了筹算这种先进的计算方法，谙熟九九乘法表、整数四则运算，并能使用分数.所谓筹算，是以可有数字的竹筹（即算筹）来计算数目.在《汉书·律历志》中有算筹形状与大小的记载：“其算法用竹，径一分，长六寸，二百七十一枚而成六觚（gu），为一握.”算筹记数规则最早载于《孙子算经》：“凡算之法，先识其位.一纵十横，百立千僵.千十相望，万百相当.......
2023-08-17
-
高中数学：直观想象素养的渗透详细阅读
《普通高中数学课程标准（2017年版）》对培养学生直观想象素养的要求体现在多个方面.比如，在必修课程与选择性必修课程中，突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联，加强对数学整体性的理解.必修课程如图4-11所示，选择性必修课程如图4-12所示.图4-12在必修课程中，从函数观点看一元二次方程和一元一次不等式的教学，让学生逐渐养成借助直观理解概念的习惯.在三角函数......
2023-08-17
-
高中数学核心素养：直观想象力的定义及范围详细阅读
和抽象一样，直观想象是认识事物的基本方式.和抽象不同，直观想象简单、直接（付诸感官），容易掌握和使用.而且，直观想象是进一步抽象的必要基础.作为直观与想象的重要结果，图形是数学研究的基本对象之一（另一个是数字，包括用字母表示的数字），图形表示则是数学研究的一个重要方法（尤其是在非几何领域，对非图形问题）.在数学教学中，利用图形可以更简单、直接地刻画和描述问题，探索和形成思路，寻找和发现结论，记忆和......
2023-08-17
相关推荐