某学生回答：“是的.”并给出证明如下：假设当n=k时，等式成立，即2+4+6+……+2k+2（k+1）=k2+k+2+2（k+1），而k2+2k+1+k+1+2=（k+1）2+（k+1）+2，等式也成立.你认为这个学生回答的对吗？......
2023-08-17
数学核心素养评估：逻辑推理能力
【摘要】：逻辑推理素养作为高中数学学科核心素养之一，从培养和发展学生关键能力的角度出发，也是其考查标准的重要维度之一.【案例3-20】数形结合问题：若实系数一元二次方程x2+ax+2b=0有两个根，一个根在区间（0，1）内，另一个根在区间（1，2）内，求：（1）点（a，b）对应的区域的面积；（2）的取值范围；（3）（a-1）2+（b-2）2的值域.解 可将看作点（a，b）和（1，2）连线的斜率，（a-1）2
逻辑推理素养作为高中数学学科核心素养之一，从培养和发展学生关键能力的角度出发，也是其考查标准的重要维度之一.
【案例3-20】数形结合
问题：若实系数一元二次方程x2+ax+2b=0有两个根，一个根在区间（0，1）内，另一个根在区间（1，2）内，求：（1）点（a，b）对应的区域的面积；（2）
的取值范围；（3）（a-1）2+（b-2）2的值域.
解 可将
看作点（a，b）和（1，2）连线的斜率，（a-1）2+（b-2）2则表示点（a，b）与定点（1，2）之间的距离的平方.
方程x2+ax+2b=0的两根在区间（0，1）和（1，2）上的几何意义分别是：函数y=f（x）=x2+ax+2b与x轴的两个交点的横坐标分别在区间（0，1）和（1，2）内，且x1x2=2b＞0，
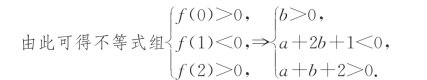
∴在如图3-14所示的aOb坐标平面内，满足约束条件的点（a，b）对应的平面区域为△ABC（不包括边界）.
图3-14
（3）∵（a-1）2+（b-2）2表示区域内的点（a，b）与定点（1，2）之间距离的平方，由图3-14可知，当取点C（-1，0）时有最小值8，当取点A（-3，1）时有最大值17，∴（a-1）2+（b-2）2的值域为（8，17）.
案例3_20在学生逻辑推理的基础上，将问题合情转化，借助几何手段对代数问题进行研究，充分考查了学生运用数形结合的能力.
有关高中数学核心素养的文章
- 详细阅读
-
培养创造能力：高中数学核心素养详细阅读
探究7：若将焦点F改为点F2，对应准线改为直线=1，则圆、椭圆是否具有组合1、2、3的性质？事实上，点F2是直线l的极点，直线l是点F2的极线.给定圆或圆锥曲线Γ，当极点在Γ内时，其对应的极线与Γ相离；当极点在Γ上时，其对应的极线与Γ相切；当极点在Γ外时，其对应的极线与Γ相交.由极点和对应的极线，可得一系列的调和点列.......
2023-08-17
-
高中数学核心素养：逻辑推理渗透数学学习详细阅读
逻辑推理素养作为高中数学六大核心素养之一，承载着落实数学学科严谨性特征的重要责任.在每一个数学学习的环节中，都可以将逻辑推理素养进行合理渗透，从而提高学生的逻辑推理能力.数列的最值初步研究1.预习演练问题反思 ①类比函数的最值，如何定义数列的最值？问题：设等差数列｛an｝的前n项和为Sn，已知a1＜0，S8=S13，则当n取何值时，Sn最小？......
2023-08-17
-
高中数学核心素养-考查直观想象能力详细阅读
直观想象在数学核心素养体系中具有重要的地位，与其他数学学科核心素养密不可分.在复杂情境中发现问题、解决问题，通常需要先通过直观想象对问题进行分析、探寻问题实质，再通过数学抽象、数学建模将其转化为数学问题.在复杂的逻辑推理或数学运算中，也需要运用直观想象来理清思路、简化运算；在大数据分析时，有时也要借助图表使数据更加直观.【案例4-14】把数学问题直观化、图形化问题：在平面四边形ABCD中，∠ADC......
2023-08-17
- 详细阅读
-
高中数学核心素养-逻辑推理在数学学科中的价值详细阅读
逻辑推理的数学学科价值体现在两方面：①逻辑推理是得到数学结论，构建数学体系的重要方式；②逻辑推理是数学严谨性的基本保证.在数学结论的获得、数学体系的构建方面，逻辑推理是重要的、不可或缺的方式.在高中数学学习过程中，逻辑推理渗透到了每个学习内容板块和学习环节中.严谨性是数学学科的重要特征之一，而逻辑推理为这一特点的形成提供了重要的保证.直线的方程概念引入问题1：在直角坐标系中，如何确定一条直线？......
2023-08-17
-
高中数学核心素养：图形计算器辅助提升数学抽象详细阅读
20世纪90年代，美国德州仪器（Texas Instruments，TI）等专业技术生产企业开始逐渐扩大市场规模，带着不同类型的图形计算器产品叩开了中国学校的大门.图形计算器是一款集数据处理、方程解析、图表绘制、模型建立等多种功能于一身的新型手持学习工具，为数理化等学科的课堂教学带来了深刻的变化.2010年，TI依靠强大的技术团队，成功构建了TI-Nsipre图形计算器和无线数学实验室，帮助很多学......
2023-08-17
-
高中数学核心素养详解详细阅读
通过图形的表征与变换，理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化，都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.【案例4-15】构造几何模型，破解思维瓶颈问题：设点P是函数的图像上的任意一点，点Q（2a，a-3），（a∈R），则|PQ|的最小值为__________.解：函数的图像是以C（1，0）为圆心，半径等于2的圆在x轴以下的半圆，含点（-1，0）、（3，0）.......
2023-08-17
相关推荐