逻辑推理素养作为高中数学六大核心素养之一，承载着落实数学学科严谨性特征的重要责任.在每一个数学学习的环节中，都可以将逻辑推理素养进行合理渗透，从而提高学生的逻辑推理能力.数列的最值初步研究1.预习演练问题反思 ①类比函数的最值，如何定义数列的最值？问题：设等差数列｛an｝的前n项和为Sn，已知a1＜0，S8=S13，则当n取何值时，Sn最小？......
2023-08-17
高中数学学习：提高逻辑推理能力
【摘要】：高中数学学科六大核心素养都是数学学科育人价值的集中体现，其中逻辑推理素养尤其在数学学科严谨性特征上有独特价值.提升学生的逻辑推理素养，对提高学生的思维品质有积极意义.在数学学科考查逻辑推理素养的方面，考查思维品质是一个重要纬度.表3-1为《普通高中数学课程标准（2017年版）》中对于逻辑推理素养的水平划分.表3-1【案例3-18】解析几何推广和平面解析几何的观点相同，在空间中，空间平面和曲面可以看
高中数学学科六大核心素养都是数学学科育人价值的集中体现，其中逻辑推理素养尤其在数学学科严谨性特征上有独特价值.提升学生的逻辑推理素养，对提高学生的思维品质有积极意义.在数学学科考查逻辑推理素养的方面，考查思维品质是一个重要纬度.
表3-1为《普通高中数学课程标准（2017年版）》中对于逻辑推理素养的水平划分.
表3-1
【案例3-18】解析几何推广
和平面解析几何的观点相同，在空间中，空间平面和曲面可以看作是适合某种条件的动点的轨迹，在空间直角坐标系O-xyz中，空间平面和曲面的方程是一个三元方程F（x，y，z）=0.
（1）类比平面解析几何中直线的方程，写出①过点P（x0，y0，z0），法向量为n→=（A，B，C）的平面的点法式方程；②平面的一般方程；③在x、y、z轴上的截距分别为a、b、c的平面的截距式方程（不需要证明）.
（2）设F1、F2为空间中的两个定点，|F1F2|=2c，我们将曲面Γ定义为满足|PF1|+|PF2|=2a（a＞c）的动点P的轨迹，试建立一个适当的空间直角坐标系O-xyz，求曲面Γ的方程.
（3）对（2）中的曲面Γ，指出和证明曲面Γ的对称性，并画出曲面Γ的直观图.
（2）以两个定点F1、F2的中点为坐标原点O，以F1，F2所在的直线为y轴，以线段F1F2的垂直平分线为x轴，以与xOy平面垂直的直线为z轴，建立空间直角坐标系O-xyz.
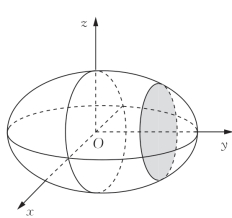
图3-13 曲面Γ的直观图
（3）由于点（x，y，z）关于坐标原点O的对称点（-x，-y，-z）也满足①式，说明曲面Γ关于坐标原点O对称；由于点（x，y，z）关于x轴的对称点（x，-y，-z）也满足①式，说明曲面Γ关于x轴对称；同理，曲面Γ关于y轴对称；关于z轴对称.由于点（x，y，z）关于xOy平面的对称点（x，y，-z）也满足①式，说明曲面Γ关于xOy平面对称；同理，曲面Γ关于xOz平面对称；关于yOz平面对称.
由以上的讨论，可得曲面Γ的直观图，如图3-13所示.
案例3-18充分考查了学生在已有知识学习的基础上，将研究方法进行迁移的能力，更考查了学生在合情逻辑推理的前提下，开展新知识学习的能力.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心能力提升详细阅读
《普通高中数学课程标准2017年版》提出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必须的数学基础知识、基本技能、基本思想、基本活动经验；提高从数学角度发现和提出问题的能力、分析和解决问题的能力.从关键能力角度考察数学运算素养，可以从运算的本质出发，考察数学运算对象，理解数学运算的应用，类比运算法则的运用等.【案例2-17】极限思想中的数学运算素养1.真题重现2.考点分析利用极限的......
2023-08-17
-
高中数学核心素养之逻辑推理攻略详细阅读
某学生回答：“是的.”并给出证明如下：假设当n=k时，等式成立，即2+4+6+……+2k+2（k+1）=k2+k+2+2（k+1），而k2+2k+1+k+1+2=（k+1）2+（k+1）+2，等式也成立.你认为这个学生回答的对吗？......
2023-08-17
-
数学核心素养评估：逻辑推理能力详细阅读
逻辑推理素养作为高中数学学科核心素养之一，从培养和发展学生关键能力的角度出发，也是其考查标准的重要维度之一.【案例3-20】数形结合问题：若实系数一元二次方程x2+ax+2b=0有两个根，一个根在区间（0，1）内，另一个根在区间（1，2）内，求：（1）点（a，b）对应的区域的面积；（2）的取值范围；（3）（a-1）2+（b-2）2的值域.解 可将看作点（a，b）和（1，2）连线的斜率，（a-1）2......
2023-08-17
-
提高高中数学核心素养详细阅读
数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的思维品质与关键能力，是数学课程目标的集中体现.它是在数学学习的过程中逐步形成的.数学核心素养包括：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析.这些数学核心素养既有独立性，又相互交融，形成一个有机整体.核心素养下的数学新高考怎么考？......
2023-08-17
-
培养创造能力：高中数学核心素养详细阅读
探究7：若将焦点F改为点F2，对应准线改为直线=1，则圆、椭圆是否具有组合1、2、3的性质？事实上，点F2是直线l的极点，直线l是点F2的极线.给定圆或圆锥曲线Γ，当极点在Γ内时，其对应的极线与Γ相离；当极点在Γ上时，其对应的极线与Γ相切；当极点在Γ外时，其对应的极线与Γ相交.由极点和对应的极线，可得一系列的调和点列.......
2023-08-17
- 详细阅读
- 详细阅读
相关推荐