苏联教育家马卡连柯曾说过：“游戏在儿童生活中具有重要的意义，具有与成人活动、工作和劳动同样重要的意义.”游戏本身具有愉快、自由及探索的特性，游戏是孩子们的天性，也是认识世界的途径之一，其不但可以满足学生的好奇心理，还能有效培养他们各方面的能力.如今数学建模的教学课堂普遍枯燥乏味，而简单的数学游戏能够通过创设一个游戏化的场景让学生更加放松，从而让学生对于传统教学模式不那么排斥，可以更有效地理解数学概......
2023-08-17
简单数学游戏提升高中逻辑推理素养
【摘要】：图3-11分层目标 ：第一层，是否能找到一个规律来描述兔子的数量变化.第二层，是否能尝试利用流程图来设计一个推算某个月兔子数量的算法.第三层，是否能在课后尝试计算兔子的数量与月之间的关系.解 斐波纳契数列：1，1，2，3，5，8，13,21,34,55,89,144,…
数学史上一系列经典例题的引入、求解和推广，不仅可以提高学生学习兴趣，使学生明确逻辑推理在学习数学时的重要性，还能够让学生学会将学习所获应用到实际经典问题的研究中，从而提升其逻辑推理能力.现代教育技术可以将逻辑推理的思想与计算机算法进行结合，让历史与现代科技亲密接触.
【案例3-16】斐波纳契数列
问题：第一个月有一对刚诞生的兔子，第二个月之后它们可以生育，每月每对可生育的兔子会诞下一对新兔子，假设兔子都不会死去，问一年之后共有多少对兔子？
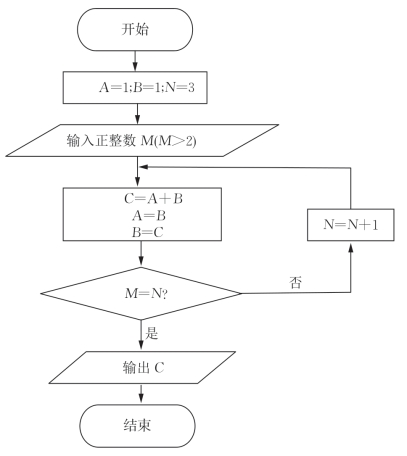
图3-11
分层目标 （可以让学生根据自己的能力以及实际情况选择层次）：
（1）第一层，是否能找到一个规律来描述兔子的数量变化.
（2）第二层，是否能尝试利用流程图来设计一个推算某个月兔子数量的算法.
（3）第三层，是否能在课后尝试计算兔子的数量与月之间的关系.
解 斐波纳契数列：1，1，2，3，5，8，
13,21,34,55,89,144,…
可知一年之后有144对兔子.
用an表示第n个月兔子的数量，则数列{an}满足a1=1，a2=1，an=an-1+an-2（n∈N*，n＞2）.
通项公式为（学生课后拓展作业）an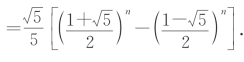
算法程序框图如图3-11所示.
案例3-16旨在让学生充分体会递推思想，同时弥补教材上对斐波纳契数列介绍的不足.斐波纳契数列充分体现了递推思想的特点，是用来加深学生对递推思想理解的好例子，并且在数列的发展史上有着重要的意义，对现实生活中的许多问题也有重要的指导作用.目前教材仅将其作为课外的英语教材，使用不少学生在无意中错过了如此美妙精彩的东西.
递推的思想在算法中也有重要价值，许多循环语句的设计都要利用到递推的思想.将斐波纳契数列引入递推思想的教学中，既能用历史经典问题有效反应递推思想，又能将这个重要思想深入到现代科技中，做到以递推思想为媒介，将数学史与现代技术完美结合.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：简单数学游戏辅助直观想象提详细阅读
人们对数学有一个严重的误解，认为它只是枯燥无味的计算.这种观点完全是错误的，事实上，数学是关于想象力、洞察力和直觉的学科，真正的数学灵感正是来自这三者.数学是抽象游戏的集合，是科学，也是一种看待事物的角度.在这个抽象规则构成的数学游戏小世界里，有精彩的解题思路、巧妙的解题技巧、标准的序列、有力的方法、熟悉的布阵、致胜的奇招和杰出的组合等.【案例4-11】用复数找宝虚数闯进数学领地之后，足足有几个世......
2023-08-17
-
提升高中数学核心素养详细阅读
美国的科普学家马丁·加德纳（Martin Gardner）认为，在数学教育的过程中要想避免那些没有价值并且枯燥的东西，老师就需要给学生提供一些有趣的智力题或是游戏性的教学，另外也可以提供一些比较搞笑的笑话或是悖论，这些都可以调动学生学习的积极性，唤醒学生的学习欲望.这样就肯定了数学游戏在高中数学教学中的作用.数学知识的抽象性和逻辑性决定了数学课堂的枯燥和无味，但随着素质教育的不断推进，数学课堂也在......
2023-08-17
-
高中数学核心素养之逻辑推理攻略详细阅读
某学生回答：“是的.”并给出证明如下：假设当n=k时，等式成立，即2+4+6+……+2k+2（k+1）=k2+k+2+2（k+1），而k2+2k+1+k+1+2=（k+1）2+（k+1）+2，等式也成立.你认为这个学生回答的对吗？......
2023-08-17
-
高中数学核心素养：逻辑推理渗透数学学习详细阅读
逻辑推理素养作为高中数学六大核心素养之一，承载着落实数学学科严谨性特征的重要责任.在每一个数学学习的环节中，都可以将逻辑推理素养进行合理渗透，从而提高学生的逻辑推理能力.数列的最值初步研究1.预习演练问题反思 ①类比函数的最值，如何定义数列的最值？问题：设等差数列｛an｝的前n项和为Sn，已知a1＜0，S8=S13，则当n取何值时，Sn最小？......
2023-08-17
-
高中数学核心素养-逻辑推理在数学学科中的价值详细阅读
逻辑推理的数学学科价值体现在两方面：①逻辑推理是得到数学结论，构建数学体系的重要方式；②逻辑推理是数学严谨性的基本保证.在数学结论的获得、数学体系的构建方面，逻辑推理是重要的、不可或缺的方式.在高中数学学习过程中，逻辑推理渗透到了每个学习内容板块和学习环节中.严谨性是数学学科的重要特征之一，而逻辑推理为这一特点的形成提供了重要的保证.直线的方程概念引入问题1：在直角坐标系中，如何确定一条直线？......
2023-08-17
- 详细阅读
-
高中数学核心素养：图形计算器辅助提升数学抽象详细阅读
20世纪90年代，美国德州仪器（Texas Instruments，TI）等专业技术生产企业开始逐渐扩大市场规模，带着不同类型的图形计算器产品叩开了中国学校的大门.图形计算器是一款集数据处理、方程解析、图表绘制、模型建立等多种功能于一身的新型手持学习工具，为数理化等学科的课堂教学带来了深刻的变化.2010年，TI依靠强大的技术团队，成功构建了TI-Nsipre图形计算器和无线数学实验室，帮助很多学......
2023-08-17
相关推荐