高中数学核心素养：图形计算器辅助推理技巧提升

2023-08-17 理论教育版权反馈

【摘要】：图形计算器作为研究数学问题的一个工具，能够在学生开展数学学习的过程中提供过一定的辅助作用.尤其是它在作函数图像上的操作简便性，为学生从众多特殊情况中归纳和抽象出问题本质，并在此基础上进行演绎证明，提供了很好的帮助.【案例3-15】借助函数图像研究函数性质问题1：函数y=loga x的相关性质.如图3-3所示，利用动态图展示函数图像，能够明确当底数a取不同值时，函数单调性的变化，也能够明确无论底数如

图形计算器作为研究数学问题的一个工具，能够在学生开展数学学习的过程中提供过一定的辅助作用.尤其是它在作函数图像上的操作简便性，为学生从众多特殊情况中归纳和抽象出问题本质，并在此基础上进行演绎证明，提供了很好的帮助.

【案例3-15】借助函数图像研究函数性质

问题1：函数y=loga x的相关性质.

如图3-3所示，利用动态图展示函数图像，能够明确当底数a取不同值时，函数单调性的变化，也能够明确无论底数如何变化，函数的定义域不变，且过定点.

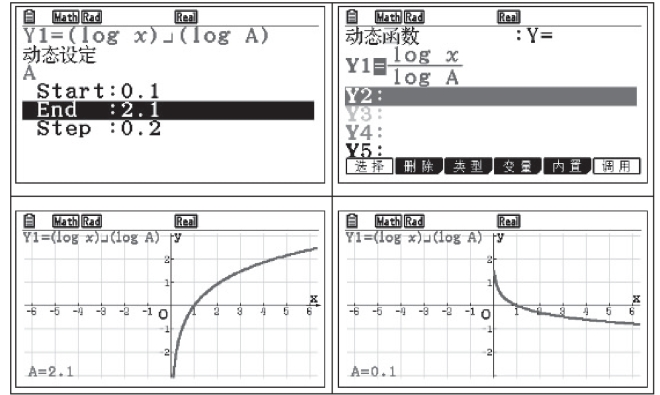
pagenumber_ebook=88,pagenumber_book=79

图3-3

问题2：研究函数y=logax与y=ax的关系.

通过图3-4所示动态观察函数图像关于直线y=x对称，观察函数与其反函数在图像上的关系，明确两个函数的内在本质联系.

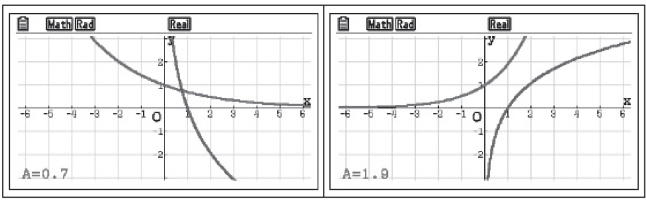
pagenumber_ebook=88,pagenumber_book=79

图3-4

问题3：研究函数y=loga x与y=loga（-x）、y=-loga x、y=-loga（-x）的关系.

经过观察可得函数y=loga x与y=loga（-x）的图像关于y轴对称，如图3-5所示.

pagenumber_ebook=89,pagenumber_book=80

图3-5

借助类似的活动，学生通过输入动态图，可以直观分析得到以下结论：

函数y=logax与y=-logax的图像关于x轴对称，如图3-6所示；函数y=logax与y=-loga（-x）图像关于原点中心对称，如图3-7所示.

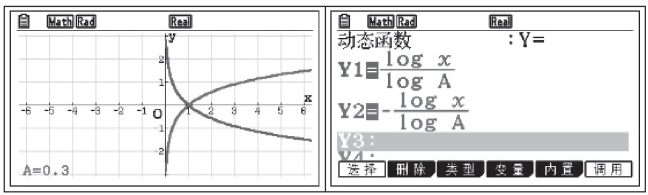
pagenumber_ebook=89,pagenumber_book=80

图3-6

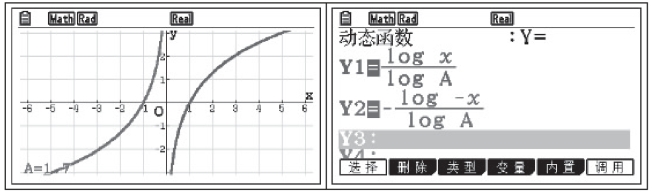
pagenumber_ebook=89,pagenumber_book=80

图3-7

问题3当中的3个活动，是以对函数图像的变化为载体，通过直观地观察得到相应的函数图像的变化特点.图像的变换研究是问题的表象，建议在活动开展的时候，将函数图像的变换归结到函数图像上的每个点坐标的变换，从而更加直观和清晰地明确函数图像变换的本质，并且把归纳得到的性质一般化，推广到y=f（x）与y=f（-x）、y=-f（x）、y=-f（-x）的函数图像之间的关系.

由于本问题中的函数图像可能出现部分重合的现象，建议采用图形功能，通过适当调整线型来帮助观察函数图像的变换.

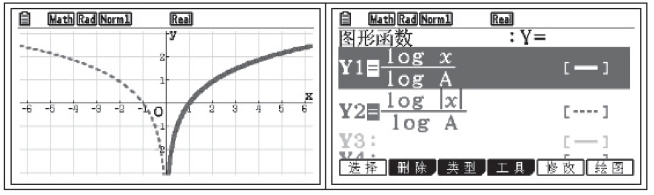
pagenumber_ebook=90,pagenumber_book=81

图3-8

通过观察函数图像，可以发现当x＞0时，函数图像与y=loga x重合，当x＜0时，图像与x＞0部分的函数图像关于y轴对称，如图3-8所示.这与函数是偶函数的性质一致.

通过观察函数的图像可以发现，函数y=logax的图像在x轴上方的部分被保留了，而在x轴下方的部分以x轴为对称轴向上翻折，得到了函数的图像，如图3-9所示.

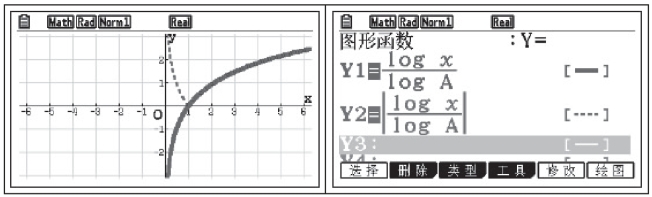
pagenumber_ebook=90,pagenumber_book=81

图3-9

通过观察函数图像，并结合上两个活动的结果分析，可以直观地观察到函数是由函数y=loga x经过多次翻折得到的，如图3-10所示.

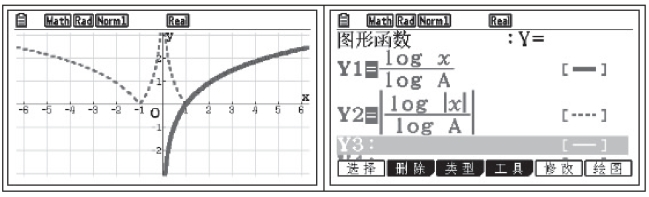
pagenumber_ebook=90,pagenumber_book=81

图3-10

问题4中的3个活动都是从函数图像的变换角度出发，研究解析式中的绝对值对于函数图像产生的影响.在活动开展的过程当中，可以从图像观察入手，经过分析后得出规律.为了帮助学生深入理解问题，在研究图像变换的表象之后，建议对这些变换为什么会发生进行研究.绝对值对于函数图像的影响并非对数函数独有，活动之所以采用对数函数图像作为载体，其原因在于对数函数图像形状相对简单，能够更加清晰直观地看出函数图像的变换，便于总结合归纳性质.在研究对数函数图像的基础上，可将问题推广到函数y=f（x）与函数之间的关系.

从案例3_15中可以看出，随着信息技术的发展，数学学科中的逻辑推理可以将信息技术的直观展示等内容作为逻辑推理的辅助手段.数学学科中的逻辑推理可以基于观察的前提进行归纳，并在此基础上对归纳的结果进行严格的演绎证明.信息技术正是为我们提供了多渠道多方面直观展示问题的平台和媒介，为学生进行归纳提供了基础和帮助.

高中数学核心素养：图形计算器辅助推理技巧提升

相关推荐