对于学科来说，抽象是数学的首要特征，抽象为推理提供了对象，为模型提供了依据，为数学的广泛应用提供了基础.两种事物，如果有相同的量或形，便可用相同的数学方法，因而数学必然、也必须是抽象的.对于育人来讲，“数学虽不研究事物的质，但任一事物必有量和形，所以数学是无处不在、无时不用的”.因而学生经历数学的抽象，不仅由此生成了数学的研究内容，更具普遍意义的是抽象的过程，能让学生学习如何从量或形的视角去观察、......
2023-08-17
高中数学核心素养-逻辑推理在数学学科中的价值
【摘要】：逻辑推理的数学学科价值体现在两方面：①逻辑推理是得到数学结论，构建数学体系的重要方式；②逻辑推理是数学严谨性的基本保证.在数学结论的获得、数学体系的构建方面，逻辑推理是重要的、不可或缺的方式.在高中数学学习过程中，逻辑推理渗透到了每个学习内容板块和学习环节中.严谨性是数学学科的重要特征之一，而逻辑推理为这一特点的形成提供了重要的保证.直线的方程概念引入问题1：在直角坐标系中，如何确定一条直线？
逻辑推理的数学学科价值体现在两方面：①逻辑推理是得到数学结论，构建数学体系的重要方式；②逻辑推理是数学严谨性的基本保证.
在数学结论的获得、数学体系的构建方面，逻辑推理是重要的、不可或缺的方式.在高中数学学习过程中，逻辑推理渗透到了每个学习内容板块和学习环节中.严谨性是数学学科的重要特征之一，而逻辑推理为这一特点的形成提供了重要的保证.
【案例3-6】直线的方程概念引入
问题1：在直角坐标系中，如何确定一条直线？以经过点A的直线为例，如图3-2所示，只确定经过点A，但方向不定的直线有无数条，如果给定一个方向
，则可以确定唯一的直线l.把像
这样平行于直线l的向量称为直线l的一个方向向量.
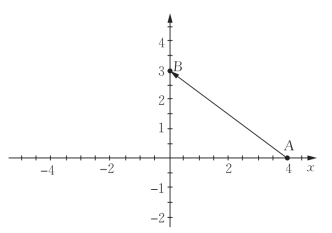
图3-2
所以已知直线上的一个点、一个方向向量，可以在坐标平面内确定一条直线.
注：（1）如果有学生提到两点可以确定一条直线，可指出其想法正确，除给定点A点以外，确定另一个点，如B（0，3），恰恰为直线l提供了方向，可以通过点A、B确定直线l的一个方向向量
=（-4，3）.
（2）如果有学生提到确定倾斜角，可指出倾斜角为直线提供了一个方向，在确定一个点和一个方向的情况下，可以在坐标平面内确定直线l，可以用向量来刻画直线的方向，引出方向向量的概念.
追问2：两点确定一条直线完全正确，但如何证明一次函数的图像就是直线？
答：一次函数的解析式也可看作一个一元二次方程，如果用一次函数进行验证就变成了“方程的解满足方程”了，与直线l无关.
（3）（极端状况）毫无反应，继续引导：通过一个点A和一个方向向量
确定直线l，不妨从点C与点A和
的联系角度进行研究（必要时给出图示）.
归纳方法：通过向量平行来证明A、B、C三点共线，从而证明点C在直线l上.
注：由于问题是求直线l的方程，不排除个别学生可能还是会出现只写了第一部分的情况，如果出现这种情况，可以实物投影后请学生指出错误的地方，并再度强调直线的方程概念的两方面缺一不可，根据当时情况决定是否需要再把A⊆B且B⊆A拿出来对概念进行强调.
当u≠0且v≠0时，上述方程可化为
，称为直线的点方向式方程.
问题5：（习题）已知直线l过点P（0，2），一个方向向量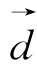
=（1，2），求直线l的点方向式方程.
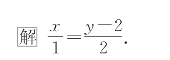
思考：当u=0或v=0时，写出直线l的方程.
u=0时，l：x=x0；v=0时，l：y=y0.
案例3-6是高二解析几何的第一堂课.直线的方程是在学生初中阶段学习了正比例函数和一次函数的基础上进行研究的.学生在学习过程中很容易产生为什么要学习这堂课的疑问.而这堂课是在学生初中阶段直观认识的基础上，将直线的方程进行更加严格的定义和证明，帮助学生明确逻辑推理在得到数学结论、构建数学体系的重要意义.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：数学学科的价值详细阅读
现代科学的的知识体系以观察和数学为中心，为了获得新知，绝大部分科学研究都是通过收集各种观察值，再用数学建模工具整理连接，形成全面的理论数学模型，搭建了数学与外部世界联系的桥梁，是数学应用的重要形式.数学建模素养的数学学科价值不仅在于它是应用数学解决实际问题的基本手段，并且它也是推动数学发展的动力.荷兰著名数学教育家弗赖登塔尔认为，人们在观察，认识和改造客观世界的过程中，运用数学的思想和方法来分析和......
2023-08-17
-
高中数学核心素养与数学学科的价值详细阅读
数学是人类文化的重要组成部分，数学课程反映数学的历史、应用和发展趋势及数学学科的思想体系、创新精神和在人类文明发展中的作用.数学运算是数学学科独有的能力，是解决数学问题的基本手段.除了数学问题本身之外，生产生活的各个领域都需要数学运算来解决问题，诸如经济学、航空航天、材料设备、人工智能、互联网大数据等，都离不开数学运算.在理论研究中，数学运算也发挥着独特的作用，例如，利用数学运算的原理分析解决物理......
2023-08-17
-
高中数学核心素养之逻辑推理攻略详细阅读
某学生回答：“是的.”并给出证明如下：假设当n=k时，等式成立，即2+4+6+……+2k+2（k+1）=k2+k+2+2（k+1），而k2+2k+1+k+1+2=（k+1）2+（k+1）+2，等式也成立.你认为这个学生回答的对吗？......
2023-08-17
-
高中数学核心素养的思维价值详细阅读
对学生来说，数学首先是利用自己的生活经验对数学现象的一种“解读”，这需要的是由数学向学生日常生活的“回归”.但是到了更高阶段的抽象时，已经没有必要每次的运算或者推导都要回归到具体事物间的关系上去.又或者说，除了“解读”外，我们还需要帮助学生由“日常数学”上升到“学校数学”.这其中，蕴含着数学抽象的两个阶段.在数学的学习中，学生一般通过理解抽象性概念，练习公式以及变式，在数学应用中创建抽象化的产物，......
2023-08-17
-
高中数学核心素养的美学价值详细阅读
法国数学家庞加莱曾说：“数学家不单单因为数学有用而研究数学，他研究它还因为他喜欢它，而他喜欢它则是因为它是美丽的.”数学既具有一般意义下美的特点，又有自身独有的美，即所谓的数学美.数学美的内容极其丰富，既有具体、形象和感性的一面，又有形式、抽象和理性的一面.吴军在《数学之美》一文中说，数学之美，首先在于用简单的形式表达复杂而深奥的内容；其次在于数学原理的通用性和普遍性.数学美是一种独特的、兼具震撼......
2023-08-17
- 详细阅读
-
高中数学核心素养：认知事物间的关联价值详细阅读
表征性抽象，时常由事物的表面现象经验性地得到一些结论，这停留在抽象的第一个阶段.而原理性抽象把握的是事物的因果性和规律性的联系.在数学的学习中，往往需要联系事物之间的关系，为数学的高度抽象关系，建构起更加具体形象的认知.章建跃认为，人类的智慧表现在用简单的概念阐明科学的基本问题，用相似的方法解决不同的问题，而数学的方法就是这样的方法.在数学中，自然数不仅打开了数学研究的大门，也为数学推理验证由“有......
2023-08-17
相关推荐