首页理论教育高中数学核心素养：逻辑推理主要表现形式

高中数学核心素养：逻辑推理主要表现形式

2023-08-17 理论教育版权反馈

【摘要】：甲因事耽误了多长时间？当x为何值时，乙行驶的路程比甲行驶的路程多1千米？

逻辑推理的主要表现形式为：掌握推理基本形式和规则，发现问题和提出命题，探索和表述论证过程，理解命题体系，有逻辑地表达与交流.

高中数学学习阶段，逻辑推理素养的表现及水平可以从情境与问题、知识与技能、思维与表达、交流与反思等方面进行考量.要注重情境的合理性，习得的知识与技能的内在逻辑关系，同时也要注意在数学语言表达上的规范性.

在必修板块中的主题一预备知识中有一个单元“常用逻辑用语”.常用逻辑用语是数学语言的重要组成部分，是数学表达和交流的工具，是逻辑思维的基本语言.《普通高中数学课程标准（2017年版）》对这部分内容作了如下描述：“可以帮助学生使用常用逻辑用语表达数学对象、进行数学推理、体会常用逻辑用语在表述数学内容和论证数学结论中的作用，提高交流的严谨性与准确性.”其中必要条件、充分条件、充要条件是学习的重要内容之一.

【案例3-4】用一般情况的结论研究特殊情况

问题：已知a，b，x，y∈（0，+∞）.

pagenumber_ebook=75,pagenumber_book=66

案例3_4中，第（1）问是一般情况，第（2）问是第（1）问的特殊情况，可以运用第（1）问的结论来研究.首先通过演绎推理的方式，对一般情况进行证明，接下来在一般情况得证的基础上，再以此作为工具研究特殊情况.该案例用探索和表述论证的过程作为研究的主线，同时帮助学生理解命题体系的构建.

【案例3-5】图像、函数解析式与实际问题间的内在逻辑关系

问题：甲乙二人骑自行车同时从A地出发，沿同一路线去B地.甲行驶20分钟因事耽误一会儿，事后继续按原速行驶.图3-1所示为甲乙二人骑自行车行驶的路程y（千米）随时间x（分）变化的图像（全程），根据图像回答下列问题.

（1）乙比甲晚多长时间到达B地？

（2）甲因事耽误了多长时间？

（3）当x为何值时，乙行驶的路程比甲行驶的路程多1千米？

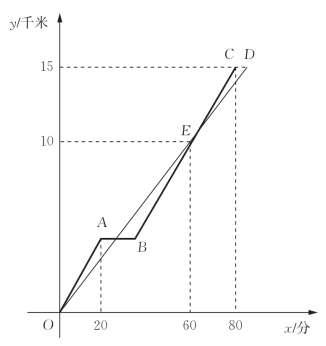
pagenumber_ebook=75,pagenumber_book=66

图3-1

分析该题是在函数图像分析的基础上，对现实情境中发生的问题进行推理，将逻辑推理运用到生活中，体现了数学的应用价值.

解设乙对应的函数为y=k1x（x∈［0，xD］）.

∵E（60，10），∴10=k1×60，∴，即乙对应的函数为.

pagenumber_ebook=76,pagenumber_book=67

（1）设D（xD，5），∴，∴xD=90，90-80=10（分钟），乙比甲晚10分钟；

（2）∵A（20，5），B（40，5），40-20=20（分钟），甲耽误了20分钟；

（3）设线段OD交线段AB于点F（xF，5），∴，∴xF=30，即F（30，5）.

由此可见，乙行驶的路程比甲多1千米的情况只会发生在x∈（30，60）的范围中，

当x∈30，40（］时，∴x=36，

当x∈（40，60）时=1，∴x=48.

故当x为36或48时，乙行驶的路程比甲行驶的路程多1千米.

由案例3-5可以看出，在逻辑推理形式的研究过程当中，发现问题和提出命题是很重要的一部分内容.通过逻辑推理的方式，从情境的角度出发进行提炼，习得图像、函数解析式以及实际问题之间的内在逻辑关系，从而研究和解决问题.