高中数学核心素养：循序渐进的年级渗透

2025-09-29 理论教育版权反馈

【摘要】：从高一到高三，教学要求和教学内容在不断变化，学生的学习能力和探究水平在也成长，因此数学运算素养在各个年级的表现是不同的，但又不是割裂的，它会以螺旋的状态不断上升.《普通高中数学课程标准（2017版）》将数学运算素养划分为3个水平层级，数学运算素养在各个年级里的渐进渗透可以以此为参考依据.【案例2-11】以基本不等式为例感受数学运算的循序渐进背景：课程标准对于基本不等式的要求为：①探索并了解基本不等

从高一到高三，教学要求和教学内容在不断变化，学生的学习能力和探究水平在也成长，因此数学运算素养在各个年级的表现是不同的，但又不是割裂的，它会以螺旋的状态不断上升.《普通高中数学课程标准（2017版）》将数学运算素养划分为3个水平层级，数学运算素养在各个年级里的渐进渗透可以以此为参考依据.

【案例2-11】以基本不等式为例感受数学运算的循序渐进

背景：课程标准对于基本不等式的要求为：①探索并了解基本不等式的证明过程；②会用基本不等式解决简单的最大（小）值问题.《2025年考试手册》（上海卷）对基本不等式的要求是：掌握基本不等式并会用于解决简单问题（属于探究性理解水平）.事实上，高一到高三阶段，我们经常会用到基本不等式的思想去解决问题.

1.高一学段

高一学段是基本不等式的学习理解阶段，能运用基本不等式求解简单的最值问题.

问题：已知a＞0，b＞0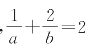 pagenumber_ebook=59,pagenumber_book=50 ，求a+2b的最小值.

分析本题是基本不等式的初级篇，要注意使用条件：一正、二定、三等.需要学生能构造出适合基本不等式的使用结构，本题是“1”的妙用，具有一定的规律性，建议记住此类运算方法和技巧.

2.高二学段

高二学段主要学习的内容有数列、向量、解析几何、复数、矩阵行列式等.虽然基本不等式已经属于学过的知识，但是利用基本不等式作为运算思路求解问题的策略始终贯穿在所学的知识之中.(https://www.chuimin.cn)

分析本题是数列中的最值问题，求解本题的运算方法简单地说有等比数列通项公式、指数方程以及利用基本不等式或者利用整数的性质求最小值.

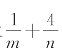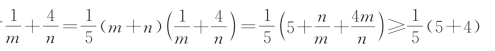
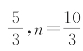易错分析本题的易错点是很多学生误认为：已知m+n=5，求 pagenumber_ebook=59,pagenumber_book=50 的最小值也可以使用基本不等式中“1”的妙用，有.错误在于没有考虑取等条件，上述不等式中，当n=2m时取等，而m+n=5，解得m= pagenumber_ebook=60,pagenumber_book=51 ，与m、n∈N矛盾.

经过运算和判断，可以体会到基本不等式是把双刃剑，用好了会给求解带来很大的便捷，若失误了则损失惨重，所以必须要考虑仔细周到.

3.高三学段

高三学段是对所学知识综合运用的阶段，此时，求解一个问题可能需要多种运算手段，运算思路也变得灵活多变，需要学会判断、学会选择.

问题：对于函数f1（x）、f2（x）、h（x），如果存在实数a、b使得h（x）=af1（x）+bf2（x），那么称h（x）为f1（x）、f2（x）的生成函数.设f1（x）=x（x＞0），f2（x）=，a＞0，b＞0，生成函数h（x）图像的最低点坐标为（2，8），试问是否存在最大的常数m，对于任意正实数x1、x2且x1+x2=1，h（x1）h（x2）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由.

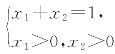分析本题是函数的综合问题，求解本题的运算思路是先得出函数，利用题意以及基本不等式得出a=2、b=8，然后利用基本不等式求出h（x1）h（x2）在条件 pagenumber_ebook=60,pagenumber_book=51 下的最小值，即可得出m的取值范围，进而求出m的最大值.

通过案例2_11中基本不等式在3个学段的中的运用，可以感受到随着学段上升，运算能力的综合性也更强，求解问题时运算法则和运算思路的选择更是多样，这是一个循序渐进的思维过程，学生要注意学习的连续性和综合性.

高中数学核心素养：循序渐进的年级渗透

相关推荐