基于数学核心素养的教学就是要培养学生用数学的眼光看世界，因此，数学教师首先要能够用数学的眼光看世界，用数学的眼光看身边的事物，并在平时教学中能够注重基于教学内容的实际背景向学生渗透数学与实际生活的联系.（一）数学建模的教学原则数学建模活动作为《普通高中数学课程标准（2017年版）》课程内容之一，要求以课题形式，小组合作方式开展教学，最终以研究报告或小论文等多种形式呈现.数学建模活动的主要特征体现在......
2023-08-17
高中数学核心素养：数学运算渗透
【摘要】：数学教学与学习会经历课前准备、课上磨合、课后巩固3个阶段.针对每个阶段，教师都会设计不同的环节以提升数学学习的效果.那么，数学运算素养如何在各个教学环节中渗透呢？
数学教学与学习会经历课前准备、课上磨合、课后巩固3个阶段.针对每个阶段，教师都会设计不同的环节以提升数学学习的效果.那么，数学运算素养如何在各个教学环节中渗透呢？下面将以案例的形式做具体阐述.
（一）数学运算素养在课堂提问环节中的渗透
提问是开启学生创造思维能力的最直接最简便的教学方法，也是教师借以接受学生反馈信息的一种有效手段.提问教学关键在与设计问题，围绕数学运算素养的培养，所设计的问题可以围绕运算思路的选择、运算法则的记忆、运算对象的确定展开.
教学是一门语言的艺术，课堂上教师讲什么？怎么讲？问什么？怎么问？其实非常重要，讲的内容要能使学生自发地生成互动，问的内容则要让学生主动地生成思考.运算是数学的基础，所以在讲解问题时，教师可以从运算的角度出发，围绕着运算思路和运算方法设置问题，让学生在运算的过程中体会解决问题的方法和策略，悟到处理复杂的切入点，构建条件与条件、条件与结论之间的关联.
（二）数学运算素养在课堂导入环节中的渗透
导入是新的教学内容或教学活动开始前，引导学生进入学习状态的教学行为方式.精彩的导入可以为整堂课的教学奠定良好的基础.课堂导入的形式是多样的，根据授课内容而产生变化.从数学运算的角度进行课堂导入，也是常见的方式之一.
【案例2-10】半角公式（第一课时）的导入
课堂实录
师：（情境设置）生活中，上坡下坡、上楼下楼是难免的，这对于正常人而言是一件不费劲的事，但对于那些肢体有残疾的人来说可谓“困难重重”.在市委市政府的关怀下，新修建了许多无障碍设施，旧区无障碍改造的工程也频频竣工.细数身边的无障碍设施，残疾人坡道（见图2-8）算是其中一种最常见的了.
坡道的结构很简单，我们可以用直角三角形来模拟，如图2-9所示.
图2-8
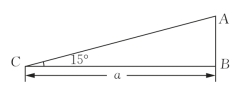
图2-9
师：假设坡角的大小是15°，B、C之间的距离是a，那么斜坡CA的长度是多少？
生
师：不借助计算器如何计算cos15°？
生：可以利用cos30°=2 cos2 15°-1，通过解方程求出cos15°.
师：（肯定学生的解题方法，进一步提出问题）解法中，我们已知cos30°求cos15°，将其一般化，可以理解为已知cosα求
，请大家思考：怎么来求
呢？
生：由余弦的二倍角公式得
，所以
师：类似地，能否在已知cosα的前提下求
的值呢？
生：再由余弦的二倍角公式得
师：那么，
呢？
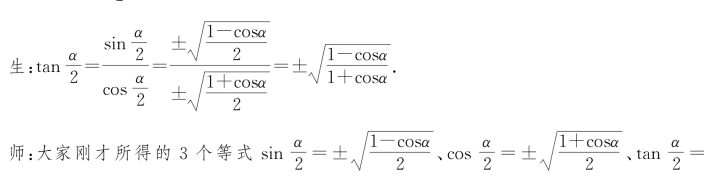
案例2_10中，教师从生活中的实际出发，抽象数学数学模型，根据本节课的教学目标，设计数学问题，用“追问”的形式，带动学生思维高速运转，以数学运算为抓手，从特殊到一般推导半角公式，引出本节课的教学内容.这样的引入，很自然地将德育教育融入数学课堂.在此情景下，学生们的自主学习热情被调动了起来，对半角公式的记忆更加持久与深刻.
（三）数学运算素养在课堂板书环节中的渗透
板书是指在课堂教学过程中，教师出于教学目的的需要，把精心设计的巧妙美观的文字、数学公式和符号以及所画的图表展示在黑板上.板书的内容构成可以是事先设计好的，也可以是课上师生之间的灵光的闪现.
数学运算是课堂教学中必不可少的活动之一，因此在板书设计的环节，也需要有所体现，要注意以下几方面.
1.计划性
留在黑板上文字的应该是一节课中最重要的部分，因此在课前需要有设计，板书分为主板书和辅助板书，主板书应放在中央显著位置，辅助板书应放在边角作为教学补充.运算性质、运算公式等可以放在显著位置，典型例题的求解、学生答题的痕迹可以放在边角作为补充.
2.规范性
板书是给学生做示范，因此板书要写规范字，字迹要工整，绘图要正确、美观、严格规范.相应地，数学运算的板书要体现规范的答题过程，不冗长、不跳步，对关键步骤可以用不同颜色的粉笔做出标示.
3.完整性
一般一节课告一段落时，主要内容要完整地保留在黑板上，使学生对全节课的内容有一个连贯的全面认识.
4.针对性
板书要突出重点，其结构要与讲授的内容大体一致.若过于繁细，则易使重点不突出，学生抓不住东西，造成学生疲劳，影响教学效果；若过于简粗，则不能起提纲挈领，揭示教学主要内容的作用，不利于学生理解和所掌握所学知识.特别是习题课，会有大量的运算要求，建议教师选择通性通法作为重点内容留在主板书上，挑选易错问题和共性问题放在辅助板书上.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：数学抽象素养渗透于学习详细阅读
设计意图 生成分类加法计数原理的数学符号公式.问题2：观察后3个问题的计数方式，有什么共同点？设计意图 归纳出分类加法计数原理与分步乘法计数原理的异同点.案例1-8中，教师将核心问题从横向、纵向两个思维方向进行比较，设计出4个具有高阶思维的连续问题，这样的设计让学生在具体的生活情境中，通过从特殊到一般和类比的思维方法，归纳并形成简单的数学命题，进而培养了学生的抽象概括能力.......
2023-08-17
-
高中数学核心素养：循序渐进的年级渗透详细阅读
从高一到高三，教学要求和教学内容在不断变化，学生的学习能力和探究水平在也成长，因此数学运算素养在各个年级的表现是不同的，但又不是割裂的，它会以螺旋的状态不断上升.《普通高中数学课程标准（2017版）》将数学运算素养划分为3个水平层级，数学运算素养在各个年级里的渐进渗透可以以此为参考依据.【案例2-11】以基本不等式为例感受数学运算的循序渐进背景：课程标准对于基本不等式的要求为：①探索并了解基本不等......
2023-08-17
-
高中数学核心素养：数学抽象渗透各学科详细阅读
数学抽象在数学各章节都有充分的体现.这里以立体几何部分为例做一个分析.我们知道，几何学研究现实世界中物体的形状、大小和位置关系.位置是空间的最原始概念，几何学中用点来标记位置，点就是位置的抽象化.连接空间两个位置的通路是空间第二个原始概念，几何学将之抽象为从一个点到另一个点的连线.两点之间的所有连线中，有且只有一条最短，我们将它称为线段.“两点之间线段最短”是欧氏空间的基本特性（其他空间都不具有这......
2023-08-17
-
高中数学核心素养：逻辑推理渗透数学学习详细阅读
逻辑推理素养作为高中数学六大核心素养之一，承载着落实数学学科严谨性特征的重要责任.在每一个数学学习的环节中，都可以将逻辑推理素养进行合理渗透，从而提高学生的逻辑推理能力.数列的最值初步研究1.预习演练问题反思 ①类比函数的最值，如何定义数列的最值？问题：设等差数列｛an｝的前n项和为Sn，已知a1＜0，S8=S13，则当n取何值时，Sn最小？......
2023-08-17
-
高中数学核心素养详解详细阅读
通过图形的表征与变换，理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化，都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.【案例4-15】构造几何模型，破解思维瓶颈问题：设点P是函数的图像上的任意一点，点Q（2a，a-3），（a∈R），则|PQ|的最小值为__________.解：函数的图像是以C（1，0）为圆心，半径等于2的圆在x轴以下的半圆，含点（-1，0）、（3，0）.......
2023-08-17
-
高中数学核心素养：数学建模思想在课程中的渗透详细阅读
【案例5-4】函数模型结构特征运用在高中阶段函数部分的学习中，学生已经熟知的函数模型有正比例函数、反比例函数、一次函数、二次函数、指数函数、对数函数、幂函数等，其实除了这些基本模型外，在学生的学习过程中，还有很多函数具有较好的代表性.通过分析这些函数的结构特征，可以构建相应的结构型数学模型来解决具有共同特征的某一类问题.对比这两个题目在结构特征上的共性，可以发现其题目设问结构基本一致；题目中涉及的......
2023-08-17
-
高中数学核心素养：必备知识中的数学运算详细阅读
数学运算素养作为基本素养存在于各个章节之中，是不可忽视的重要能力之一.从必备知识角度考察数学运算素养，可以关注以下原则：由具体到抽象，由法则到算理，由常量到变量，由单向思维到逆向、多向思维.过程中，运算法则是基础，解决问题的思路是目标.在评价中，还应警惕学生片面追求运算速度，只有在理解的基础上，形成好的思维品质，速度才有意义.【案例2-18】平面中轨迹方程的求法解析几何问题是高考的必考问题，既有能......
2023-08-17
相关推荐