基于数学核心素养的教学就是要培养学生用数学的眼光看世界，因此，数学教师首先要能够用数学的眼光看世界，用数学的眼光看身边的事物，并在平时教学中能够注重基于教学内容的实际背景向学生渗透数学与实际生活的联系.（一）数学建模的教学原则数学建模活动作为《普通高中数学课程标准（2017年版）》课程内容之一，要求以课题形式，小组合作方式开展教学，最终以研究报告或小论文等多种形式呈现.数学建模活动的主要特征体现在......
2023-08-17
数学核心素养贯穿教学活动
【摘要】：师：相信大家都有这样的体会，与圆相关的问题从计算量来看会比其他问题小，从复杂程度上看也会比其他问题简单些.从某种程度上说，椭圆可以通过圆上的点经过坐标变换而得，所以，这个问题能不能利用圆的知识求解呢？
课程标准提出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必须的数学基础知识、基本技能、基本思想、基本活动经验；提高从数学角度发现和提出问题、分析和解决问题的能力（简称“四基四能”）.根据运算法则，通过运算得出正确的结果，这是数学基本技能；探索运算思路，选择最合适有效的办法解决问题，这是分析和解决问题的能力，也是基本活动经验的体现.数学教学活动应关注“四基四能”的培养，数学运算作为数学学科的基本特征，渗透于数学教学各种活动中.
（一）梳理学生运算时的常见错误
受个人习惯和思维障碍的影响，经常会犯雷同的错误.教师需要将学生的常见错误进行梳理和归纳，只有发现学生运算时的常见错误，方能对症下药，增强数学运算素养培养的针对性，从而提高素养培养的有效性.
【案例2-8】指数对数运算常见错误举例
1.化简运算错误导致错误解答
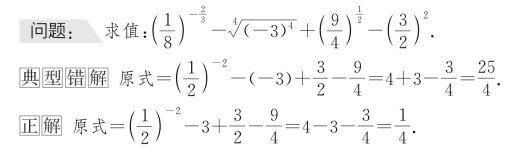
2.运算法则错误
问题：已知x，y为正实数，则正确的是（ ）.
典型错解 B
正解 D
错因 错误原因在于指数和对数运算法则运用错误.
3.忽略定义域或定义域计算出错
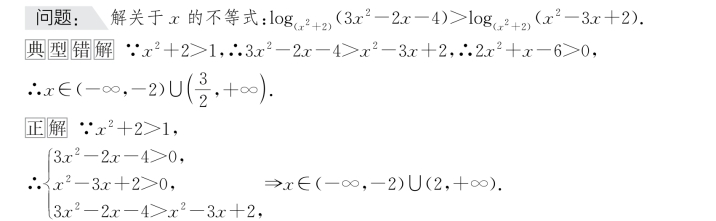
错 因错误在于求解对数不等式时忽略了对数函数的定义域，对于函数问题，必须遵循“定义域优先”的原则.
（二）达成对数学运算重要性的共识
有的学生认为数学问题有思路即可，至于能否正确计算出结果，不是最重要的.就是由于这种想法的普遍存在，导致学生的数学运算素养欠缺，因此在教学活动中，教师需要避免让学生出现被动接受的情况，鼓励学生成为运算活动的参与者，要和学生达成共识，在教与学的过程中设定共同的目标，并一起为之努力.
（三）涉及数学运算素养提升的有效途径
重视课堂与课外相结合，关注理论学习与实践操作相结合.教师可结合教学内容设置数学题，引导学生将学习过程转化为运算的过程，一方面让学生通过运算来掌握课堂知识，另一方面也培养学生的运算能力.
【案例2-9】关注一题多解，激发思维递进
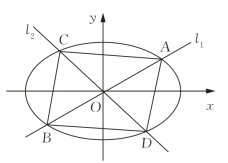
图2-6
问题：如图2-6所示，已知椭圆x2+2y2=1，过原点的两条直线l1和l2分别与椭圆交于点A、B和C、D，记得到的平行四边形ABCD的面积为S.
（1）设A（x1，y1），C（x2，y2）.用A、C坐标表示点C到直线l1的距离，并证明S=2|x1y2-x2y1|；
（2）设l2与l2的斜率之积为
，求面积S的值.
课堂实录
师：请大家仔细审题，尝试完成第（1）小题.
生1：由题易知A、C两点的横坐标不能同时为零，又考虑到斜率是否存在，故分以下两种情况讨论：
i 当A、C两点的横坐标有一个为零时，不妨设x1=0，x2≠0，此时C到直线l1的距离d=|x2|，平行四边形ABCD的面积为S=2|x2y1|；
生2：合理选择设直线的方法可以简化本题，所以我觉得点法向式直线方程会起到简化作用.已知直线l1的法向量是（-y1，x1），因此设直线l1的方程为-y1x+x1y=0，则点C到l1的距离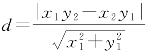
，接下来就和上一位同学的做法相同.
师：很好，那么第（2）小问呢？
师：相信大家都有这样的体会，与圆相关的问题从计算量来看会比其他问题小，从复杂程度上看也会比其他问题简单些.从某种程度上说，椭圆可以通过圆上的点经过坐标变换而得，所以，这个问题能不能利用圆的知识求解呢？
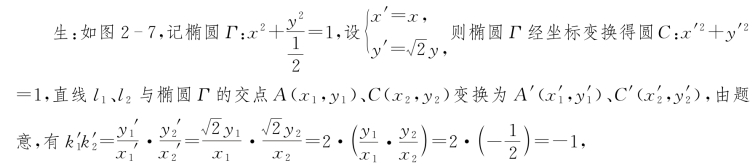
所以，在圆C中l1'⊥l2'，则圆中四边形A'B'C'D'面积
，
因此，椭圆中四边形ABCD面积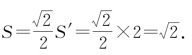
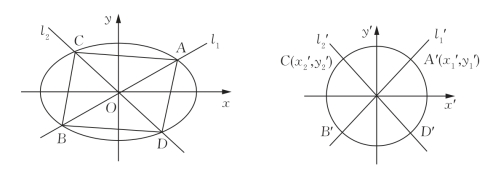
图2-7
由案例2_9可以看出，基于落实数学核心素养的教学设计，需要在课堂活动形式和内容指向上做出根本性的调整.学生应有更多自主探究时间、问题空间和学习场域的探究活动.具有挑战性学习问题是探究活动的缘起和目标导向，如案例2_9中，通过一道高考题，教师步步设问，让学生深入思考椭圆与圆的性质之间的关系，借助于数学运算，培养学生的直观想象、逻辑推理等核心素养.
有关高中数学核心素养的文章
- 详细阅读
-
小学数学教学方法选配：提升核心素养详细阅读
教学有法但无定法，面对具体的教学内容教师充分发挥主观能动性，选择甚至创造适当的教学方法进行教学。判断的标准就是有利于发展核心素养，有利于教学的目标的达成。统计学的发展与数据分析工具的发展联系紧密。此时教师可以提示学生利用方格纸、横格本等来画图，扫除画图的障碍，让学生把精力主要集中在如何用图更好地表示数据上。通过数据分析体验随机性需要大量的数据。教学中可以采用分组实验再将数据汇总的方法。......
2023-08-07
-
高中数学核心素养：直观想象在教学活动中的渗透详细阅读
在数学素养的生成教学策略上，许多国家都倡导用数学活动促进学生数学素养的生成.不少专家提倡，数学学习活动应当具有愉快感和充实感，能体现学生学习过程中的多样性和个性化，给予学生更多的自由发展空间.立体几何序言课课堂实录师：请同学们用6根长度相等的牙签（或火柴）搭正三角形，试试看，最多搭成几个正三角形？......
2023-08-17
-
小学数学学科核心素养培养的教学表现详细阅读
下面将结合教材谈一谈数据分析观念的三个主要方面在教学中的表现。教材习题中安排的统计活动体现了对经历数据分析过程的要求，这些统计活动过程随学段升高更加完整。图6图73.3通过数据分析体验随机性统计与概率都是研究随机现象的学科，但是它们是从不同角度研究如何刻画随机现象的。《义务教育数学课程标准》提出通过数据分析体会随机性就是指用统计的方法研究随机现象。......
2023-08-07
-
基于核心素养的小学数学教学研究成果详细阅读
《义务教育数学课程标准》把“空间观念”和“几何直观”作为十大核心词之二提出，《普通高中数学课程标准》将直观想象作为六大数学核心素养之一提出，可见直观想象在数学学习中的重要性，直观想象是对几何直观、空间想象和空间观念的融合与发展。......
2023-08-07
-
高中数学核心素养详解详细阅读
通过图形的表征与变换，理解图形的特征、简化运算过程、将“数”与“形”的问题自由转化，都体现了直观想象核心素养在数学问题解决过程中关键能力的作用.【案例4-15】构造几何模型，破解思维瓶颈问题：设点P是函数的图像上的任意一点，点Q（2a，a-3），（a∈R），则|PQ|的最小值为__________.解：函数的图像是以C（1，0）为圆心，半径等于2的圆在x轴以下的半圆，含点（-1，0）、（3，0）.......
2023-08-17
-
高中数学核心素养：数学抽象素养的扩展详细阅读
（一）抽象1.理想化的抽象理想化的抽象即指抽象层次性的简约阶段，由实际的事物或现象引出抽象概念的方法，其中包括对于真实事物或现象的简约化与完善化，从而得出的数学概念与现实原型未必完全符合，如“没有大小的点”“没有宽度的线”“没有厚度的面”等几何概念都是简约化的结果.平面几何中已经证明任意三角形三个角的平分线交于一点，但真实世界的经验告诉我们，无论绘图员多么细心、采用多么精确的工具，他所画图形中的三......
2023-08-17
-
数学运算素养：培养思维，提升核心素养详细阅读
思维是指理性认识的过程，是人脑对客观事物间接的和概括的反映，属于人脑的基本活动形式.数学思维则是指用数学思考问题和解决问题的思维活动形式.数学思维既能动地反映客观世界，又能动地反作用于客观世界.数学运算中强调探究运算思路，通过探究可以激发思维的灵活性、广阔性，锻炼思维的敏捷性和深刻性，形成思维的独创性、批判性和灵活性.问题：书架上有5本书，现在再插入3本不同的书，有多少种不同的方案？......
2023-08-17
相关推荐