表征性抽象，时常由事物的表面现象经验性地得到一些结论，这停留在抽象的第一个阶段.而原理性抽象把握的是事物的因果性和规律性的联系.在数学的学习中，往往需要联系事物之间的关系，为数学的高度抽象关系，建构起更加具体形象的认知.章建跃认为，人类的智慧表现在用简单的概念阐明科学的基本问题，用相似的方法解决不同的问题，而数学的方法就是这样的方法.在数学中，自然数不仅打开了数学研究的大门，也为数学推理验证由“有......
2023-08-17
高中数学核心素养与认知事物关联的价值
【摘要】：发展数学素养是时代的需要，聚焦数学核心素养是数学课程改革的趋势.我们所处的是一个大数据时代，数字化程度高，信息交流广泛，而数学正直接或间接地渗透到社会生活的各个领域，广泛地影响着人们的生活.数学运算是用数学的方法分析事物之间的关系，用符号、字母表示事物的形态，用数据、图标、关系式表示事物之间的联系，通过事物之间的联系探寻解决问题的运算思路，制定运算法则准确计算所产生的结果，这都体现着数学运算对认知
发展数学素养是时代的需要，聚焦数学核心素养是数学课程改革的趋势.我们所处的是一个大数据时代，数字化程度高，信息交流广泛，而数学正直接或间接地渗透到社会生活的各个领域，广泛地影响着人们的生活.
数学运算是用数学的方法分析事物之间的关系，用符号、字母表示事物的形态，用数据、图标、关系式表示事物之间的联系，通过事物之间的联系探寻解决问题的运算思路，制定运算法则准确计算所产生的结果，这都体现着数学运算对认知事物方面起到的作用.
数学运算在其他学科中也发挥着重要的作用.如牛顿的力学巨著《自然哲学的数学原理》运用微积分工具，严格推导证明了开普勒行星运动三大定律、万有引力定律等一些结论.再如目前国际通用的地震震级标准——里氏震级，它是根据离震中一定距离观测到的地震波幅度和周期，并且考虑从震源到观测点的地震波衰减，经过一定公式计算出来的震源处地震的大小.还有，其他学科如生物学中运用微分方程、线性代数、概率论、数理统计、抽象代数等，都是在利用数学知识形成运算思路，提供运算方法.
【案例2-6】缉私问题
问题：某海警基地码头O的正西方向30海里处有海礁界碑A，过点A且与AO成60°角（即北偏东30°）的直线l为此处的一段领海与公海的分界线（如图2-4所示）.在码头O的正西方向且距离O点12海里的领海海面P处有一艘可疑船停留，基地指挥部决定在测定可疑船的行驶方向后，海警巡逻艇从O处即刻出发.若巡逻艇以可疑船的航速的λ倍（λ＞1）前去拦截，假定巡逻艇和可疑船在拦截过程中均未改变航向航速，将在点Q处截获可疑船.
（1）若可疑船的航速为10海里/小时，λ=2，且可疑船沿北偏西30°的方向朝公海逃跑，求巡逻艇成功拦截可疑船所用的时间.
（2）若要确保在领海内（包括分界线）成功拦截可疑船，求λ的最小值.
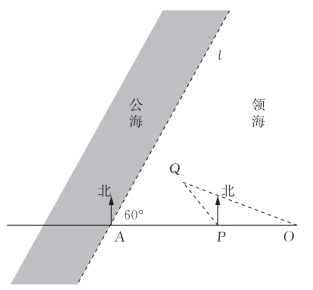
图2-4
分析上教版高二数学教材里有一探究与实践课题：追捕走私船.探究的内容是在某海域中缉私船追击走私船的线路、轨迹等问题，本题就是基于该探究实践活动的改变问题.需要学生在理解题意的基础上，选择合理的算法，按要求展开计算，从而得到正确的判断.
（1）因为巡逻艇的航速是可疑船的航速的2倍，可疑船的航速为10海里/小时，所以巡逻艇的航速为20海里/小时.由图2-4可知，OQ=2PQ，设PQ=a，则OQ=2a，又可疑船沿北偏西30°的方向朝公海逃跑，所以∠QPO=120°.
在△OPQ中，有OQ2=OP2+PQ2-2OP·PQ cos∠OPQ，即4a2=a2+144-2×12a cos120°，得a2-4a-48=0，解得
（负值舍去）.所以
小时.
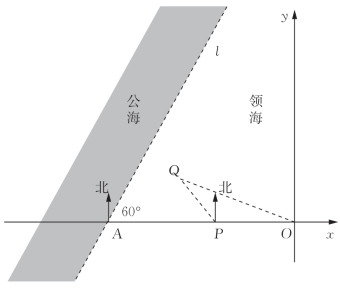
图2-5
（2）以O为坐标原点，AO的方向为x轴的正方向，建立如图所示的平面直角坐标系，如图2-5所示则P（-12，0）、A（-30，0）.设Q（x，y），因为巡逻艇的航速是可疑船的航速的λ倍，所以OQ=λPQ，故x2+y2=λ2[（x+12）2+y2]，即
.
故可疑船被截获的轨迹是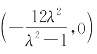以
为圆心，以
为半径的圆.又直线l的方程为y
.
要确保在领海内（包括分界线）成功拦截可疑船，则圆心
下方，且Q的轨迹与直线l至多只有一个公共点，所以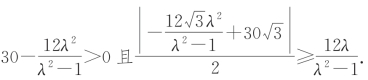
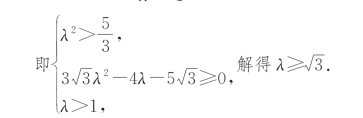
故要确保在领海内（包括分界线）成功拦截可疑船，则
.
案例2-6所示即为利用求动点的运行轨迹，结合直线与圆的位置关系，解决实际问题.选择直线与圆锥曲线运算的通法，通过数学运算判断缉私过程中的可能会遇到的问题，并解决问题.可见解决该题除了需要数学运算素养外，还需要数学抽象、数学建模、逻辑推理等多素养的综合运用.
有关高中数学核心素养的文章
- 详细阅读
-
高中数学核心素养：直观想象的认知关联价值详细阅读
提升学生直观想象核心素养，在帮助他们认知事物之间的关联方面具有非同一般的价值.通过直观想象素养的培养，帮助学生通过数学间的内在联系，将数学问题图像化，分析问题的本质关联，从而将问题理解得更为深入，问题的解决得以顺利进行.三角函数的周期性1.问题的提出“离离原上草，一岁一枯荣，野火烧不尽，春风吹又生”蕴含了什么数学知识？......
2023-08-17
-
高中数学建模素养的认知价值详细阅读
数学建模就是要培养学生用事物相互联系和发展变化的观点来分析问题，从而认识事物之间是相互联系和有规律地变化着的.数学建模是数学与其他领域之间建立联系的方法.数学建模的过程就是提出一个问题，然后细化问题，最后以精确的数学术语表述.一旦问题变成数学问题，就要使用数学来找到答案，并且最后必须逆转这一过程（这是很多人忘记的部分），将数学解转换回对原始问题的可理解的，有意义的答案.从思想上来说，数学建模是构建......
2023-08-17
-
高中数学核心素养的思维价值详细阅读
对学生来说，数学首先是利用自己的生活经验对数学现象的一种“解读”，这需要的是由数学向学生日常生活的“回归”.但是到了更高阶段的抽象时，已经没有必要每次的运算或者推导都要回归到具体事物间的关系上去.又或者说，除了“解读”外，我们还需要帮助学生由“日常数学”上升到“学校数学”.这其中，蕴含着数学抽象的两个阶段.在数学的学习中，学生一般通过理解抽象性概念，练习公式以及变式，在数学应用中创建抽象化的产物，......
2023-08-17
-
高中数学核心素养与数学学科的价值详细阅读
数学是人类文化的重要组成部分，数学课程反映数学的历史、应用和发展趋势及数学学科的思想体系、创新精神和在人类文明发展中的作用.数学运算是数学学科独有的能力，是解决数学问题的基本手段.除了数学问题本身之外，生产生活的各个领域都需要数学运算来解决问题，诸如经济学、航空航天、材料设备、人工智能、互联网大数据等，都离不开数学运算.在理论研究中，数学运算也发挥着独特的作用，例如，利用数学运算的原理分析解决物理......
2023-08-17
-
高中数学核心素养及其学科价值详细阅读
对于学科来说，抽象是数学的首要特征，抽象为推理提供了对象，为模型提供了依据，为数学的广泛应用提供了基础.两种事物，如果有相同的量或形，便可用相同的数学方法，因而数学必然、也必须是抽象的.对于育人来讲，“数学虽不研究事物的质，但任一事物必有量和形，所以数学是无处不在、无时不用的”.因而学生经历数学的抽象，不仅由此生成了数学的研究内容，更具普遍意义的是抽象的过程，能让学生学习如何从量或形的视角去观察、......
2023-08-17
-
高中数学核心素养的美学价值详细阅读
法国数学家庞加莱曾说：“数学家不单单因为数学有用而研究数学，他研究它还因为他喜欢它，而他喜欢它则是因为它是美丽的.”数学既具有一般意义下美的特点，又有自身独有的美，即所谓的数学美.数学美的内容极其丰富，既有具体、形象和感性的一面，又有形式、抽象和理性的一面.吴军在《数学之美》一文中说，数学之美，首先在于用简单的形式表达复杂而深奥的内容；其次在于数学原理的通用性和普遍性.数学美是一种独特的、兼具震撼......
2023-08-17
-
高中数学核心素养：数学学科的价值详细阅读
现代科学的的知识体系以观察和数学为中心，为了获得新知，绝大部分科学研究都是通过收集各种观察值，再用数学建模工具整理连接，形成全面的理论数学模型，搭建了数学与外部世界联系的桥梁，是数学应用的重要形式.数学建模素养的数学学科价值不仅在于它是应用数学解决实际问题的基本手段，并且它也是推动数学发展的动力.荷兰著名数学教育家弗赖登塔尔认为，人们在观察，认识和改造客观世界的过程中，运用数学的思想和方法来分析和......
2023-08-17
相关推荐