高中数学核心素养的美学价值

2025-09-29 理论教育版权反馈

【摘要】：法国数学家庞加莱曾说：“数学家不单单因为数学有用而研究数学，他研究它还因为他喜欢它，而他喜欢它则是因为它是美丽的.”数学既具有一般意义下美的特点，又有自身独有的美，即所谓的数学美.数学美的内容极其丰富，既有具体、形象和感性的一面，又有形式、抽象和理性的一面.吴军在《数学之美》一文中说，数学之美，首先在于用简单的形式表达复杂而深奥的内容；其次在于数学原理的通用性和普遍性.数学美是一种独特的、兼具震撼

法国数学家庞加莱曾说：“数学家不单单因为数学有用而研究数学，他研究它还因为他喜欢它，而他喜欢它则是因为它是美丽的.”数学既具有一般意义下美的特点，又有自身独有的美，即所谓的数学美.数学美的内容极其丰富，既有具体、形象和感性的一面，又有形式、抽象和理性的一面.吴军在《数学之美》一文中说，数学之美，首先在于用简单的形式表达复杂而深奥的内容；其次在于数学原理的通用性和普遍性.数学美是一种独特的、兼具震撼力的美，本质上包含了主观意义上的数学美与客观意义上的数学美两个方面的含义，即数学美既是人的主观感受与思维表达，又是内蕴于客观世界的现实存在.

一种数学理论，一个数学体系的形成，都要经过多级次，多层次，多种形式（理想化、模式化、精确化、自由化、形式化）的从最初的感性认识和初步抽象到理性抽象，从不太完善形式向比较完善形式，从不太完美形式到比较完美形式的过渡.这个不断走向美的过程正体现出数学的“简洁美”“统一美”“对称美”“符号美”等.数学中的抽象的方法和结果（数学发现、数学发明、数学创造）的真伪性与价值往往可以通过以上所述的“数学美”的标准来鉴别.同时此标准也揭示了数学美的表现特征：简洁性（即数学的符号美、抽象美、统一美）、和谐性（即数学的和谐美、对称美、形式美）、奇异性（即数学的奇异美、朦胧美、常数美）.我们说数学中的创造、发明或发现的过程实际也是审美过程，数学中的创造、发明或发现的结果实际上也是抽象美的结果.

在初等数学中就可以找到很多体现数学美的具体例子.它们都是使用最基本的思维方法——抽象得来的.

【案例1-6】万能公式

在体积计算中的所谓的“万能公式”，它能简洁、统一地应用于棱（圆）柱、棱（圆）锥、棱（圆）台的体积计算，即

其中h为相应几何体的高，S和S'则分别为其上下底的面积.(https://www.chuimin.cn)

数学家引入抽象的算法符号以避免繁杂的运算.正是为了避免重复的加法运算，人们才引进了乘法.如4+4+4+4+4+4+4=4×7.类似地，幂的引进则是为了避免重复的乘法，如4×4×4×4×4×4×4=47.类似的还有，数学各种算式公式的发展与简化，数学概念定理的高度概括和凝练.因此，数学抽象是数学学科美的基本内容.

在数学中人类的本质力量正是借助于抽象得到了最大限度的发挥，现代的数学家们依靠抽象与想象“建造”出了一个宏伟无比而又十分精巧的“数学世界”，达到了最大的纯粹性、深刻性、精巧性、严密性、清晰性、能动性.故此，数学家们以数学抽象为美是十分自然的，并且这在很大程度上就是对于人类自身本质力量的赞美.如今培育学生的数学抽象素养，在美学方面，更多地是希望学生具备发现和欣赏数学抽象所带来的事物的简洁、统一和纯粹，而非顽固地训练和无感情的追求效率.

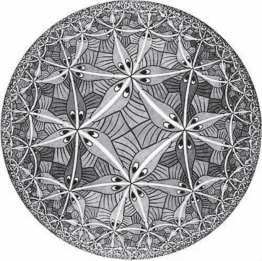
pagenumber_ebook=23,pagenumber_book=14

图1-2

若你无法体会到数学理论、公式所诠释的美，那么荷兰画家埃舍尔艺术性的创作，仿佛使人无法拒绝为之着迷.《圆极限》是埃舍尔众多数学化艺术品种的代表作，如图1-2所示.画中的事物不妨看作是鱼，我们会惊奇地发现：圆是有边界的，而里面的鱼却是无限地多.事实上，对于里面忙碌游动的鱼来说，这个圆却又是无限地大，因为它们远离圆中心，越来越小，慢慢在我们眼际消失，我们不能够望其尽处.埃舍尔本人很欣赏“这个无限而有界的平面世界的美”.

在数学里，无限是一个重要的概念，有其明确的界定.从古希腊的欧多克斯（Eudoxus of Cnidos）用“穷竭法”平息了数学史上第一次数学危机开始，牛顿（Newton）、莱布尼茨（Leibniz）发明微积分，康托尔（G.Cantor）创立集合论，歌德尔（Godel）发现不完备定理，芒德布罗（B.B.Mandelbrot）创立分形理论等，数学家们乐此不疲地运用“无限”这一主题.可以说，无限成了数学中一道亮丽的风景线.关于无限的数学，是人类智慧的结晶，是数学高度抽象的一种表现.如今，却可以由欣赏衣服美妙的艺术创作来实实在在的感受到，这体现出数学抽象激发出的数学美内蕴于客观世界而现实存在.

高中数学核心素养的美学价值

相关推荐