高中数学核心素养的思维价值

2023-08-17 理论教育版权反馈

【摘要】：对学生来说，数学首先是利用自己的生活经验对数学现象的一种“解读”，这需要的是由数学向学生日常生活的“回归”.但是到了更高阶段的抽象时，已经没有必要每次的运算或者推导都要回归到具体事物间的关系上去.又或者说，除了“解读”外，我们还需要帮助学生由“日常数学”上升到“学校数学”.这其中，蕴含着数学抽象的两个阶段.在数学的学习中，学生一般通过理解抽象性概念，练习公式以及变式，在数学应用中创建抽象化的产物，

对学生来说，数学首先是利用自己的生活经验对数学现象的一种“解读”，这需要的是由数学向学生日常生活的“回归”.但是到了更高阶段的抽象时，已经没有必要每次的运算或者推导都要回归到具体事物间的关系上去.又或者说，除了“解读”外，我们还需要帮助学生由“日常数学”上升到“学校数学”.这其中，蕴含着数学抽象的两个阶段.

在数学的学习中，学生一般通过理解抽象性概念，练习公式以及变式，在数学应用中创建抽象化的产物，历经数学符号的发展和应用，强化数学思维.在数学抽象素养的培育过程中，将使得学生具备看待事物时持有大局观，解决繁杂问题时具有特殊角度思考的能力以及正难则反不拘于模式的思辨能力.数学抽象素养一般表现在对一类事物非本质属性的摒弃和对其共同本质特征的反映.

【案例1-4】抽象思维

问题：集合A={1，2，3，…，10}.

（1）设A的3元素的子集个数为n，求n；

（2）设A的3元素的子集中，3个元素的和分别为a1，a2，…，an，求a1+a2+…+an的值.

分析本题主要考查学生的排列组合知识，考查学生的数学抽象，逻辑推理和数据分析能力.尤其是第二问中，如何求出所有3元素子集中元素的和是个难点.面对众多数据求和，学生往往会一筹莫展.需要找寻子集中元素分布的规律，去除众多数据求和的干扰，抓住主线，确定每个元素出现的次数，这也是“加减”低阶运算发展到“乘除”高阶运算的抽象思维，可以用更加高明和简单的方式来解决问题.很明显，这个问题的解决在于排除数据干扰、化繁为简，关注关键元素出现的次数，也即是含有确定包含某个元素的子集个数.

解（1）；

（2）A的3元素的子集中，含有元素1的三元素子集有 pagenumber_ebook=19,pagenumber_book=10 个.

依此类推，1～10每个元素在三元素子集中出现的次数均为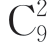 pagenumber_ebook=19,pagenumber_book=10 ，

因此，a1+a2+…+an=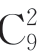 pagenumber_ebook=19,pagenumber_book=10 （1+2+…+10）=1980

对以上问题，就有学生提出以下算式来解决：a1+a2+…+an=（33÷2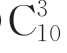） pagenumber_ebook=19,pagenumber_book=10 =1980，其中33÷2指的是元素之和最小的三元素子集{1，2，3}与和最大的三元素子集{8，9，10}的元素之和的平均数，该生把33÷2当做是3元素子集元素之和的平均数，乘上子集的个数来解决问题.其中参照的是等差数列求和的方法，这是数学学习中数学思想方法的体现，这是一种弱抽象.只是与等差数列求和具有相似的形式，但是否有一定的道理，教师应该利用此契机深入引导学生探究.

数学抽象思维与学生的情感和个性特征有密切联系，要培养数学抽象思维能力必须充分调动学生的主动性和创造性.在教学中，我们采用多种形式，让学生的思想在生动活泼的气氛中得到锻炼和发展，并培养他们的意志品质.对于有新意、思想深刻的学生则给以鼓励，促使他们积极奋发、更有兴趣学习；对于后进生也要注意保护他们的积极性，肯定他们的一得之见.

高中数学核心素养的思维价值

相关推荐