决策树有ID3,C4.5和C5.0等多种划分方法,是一种树状划分状态,在每一个节点进行条件的判断,按照一定的划分标准最终生成决策结果,其目的是为了解决机器学习中的多分类问题,本节采用信息增益最大化来进行树的划分。决策树的训练集中训练得分为0.968,测试集中测试得分为0.767。图5.13决策树调参训练过程当节点的Gini指标小于等于某个阈值时,则表示该节点不需要进一步拆分,否则需要生成新的划分规则。......
2023-06-15
1.金融风险测度VaR简介
20世纪90年代后,一种卓有成效的新型风险度量方法——VaR方法在金融界得到广泛应用。
所谓VaR,即“Value at Risk”的缩写,中文通常译为风险价值(或险值、在险价值、风险值),指在给定的市场条件与置信水平下,某一金融资产或证券组合在给定的时间区间内的最大期望损失。作为一种利用概率论与数理统计来评价风险的方法,它能用非专业人士都能够理解的非技术术语对金融市场风险给出总括性评价,兼具科学性与简明易操作性。
摩根大通(JP.Morgan)对VaR的定义为:VaR是在既定头寸被冲销(be neu-traliged)或重估前,可能发生的市场价值最大损失的估计值。而Jorion则把VaR定义为:给定置信区间的一个持有期内的最坏的预期损失。
确切地说,VaR可表示为:
PrΔt(ΔP>VaR)=1-c (4-34)
式中,ΔP为证券组合在持有期Δt内的损失;c为风险测量的置信水平;VaR为此置信水平下处于风险中的价值。对于每一个给定的市场风险函数,我们都可针对需要的测量精度c计算出相应的损失最大值VaR,用它直观地表示风险大小。图4.13是VaR的概念简图。
VaR之所以具有吸引力,是因为它把金融机构的全部资产组合风险概括为一个简单的数字,并能以指定的货币计量单位来表示风险管理的核心——潜在亏损。VaR实际上是要回答在概率给定情况下,金融机构投资组合价值在下一阶段最多可能损失多少。
VaR具有以下特点:
1)用来简单明了地表示市场风险的大小,单位是美元或其他货币,没有任何技术色彩和专业背景的投资者和管理者都可通过VaR值对金融风险进行评判。
2)可以事前计算风险,而以往风险管理的方法都是在事后衡量风险大小。
3)不仅能计算单个金融工具的风险,还能计算由多个金融工具组成的投资组合风险,这是传统金融风险管理所不能做到的。
4)VaR的最大优点在于测量的综合性,可以将不同市场因子,不同市场的风险集成为一个数,较准确地测量由不同风险来源及其相互作用产生的潜在损失,较好地适应了金融市场发展的动态性、复杂性和全球化趋势。

图4.13VaR概念简图
2.VaR的计算方法概述
VaR的计算方法通常有三种:①历史模拟法;②参数法;③蒙特卡罗(Monte Karlo)模拟法。
历史模拟法是最简单的VaR计算方法。其核心在于根据市场因子的历史样本变化模拟证券组合的未来损益分布,利用分位数给出一定置信度下的VaR估计,即利用历史实际发生的回报值时间序列{yt-j}t-1j=1的经验分布,计算一定置信水平α下的VaR。
利用历史模拟法的非参数性,可以通过样本数据体现回报分布的形状,而不需要事先假定样本数据的特定分布形式,也无需估计分布参数,因此非常适合实际回报偏离正态分布的情况。但实际应用中存在的主要问题是,如果历史样本抽样区间太短,则会导致VaR估计不精确,增大样本区间又会导致市场因子的波动性偏低,可能违反独立同分布假设,因此估计精度难以确定。
参数分析法是最常用的VaR计算方法。利用证券组合的价值函数与市场因子的近似关系,市场因子统计分布(方差-协方差矩阵)可简化VaR计算。
由于只需要利用一阶或二阶泰勒展开式近似估计组合价值,参数分析法大大简化了VaR计算,风险管理研究人员广泛利用此法推导出很多衍生模型。但其对分布的正态性假定往往与实际不符,导致模型估计精度不够。
蒙特卡罗模拟VaR方法亦称随机模拟方法(Stochastic simulation),是最有前途的VaR方法。其思想是建立一个概率模型或随机过程,使它的参数等于问题的解,然后通过对模型或过程的观察计算所求参数的统计特征,最后给出所求问题的近似值,解的精度可用估计值的标准误差表示。
基于蒙特卡罗模拟的VaR计算,主要是重复模拟金融变量的随机过程,使模拟值包括大部分市场因子的变化情况,模拟得出组合价值的整体分布情况,在此基础上可求出VaR,具体分为以下三步:
1)情景产生。选择市场因子变化的随机过程和分布,估计其中相应的参数,模拟市场因子的变化路径,建立市场因子未来变化的情景。
2)组合估值。对市场因子的每个情景,利用定价公式或其他方法计算组合的价值及变化。
3)估计VaR。根据组合价值变化分布的模拟结果计算特定置信度下的VaR。
蒙特卡罗模拟方法的优点是属于全值估计,可以处理非线性,大幅波动及厚尾问题,可以模拟回报的不同行为(如白噪声、自回归和双线性等)和不同分布。缺点在于计算量大,且依赖于特定的随机过程和所选择的历史数据,产生的数据序列是静态的伪随机数,具有模型风险。随机数中存在的群聚效应会浪费大量观测值,降低了模拟效率。
综上所述,经典VaR的三种计算方法,在基本原理和计算思路上都有很大差异,因此计算方法的选择标准不仅是估计的准确性,更多的取决于风险经理对风险测量过程不同因素的偏好组合。因此,只有明确了各种方法应用时的优缺点,才能针对不同的资产组合选用或混合使用不同方法。
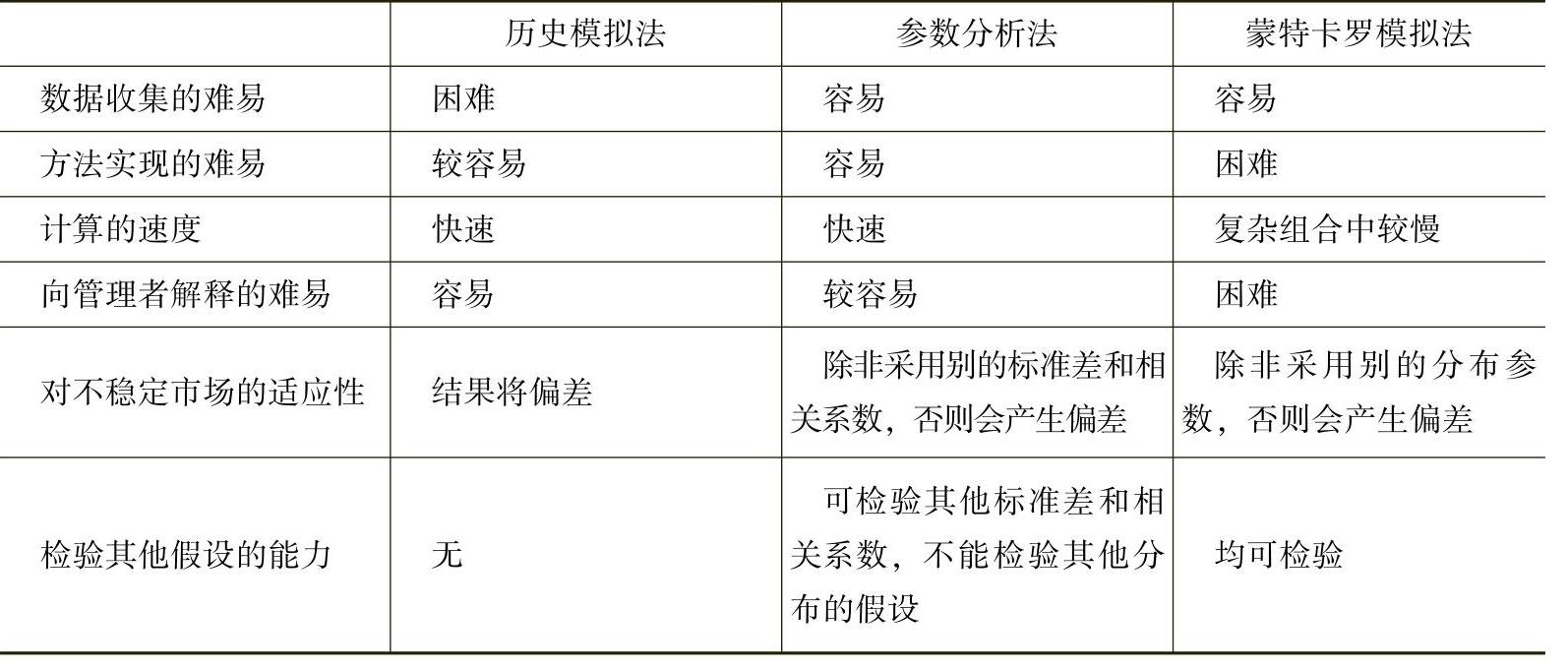
作为总结,表4.12比较了三种经典VaR计算方法应用于实践时的效率。
表4.12 VaR计算方法比较
3.VaR与可信性等级
除去时间的影响,金融学上VaR的含义与M&S可信性评估定义中R的含义一致。从式(4-32)、式(4-33)、式(4-34)和图4.11、图4.12中可以看出这一点,只不过此时的风险函数是F(D,ξ)。此后通常称M&S可信性评估值R为VaR,因此对于M&S的评估用一个三元组(D,VaR,β)来表示。
假设策略S1、S2的评估结果为(D1,VaR1,β1)、(D2,VaR2,β2),则:
1)β1=β2的情况下,若VaR1>VaR2,则S2<S1;若VaR1=VaR2,则S1=S2,反之亦然。
2)β1≠β2的情况下,S1、S2比较无意义。
由前所述,VaR值表征了模型(S,ξ)的总体风险,自然可以用VaR来表征M&S的可信性。
可信性是一个定性与定量相结合的概念,不能单纯指出某M&S是否可信,即可信性不是一个二值逻辑的概念,用语意值来表达更为贴切、自然。
按照人们评判事物的习惯及便于研究的目的,例如可将可信性分为五个等级,分别为非常可信、可信、一般、不大可信和不可信。计算VaR时通常取的置信水平有:90%、95%和99%。以置信水平95%(记为VaR0.95)为例,VaR值与可信性等级的对应关系设置见表4.13。
表4.13VaR0.95与可信性等级的对应关系

显然,置信水平越高,VaR越大,因此置信水平不同,可能导致得到的可信性等级评估结果不同。设置可信性等级与VaR的对应关系,需以M&S的应用目的为参照,由相关领域专家给出。同时,对于以什么层级的VaR值及多大的风险值来对应M&S可信性的各个等级,也需要领域专家结合实际给出,表4.13不过给出了一种参考。
4.M&S可信性评估之路
根据前文所述,可信性评估是在相关V&V活动完成后进行的,而V&V活动是在有限资源的限制下进行的。于是,实际选择的V&V策略是由相关V&V准则、当前资源约束和领域专家共同确定的。V&V策略一旦确定,那么根据该策略的V&V活动进行完毕后,根据模型(S,ξ),进行相应的风险分析,得到VaR。随后领域专家根据M&S的特质,制定相应的可信性等级标准表,对照VaR值和相应可信性等级标准表,不难得到对M&S可信性评估的语意值。图4.14简单明了地展现了M&S可信性评估之路。
5.M&S可信性评估之实例分析
进行可信性分析的前提条件是知道V&V的策略。下面以SCCPM对问题2求解得到的最后策略(附录F)为例,进行相应的可信性分析,假设置信水平为β=0.90,而可信性等级的划分标准见表4.13。
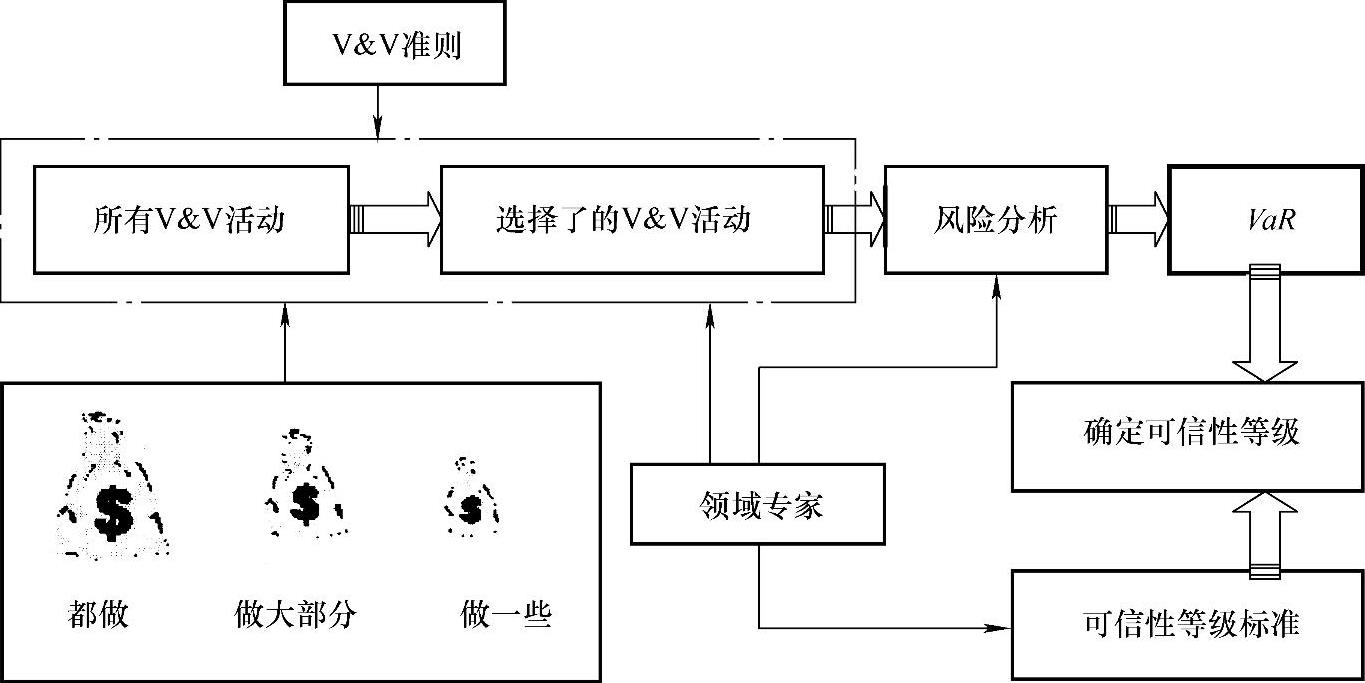
图4.14 M&S可信性评估之路
为求解三元组(D,VaR,β),随机模拟3000次,得到VaR0.95=180.6192K元,而极限风险值R0=1094.72K元。因此,有VaR0.95/R0=0.1650,根据表4.13,依照该策略进行V&V后,该M&S预期的可信性等级是“一般”。图4.15给出了3000次模拟中,M&S风险分布的直方图和概率密度曲线。
其实,表4.13所制定的可信性等级的划分标准是非常高的。如果完全可信的条件是VaR0.95≤5%R0,则在实际中很难达到,可以考虑将评估等级的上限5%改为10%或15%,下面的等级标准再依此类推。当然,对于有些M&S可信性等级的标准就是要高,例如置信水平可能需要0.99。总而言之,可信性等级标准的制定需要视情而动,应以M&S的应用目的为参照,由相关领域专家结合实际给出。

图4.15 M&S风险分布的直方图和概率密度曲线图
结合前文所述,M&S的V&V一般方法实施所涉及到的步骤、活动、参与人员、具体方法及相应结果见表4.14。
表4.14 V&V一般方法流程表
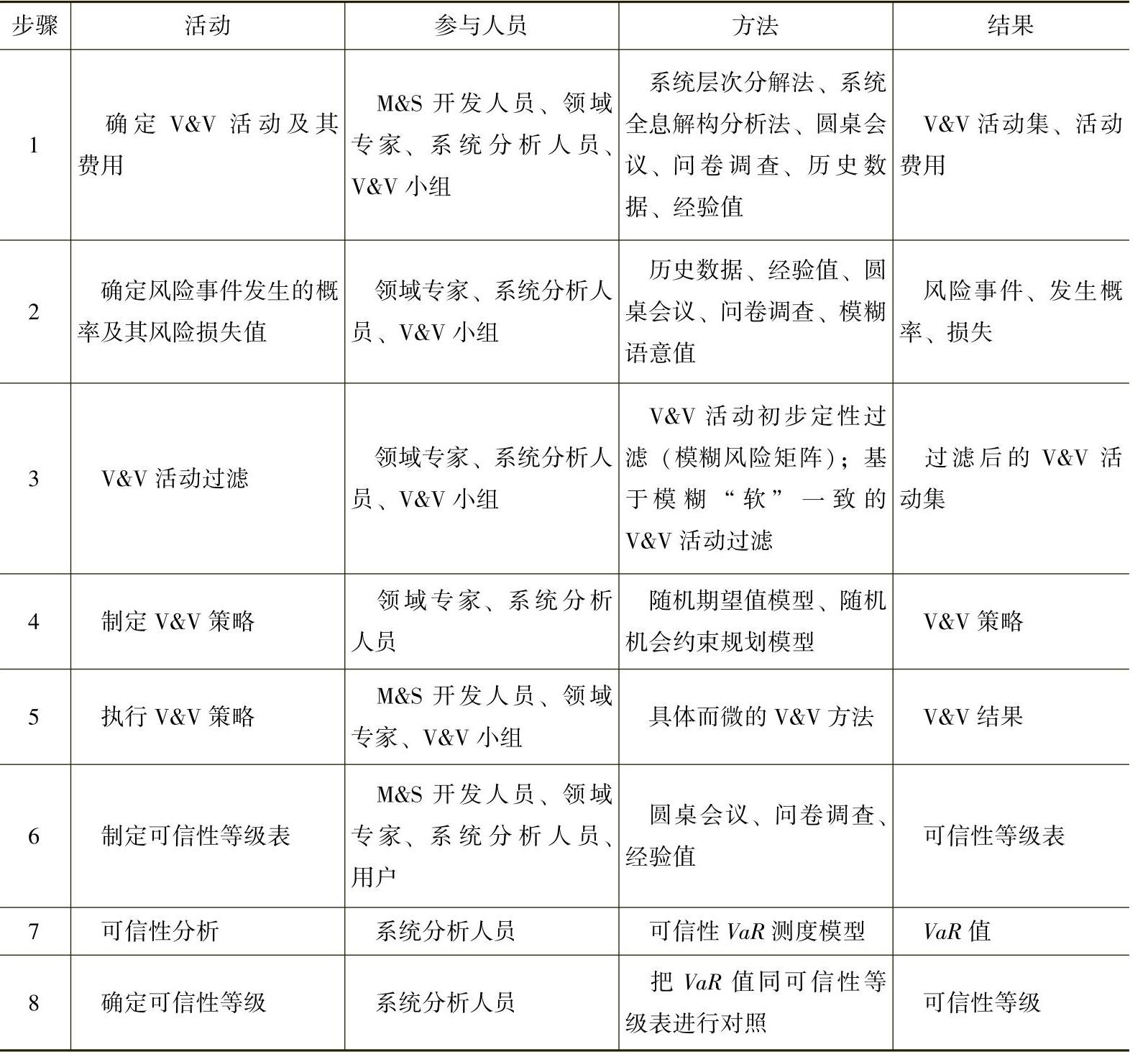
注:如果步骤8的可信性等级不符合要求,则返回步骤1。
[2]“中吾矩者,谓之方,不中吾矩者,谓之不方。是以方与不方,皆可得而知之。此其故何?则方法明也。”
[3]E[﹒]表示随机变量的期望值算子。
[4]这里的清晰完备是在当前SMEs所认识的相关知识范围之内,是相对概念。当然,在当前SEMs科学共同体的认识范围内,我们有理由认为V&V活动是清晰完备的。
[5]实践中,可以应具体问题,制定不同的风险矩阵表。

决策树有ID3,C4.5和C5.0等多种划分方法,是一种树状划分状态,在每一个节点进行条件的判断,按照一定的划分标准最终生成决策结果,其目的是为了解决机器学习中的多分类问题,本节采用信息增益最大化来进行树的划分。决策树的训练集中训练得分为0.968,测试集中测试得分为0.767。图5.13决策树调参训练过程当节点的Gini指标小于等于某个阈值时,则表示该节点不需要进一步拆分,否则需要生成新的划分规则。......
2023-06-15

COPA方法是基于癌症组样本数据的第r分位数来确定差异基因表达值的。OS方法计算OS*i统计量,并且引入启发式规则附加表达值,利用分位数的知识对基因芯片数据进行基因表达的差异表达基因检测。在式中,差异表达基因的数量默认为个。COPA方法、OS方法、ORT方法和MOST方法的共同特点是以参数方法,采用样本基因表达强度的中值和中值绝对离差定义差异基因表达的统计量,都利用基因表达的分位数检测差异基因表达。......
2023-11-21

Hu在2008年提出了LRS方法,LRS方法是基于似然性方法在基因表达谱数据中寻找癌症组样本基因表达强度的改变点,识别有差异表达的癌症基因,选取最大似然率进行癌症组样本检测。,n时,xij表示癌症组样本的基因表达强度。采用函数v=,其中Φ表示标准正态分布函数,对于0≤m0<m1<n和b>0,则有直接将LRS方法应用在相反的情况下,检测癌症组样本中过低调节的差异基因表达值。......
2023-11-21

1)资源量计算体积法是一种简单快速的页岩气资源评价方法,也是勘探开发程度较低区域进行页岩气资源量评价的基本方法,也是本文采用的计算资源量方法。表6.22渝东南地区五峰—龙马溪组页岩气资源量计算表......
2023-06-24

根据V&V原则,完全彻底的V&V是不可能的。虽然DOD VV&A RPG提供了几十种可供选择的V&V技术方法,但多会因经费和时间的约束而不能进行,这样测试模型和仿真的准确性必然受到影响。从产品质量的角度出发,准确性只是M&S质量的衡量标准之一,而确认准确性以外的任何一个质量特性,都能提高我们对于应用M&S的自信。软件工程中的SQA程序及TQM的思想为我们把VV&A从以“Accuracy-Centered”的评估转向以“Quality-Centered”的评估提供了大量指导。......
2023-08-15

正确度是检测结果与真值或接受参考值之间的一致程度。正确度试验的目的是度量和评价系统误差分量,即偏倚。正确度评价方法包括分析有证参考物质、方法比对、分析具有溯源性的参考物质和参加能力验证计划来获得正确度的结果,同时还可以结合回收率的考察结果评价正确度[8]。在这种情况下,100%的回收率并不一定意味着好的正确度,但差的回收率则一定意味着有偏倚。......
2023-06-29

3D CNNs模型在两种条件下的训练收敛速度如图5.5 所示,对比实验结果见表5.3。使用3D CNNs 模型在SBU-Interaction 数据集上进行动作识别可获得96.76%的平均识别率,通过迁移学习动作识别率可提高到97.42%,充分验证迁移学习在3D CNNs 模型上的可行性和有效性。......
2023-10-28

对于版权评估目前所常见的方法主要有重置成本法、现行市价法和收益现值法。重置成本法常用于资产评估之中,但用于版权评估中则有一定的难度。此外,造成版权的费用往往不与评估值相对应。现行市价法是通过对市场上可对比资产交换价格分析,来对资产评估值进行确定。......
2023-10-20
相关推荐