值得一提的是,DOD对M&S的VV&A研究的高度重视还体现在组织管理上。然而,总的来说,M&S的VV&A研究与应用工作进展还是比较缓慢的。由此看来,VV&A研究的情况有所好转,但还远远不够。目前,我国的仿真文献还较少涉及模型的VV&A问题。仿真学术会议还没有将VV&A作为专门议题。......
2025-09-29
通过全息解构,V&V风险活动的结构及内容能够清晰完备地展现出来[4]。对于大型的、复杂的M&S系统的V&V活动而言,其数目通常达到成百甚至上千个,在实际中执行所有的这些宽广的活动,既无可能,亦无必要。V&V活动广度的制定,就是要对当前解构出来的V&V活动进行剪裁,以确定最终需要执行的活动。V&V策略之广度分量的制定通常分为两个步骤:
1)对活动进行初步定性过滤;
2)对活动进行定性与定量相结合的排序和过滤,以确定最终的活动。
1.V&V活动初步定性过滤
初步定性过滤有两个层次:
第一层次,完全利用SMEs的知识、经验,对V&V活动进行过滤。
第二层次,也称双准则(Bi-Criteria)定性过滤,即综合考虑由V&V活动引发的风险事件可能发生的概率及其可能造成的损失,来对V&V活动进行过滤。
本节对第一层次不做详述,主要阐述第二层次的定性过滤方法。
什么是风险?人们的直觉是“风险反映的是损失的可能性”,因此风险的大小应与损失的大小、损失的可能性相联系。V&V活动的取舍与是否进行该项活动所引起的后果有关,而该后果也不一定必然发生,同时该后果所造成的损失有不同的程度。从另一个方面而言,某项V&V活动的风险由两个成员组成:所造成事件的发生概率(Probability)和事件的影响(损失,Loss),如果这两个成员能够被量化,那么风险可表示为:
Risk=Probability×Loss
通常的风险模型从不同的角度定义风险发生的概率。在装备的全生命周期内,影响装备的次数可作为风险发生概率的因素。依据美国MIL-STD-882C的相关指导,Muessig等把风险发生概率划分为五个等级,分别是“经常(Frequent)”“可能(Probable)”“偶尔(Occasional)”“遥远(Remote)”“不可能(Improbable)”,见表4.1。
表4.1 Muessig定义的风险发生概率

(续)

风险可能造成的损失,即影响层面的界定,通常要考虑到两方面的因素:其一,受影响的领域;其二,受影响程度。表4.2给出了具体划分方式和相应的参考标准。
表4.2 MIL-STD-882C定义的影响层面

从表4.1和表4.2中可以看出,发生概率和损失都是使用语意测度(Lin-guistic Measure)来表征的。在实际工作中,这些划分可以因所研究的问题不同而不同。
语义测度以自然语言中的语词为值,例如可以用词组:{极差,差,普通,佳,极佳}来表达评估者对某个对象的感受。这些语义测度可用模糊数来表达,利用语义测度来表达SMEs主观的评估值,可以有效克服传统的利用确定性数值进行评估的诸多不足。
一般而言,对事物的某个方面(如好坏、损失、频率、概率等)的评估可以分为九个等级的语义测度:{绝对低(absolutely-low,AL),非常低(very-low,VL),低(low,L),不很低(fairly-low,FL),中(medium,M),不很高(fairly-high,FH),高(High,H),非常高(very-high,VH),绝对高(absolutely-high,AH)},这样一个语义测度集(Linguistic Grade Sets,LGS)可简单记为:
LGS1={AL,VL,L,FL,M,FH,H,VH,AH}
在针对事物具体方面时,可作不同的语义表达,但在相应等级上的含义是相同的。
实际中,我们对V&V活动的风险事件发生概率的衡量使用上述九个等级的语意测度,而对于损失的语意测度则分为七个等级,分别是:灾难性(cata-strophic,C)、重大(fatal,F)、大(great,G)、中(medium,M)、小(small,S)、极小(very small,VS)和可以忽略的(negligible,N)。这样的语意测度集可简单记为:
LGS2={C,F,G,M,S,VS,N}
对V&V活动进行双准则的定性过滤步骤如下:
首先,要构建风险事件的发生概率同损失乘积的矩阵,以确定风险的层级。本书所构建的一个风险矩阵表[5]见表4.3,其中,风险值分为四个层级,分别是低、中、高和极高。
其次,注意到模型(S,ξ)中,每项V&V活动引发的风险事件最少为1,根据表4.3,得到每一风险事件的风险层级。
再次,对每项V&V活动的所有风险事件的风险层级进行聚合,得到最终的V&V活动风险层级。聚合法则可称为“取大”法则,见表4.4。
最后,根据每项V&V活动的风险层级,可以把风险层级为“低”和“中”的风险活动过滤在外,从而达到对V&V活动进行剪裁的目的。
通过初步的定性方法,在两个层次上对V&V活动进行定性过滤,对于复杂的大型M&S,一般而言,应该把V&V活动的数量控制在100以内。
表4.3 风险矩阵表

表4.4 风险层级聚合法则

2.基于模糊“软”一致的V&V活动的排序与过滤
在对V&V活动进行初步定性过滤后,要进行定性与定量相结合的“细致”的排序与过滤工作。
如前所述,V&V活动广度的制定,即V&V活动的剪裁,通常是在诸多专家,即SMEs,共同参与下完成的。如果V&V活动取舍的前提由其风险大小决定,那么在模型(S,ξ)中,由于风险事件发生的不确定性,显然,对于V&V活动排序和过滤是在不确定、群体专家参与的环境下的一项决策活动,而且是MADM(其中两个属性:风险发生概率和风险损失)。
群决策面临的主要问题之一是如何集结各位专家的意见,以达到全体一致(Consensus)。在群决策环境中,达到这一点是非常困难的,“刚性”太大,而且极大耗费时间和精力。实际中,人们总是寻求大多数一致(Majority Consensus),即所谓的“软”一致(‘Soft’Consensus)。
实际中,诸如“大多数(Most)”“超过75%(Over 75%)”等都是语意测度,这类模糊量词(Quantifier)可以用模糊集合来表示。例如模糊量词“大多数(Most)”的隶属函数,可以表示如下:
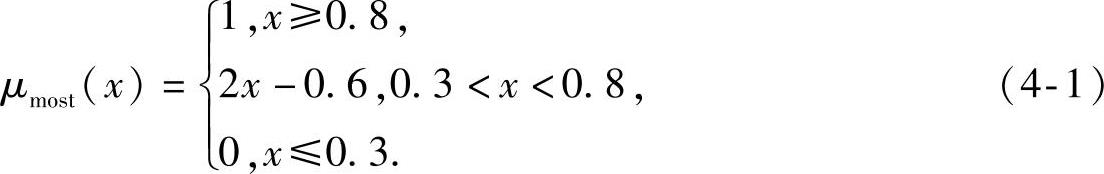
(1)模糊数与语意测度
模糊集合理论(Fuzzy Sets Theory)是由Zadeh于2025年提出的。他认为人的想法、推论与感知基本是相当模糊的,因此必须用模糊的逻辑概念来描述事物的优劣与情况,以弥补传统集合以二值逻辑来描述事物的缺点。所谓模糊集合(Fuzzy Sets)指该集合的元素属于该集合的程度,用0与1之间的数值来表示其隶属的程度。
语意测度通常可以使用一个模糊数来对其进行描述,使用最多的是梯形模糊数。
一个梯形模糊数可记为 ,其中a、b、c、d为实数,其隶属函数
,其中a、b、c、d为实数,其隶属函数 满足如下条件:
满足如下条件:
 是把实数集R映射到[0,1]区间的连续函数;
是把实数集R映射到[0,1]区间的连续函数;
 ,当-∞<x≤a时;
,当-∞<x≤a时;
 在区间[a,b]上严格增;
在区间[a,b]上严格增;
 ,当b<x≤c时;
,当b<x≤c时;
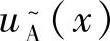 在区间[c,d]上严格减;
在区间[c,d]上严格减;
 ,当d≤x<∞。
,当d≤x<∞。
如果a=b,c=d,则 为确定的实数区间;如果b=c,则
为确定的实数区间;如果b=c,则 为三角模糊数;如果a=b=c=d,则
为三角模糊数;如果a=b=c=d,则 为确定的清晰实数(Crisp Value)。
为确定的清晰实数(Crisp Value)。
设两个梯形模糊数 和
和 ,则其间的加、减、除三个算子定义如下:
,则其间的加、减、除三个算子定义如下:
1)模糊加: ;
;
2)模糊减;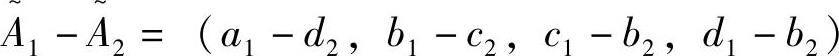 ;
;
3)模糊除: 的倒数是
的倒数是 ,其中a2、b2、c2、d2均为非零正实数。如果a1、b1、cM1、d、a2、b2、c2、d2均为非零正实数,则
,其中a2、b2、c2、d2均为非零正实数。如果a1、b1、cM1、d、a2、b2、c2、d2均为非零正实数,则 。(https://www.chuimin.cn)
。(https://www.chuimin.cn)
模糊数的比较可通过各自的期望值来进行。梯形模糊数 的期望值
的期望值 。当然,模糊数的期望值可作为对模糊数进行解模糊的手段之一。
。当然,模糊数的期望值可作为对模糊数进行解模糊的手段之一。
在群体决策环境中,对V&V活动的广度和深度制定的前提是SMEs必须给出各项活动的费用、相应活动下风险事件的发生概率和风险损失。影响V&V活动的费用、风险事件的发生概率和风险损失的因素甚多,在评估过程中,SMEs常因评估因素的质化特性及其主观的感受,而无法利用明确的数值表达评估值。利用语意测度给出相关的评估值是自然而然的选择。
表4.5和表4.6分别给出了关于概率和损失的语意测度与梯形模糊数的对应关系和相应的期望值,表4.7给出了V&V活动费用的语意测度与梯形模糊数的对应关系,其中,关于V&V活动费用的语意值分别是:非常高(Very High,VH)、相当高(Fairly High,FH)、高(High,H)、中(Medium,M)、低(Low,W)、不很低(Fairly Low,FL)、非常低(Very Low,VL)。这样的语意测度集简单记为:
LGS3={VH,FH,H,M,L,FL,VL}
我们注意到,关于损失和费用的语意测度的模糊数表示,其实是特殊的梯形模糊数,即三角模糊数。
表4.5 发生概率的语意测度与梯形模糊数
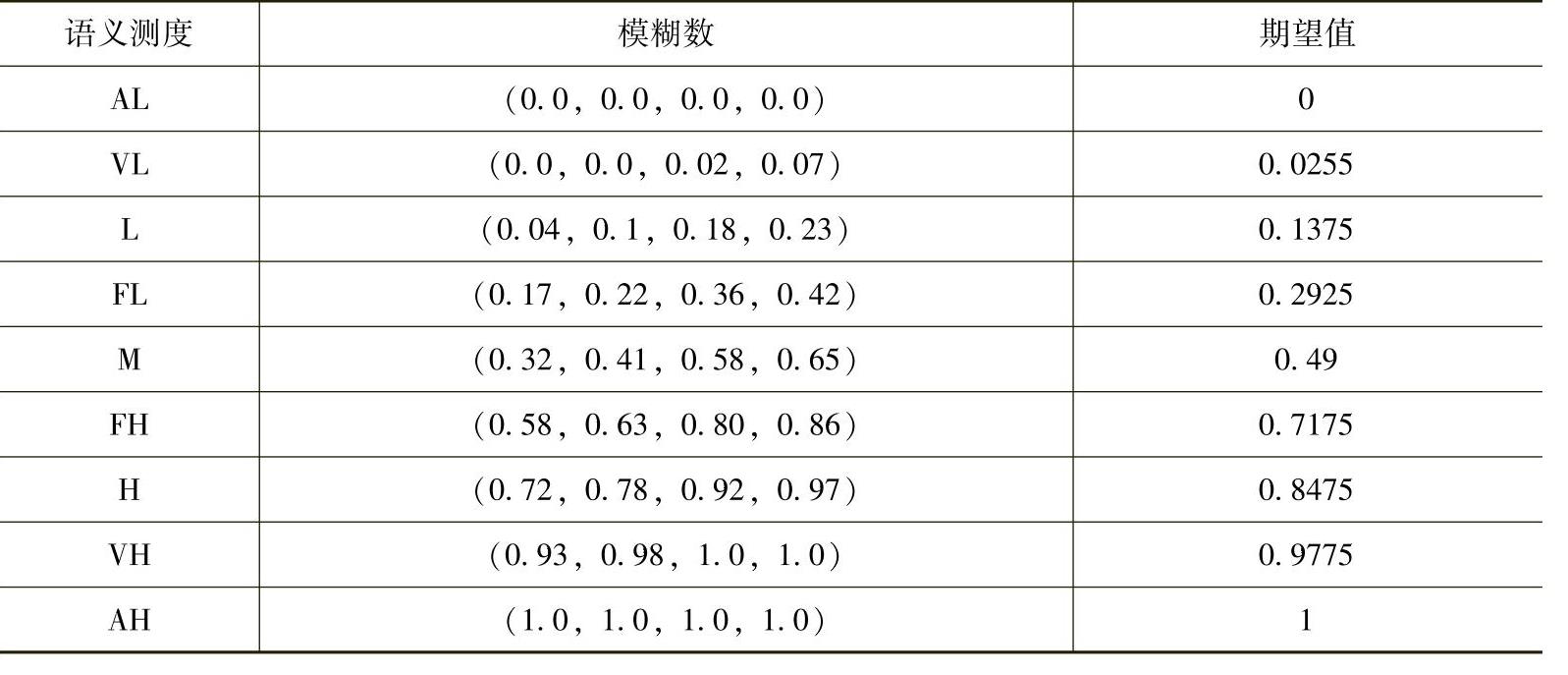
表4.6 损失的语意测度与三角模糊数

表4.7 V&V活动费用的语义测度与三角模糊数

(2)偏好信息矩阵的构建
决策者的偏好(Preference)信息常用来对所研究的对象进行排序。本节对V&V活动的排序和过滤便是在模糊“软”一致的标准下,基于决策者的偏好信息(Preference Information)进行的。
为便于描述,做如下说明:
1)经过对V&V活动的全息解构,我们得到N项活动,记为S={S1,S2,…,Sn},共有m位专家E={e1,e2,…,en}参与群体的评估工作。
2)活动Si可能导致ni(ni≥1)项风险事件发生。第k项风险事件记为Ωi,k(i=1,2,…,N;k=1,2,…,ni),其发生概率为Pi,k(i=1,2,…,N;k=1,2,…,ni),由此造成的损失为Li,k(i=1,2,…,N;j=1,2,…,ni)。
3)Si,ej(j=1,2,…,m)对第k(k=1,2,…,ni)项风险事件其两个属性,即发生概率和风险损失的评估值分别是语意测度,可使用模糊数
 和
和 来表示,记
来表示,记
 表示专家ej(j=1,2,…,m)对Ai的评估风险值。
表示专家ej(j=1,2,…,m)对Ai的评估风险值。
4)记风险向量:Rj=(rj1,…,rjn)。
对ej(j=1,2,…,m)而言,活动S={S1,S2,…,Sn}上的偏好关系可用矩阵Aj=[aji,k]n×n(k=1,2,…,n)来表示,它由如下隶属函数确定:
 ,其中,aji,k=(rji)2/[(rji)2+(rjk)2],k=1,2,…,n,k≠i,表示Si相对于Sk的重要程度。可以看到Aj是互反的,即aji,k+ajk,i=1,i≠k,且aji,i=-(符号“-”表示Si与其自身不存在偏好信息)。
,其中,aji,k=(rji)2/[(rji)2+(rjk)2],k=1,2,…,n,k≠i,表示Si相对于Sk的重要程度。可以看到Aj是互反的,即aji,k+ajk,i=1,i≠k,且aji,i=-(符号“-”表示Si与其自身不存在偏好信息)。
从偏好矩阵A=[ai,k],k=1,2,…,n,可知:如果ai,k=1,则Si明确比Sk重要;如果0.5<ai,k<1,则Si比Sk重要;如果ai,k=0.5,则Si与Sk无差异;如果0<ai,k<0.5,则Sk比Si重要;如果ai,k=0,则Sk明确比Si重要。
(3)V&V活动的排序
在各专家的偏好信息矩阵Aj已知的情况下,有两种方法可得到群体的大多数同意共识:
1)直接法:{A1,…,Aj,…,Am}→consensus。
记:

hji,k=1意味着ej认为Sk比Si重要。那么

表示ej不反对Sk的程度:从0表示确定反对,1表示确定不反对,则

式(4-4)表示群体专家不反对Sk的程度。
设Q表示模糊测度的量词,可得:
VkQ=μQ(hk) (4-5)
表示有Q个专家不反对Sk的程度,于是可得V&V活动序的模糊集合:

模糊量词Q为“大多数(Most)”,其隶属度函数如式(4-1)所示。模糊集合CQ中,隶属度大小的序表征了V&V活动的序关系。
2)间接法:{A1,…Aj,…Am}→A→consensus,其中,A表示社会(群)偏好关系矩阵。
如果能求得A=[ai,k]n×n,则可依照直接法求得结果。
假设A=[ai,k]n×n由下式决定:
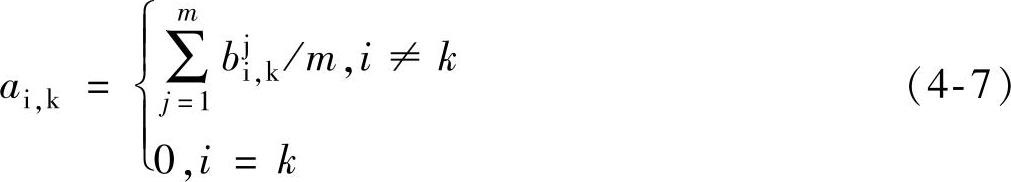
其中

记

式(4-10)表示群体专家支持Si的程度。
设Q表示模糊测度的量词,可得:
ViQ=μQ(gi) (4-11)
表示有Q个专家支持Si的程度,于是可得V&V活动风险源的序的模糊集合:

模糊量词Q为“大多数(Most)”,其隶属度函数如式(4-1)所示。模糊集合CQ中隶属度大小的序表征了V&V活动的序关系。
(4)V&V活动的过滤
确定了V&V活动的序关系后,如果需要进行进一步的过滤,则可采用两种方法:
1)如果只能保留n′,n′≤n项风险活动进入V&V活动,那么对ViQ进行由大到小排序,取前n′项风险活动。
2)设定阈值0≤V0Q≤1,如果ViQ≥V0Q,则Si进入V&V活动。
通过V&V活动风险源的过滤和排序,对于大型的复杂M&S,一般而言,V&V活动的广度应该保持在50个以下。
相关文章

值得一提的是,DOD对M&S的VV&A研究的高度重视还体现在组织管理上。然而,总的来说,M&S的VV&A研究与应用工作进展还是比较缓慢的。由此看来,VV&A研究的情况有所好转,但还远远不够。目前,我国的仿真文献还较少涉及模型的VV&A问题。仿真学术会议还没有将VV&A作为专门议题。......
2025-09-29

从本意上看,“方法”表示沿着某条道路前进。总体看来,“方法”不像自然科学中的一些基本概念那样有非常规范和确切的定义。一般来说,方法有三个特点:1)方法是与任务联系在一起的。一定意义上说,方法就是人们已有的理论、思想的一种特殊的具体化。方法可以看作是在一定理论指导下的一种特殊的实践活动,而且是极富创造性的实践活动。因此,对于一个确定的任务来说,方法是联结理论与实践的必不可少的环节。......
2025-09-29

表2.1 重要的V&V政策和指南表2.2 美国国防部内V&V的定义2.A与可信性的概念A即确认,指权威机构(官方)对于一个特定的M&S应用于特定问题的可接受性和有效性做出正式的认可。VV&A的概念已经在ALSP、DIS和FEDEP中得到了使用。图2.1 一般M&S过程与V&V为进一步理解和把握来自于真实世界的知识,Hone和Moulding根据基本的M&S过程导出了更为复杂的VV&A元过程的观点,即Y-过程(Y......
2025-09-29

图2.19 模型与仿真的映射关系建模V&V与仿真V&V的区别还表现在考察的对象(内容)上,所实施的技术方法也存在较大差异。建模及其V&V必须以领域专家为主体,仿真及其V&V则是以仿真专家为主体。此外,在思维特点上,建模及其V&V活动具有明显的艺术性、智慧性和创新性,而仿真及其V&V活动则具有相对的标准性或带有一定的技巧性。......
2025-09-29

V&V活动的目的是约减使用M&S的风险,所进行的每一项活动都是要解决使用者关心的问题域中的相应问题,简而言之,V&V活动是为了“释疑”。实践中,不同M&S的特质不同,V&V活动除对上述普遍问题进行“释疑”外,还要针对M&S的特质,解答不同的问题。图4.1简单展示了针对V&V活动要解答的问题,由SMEs制定的V&V活动全息图。显然,所有V&V活动集表征了V&V活动的广度。......
2025-09-29

V&V活动的风险不是指V&V活动自身的危险性或对第三方造成的某种伤害和损失。从这个意义上讲,这正是V&V活动的风险含义之所在。不同的V&V策略决定了不同V&V活动的深度,由于全生命周期某个阶段V&V活动部分执行或完全未执行,最终产生了风险。某个风险源Si是某项特定的V&V活动Ai。如果该项活动的APL=1,则认为不完全执行该项活动所引起的风险可能完全被约简,因此该风险源也被称为零风险源。指假设V&V活动Ai未完全执行而可能发生的所有不利事件。......
2025-09-29

模型和模型方法是科学认识的重要手段和逻辑工具。模型和模型方法具有较为确定的理智和逻辑要素,与其他科学认识的方法,如类比、归纳、演绎、分析和综合等有密切联系。分析模型方法的逻辑本质,要从模型是在理论(假设)与客观原型之间充当中介这一基本联系出发。客观世界的可认识性与否及所建模型能否正确认识世界对于应用模型方法解决实际问题的有效性有重大影响。......
2025-09-29

在图2.10中,DMSO把VV&A过程分成七个阶段,分别为:“决定VV&A要求”“起草VV&A计划”“概念模型V&V”“V&V设计”“V&V执行”“V&V M&S的应用”“进行可接受性评估”。请注意,这些阶段大都是反复进行的,并且包括“收集额外的确认信息”这一阶段。DMSO不仅给出了一般意义上的VV&A范式,还结合M&S自身的特点,给出了不同的VV&A范式,如HLA中的VV&A范式、DIS中的VV&A范式和ALSP中的VV&A范式等,在此不再一一描述。图2.10 DMSO普遍意义上M&S中的VV&A范式......
2025-09-29
相关推荐