后V&V评估方法-建模与仿真VV&A系统观

2023-08-15 理论教育版权反馈

【摘要】：后V&V阶段即V&V活动执行完毕的后续阶段。这一阶段的主要任务是对整个M&S的可信性进行评估。应用AHP对M&S可信性在功能层次水平上进行评估的文献有许多，如杨瑞平、商长安、柳世考和张伟等，特别是Osman Balci提出的一整套基于功能层次分解法的可信性评估方法值得研究和借鉴。AHP是基于功能层次分解法进行M&S可信性评估的核心方法，在此基础上，不排除在进行数据处理时采用模糊数学方法和灰色、粗糙理论等不确定推理方法。

后V&V阶段即V&V活动执行完毕的后续阶段。这一阶段的主要任务是对整个M&S的可信性进行评估。

可信性评估的方法在诸多文献中均有讨论，主要可分为三大类：功能层次分解法、相似理论法和证据理论法。

1.功能层次分解法

一个系统可定义为如下的集合结构：

S=＜T，X，Ω，Q，Y，δ，λ＞

式中，T是时间基；X是输入集；Ω是输入段集；Q是内部状态集；Y是输出集；δ是状态转移函数；λ是输出函数。

按照以上定义，系统还可描述为

S：XF→Y

式中，F为功能集；X、Y意义同上，即系统S在X的作用下经过F处理后得到Y。单纯用X、Y来描述系统，系统是在行为水平上的仿真；单纯用F来描述系统，系统是在状态结构水平上的仿真；同时用X、Y、F三者描述系统，则系统是在分解结构水平上的仿真。系统模型可在分解结构水平上描述系统功能，是功能性层次分解的依据所在。

在这一水平上描述系统，将系统看作由许多子模块相互联结而成的一个整体，如图2.15所示。

需要指出的是，功能层次分解法是建立在模型的结构可分解和在分解时将模型模块功能化这两点之上的。

AHP是一种先把复杂系统中各因素构造为一个多层次的结构模型再进行分析的方法。应用AHP对M&S可信性在功能层次水平上进行评估的文献有许多，如杨瑞平、商长安、柳世考和张伟等，特别是Osman Balci提出的一整套基于功能层次分解法的可信性评估方法值得研究和借鉴。

AHP是基于功能层次分解法进行M&S可信性评估的核心方法，在此基础上，不排除在进行数据处理时采用模糊数学方法和灰色、粗糙理论等不确定推理方法。

2.相似理论法

（1）相似理论的基本原理

相似理论的基本原理包括同序结构原理、信息原理和支配原理等。这些原理反映了相似系统的形成和演变规律。相似理论用于M&S的可信性评估是因为相似理论认为，M&S本质上就是依据相似原理人为地建立某种形式的相似模型去模拟实际系统。

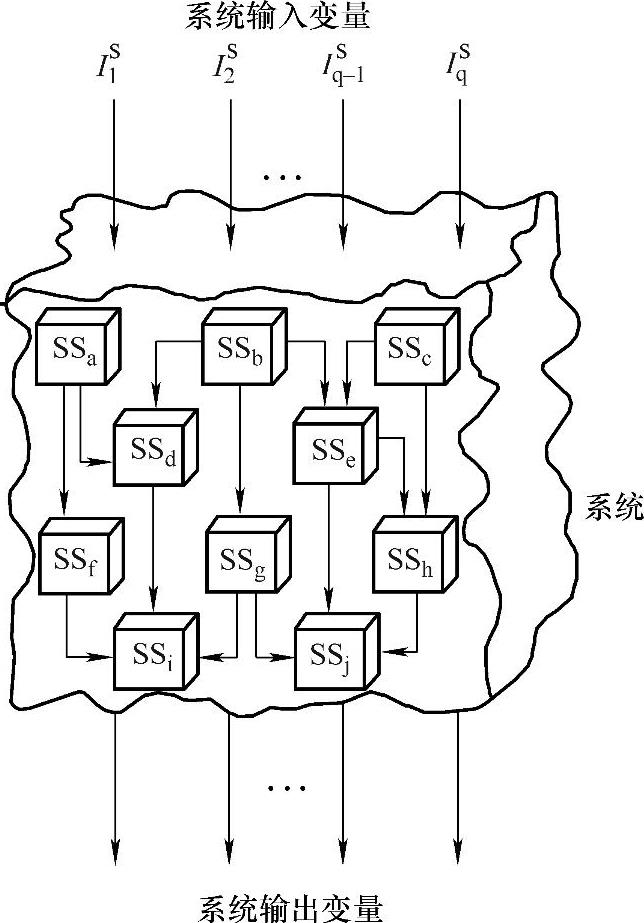
图2.15 系统的分解结构

系统内部要素间相互联系的方式和相互作用的顺序为系统序结构。相似理论的同序结构原理认为，任何系统都有一定的序结构，序结构的规律性形成有序结构，其中包括空间有序、时间有序和功能有序。系统的序结构决定了系统的整体特性。当系统序结构存在共同性时，系统之间存在相似性，其相似程度取决于系统序结构的共同性程度。基于系统相似性的仿真模型应以某种形式、在某种程度上反映实际系统的空间序结构、时间序结构和功能序结构的规律性。具体来说，空间有序表征系统组成要素的空间排列、组合和联系方式的规律性。时间有序表征系统要素随时间变化的运动规律。功能有序表征系统要素在相互作用过程中所表现出的各种功能发挥秩序的规律性。建模的过程描述了系统的序结构。因此，仿真模型与实际系统就具备了序结构上的相似性。

相似理论的信息原理认为，系统序结构的形成和演化与系统的信息作用相关。不同系统间的信息作用存在共同性时，系统间形成相似性。信息作用的内容、形式和信息场强度及其分布规律越接近，系统间的特性越相似。基于系统相似性的仿真模型应反映系统的信息流规律，包括信息作用的内容、形式和信息场强度及其分布规律。分析系统的信息流主要是系统同外界进行交换的输入、输出信息。

相似理论的支配原理认为，受相同自然规律支配的系统间存在一定的相似性。系统相似程度的大小取决于支配系统的自然规律的接近程度。基于系统相似性的仿真模型应能反映支配实际系统的自然规律。因此，应研究这些自然规律，并以某种形式体现在仿真模型中。据此建立的仿真模型反映了不同系统的相同动态变化过程。

如前所述，相似理论认为，模型是依据相似原理人为建立的某种形式的系统替代物，它应能在某种程度上反映实际系统的序结构、信息作用关系和自然支配规律。模型与实际系统之间的相似性是客观存在的，只是在相似形式和相似程度上有所区别。采用何种相似形式取决于建模与仿真的特定应用，只能在一定的相似形式下讨论模型与实际系统相似程度的大小。因此，可以把相似度作为仿真可信性的客观标准和定量指标。如果定义相似度S为模型与实际系统之间的相似度，则有S∈[0，1]。定义可信性为C，则C与S的大小成正比，即C∝S。

由图2.16中可知，通过分析模型同实际系统在输入、输出（相似性的信息原理）和结构水平上（相似性的同序结构原理）的相似性来对模型同实际系统的相似度进行量化分析，从而实现对模型验证的量化研究不失为一个好方法。在进行模型同实际系统的相似性分析时，模型被看作是同实际系统相对的另一个系统，实际系统一般称为原型（系统），对实际系统的相似简化称为模型（系统）。

图2.16原型与模型的相似

（2）相似元和相似度的度量

系统是由不同要素或子系统组成的，不同系统的组成要素不尽相同，相似元指系统间具有共同属性和特征的组成要素所构成的单元。当系统A中要素a_i与系统B中要素b_j为对应的相似要素时，用相似元描述，记为u_ij（a_i，b_j）。如果系统间有n个相似元，用u₁，u₂，…，u_n表示，记为U={u₁，u₂，…，u_n}。我们知道，组成每个系统的每个要素都可能有多个特征，现在考察系统间某个相似元，设该相似元有m个共有特征，记为s₁，s₂，…，s_m，记u_j（a_i）为要素a_i相对于特征s_j的特征值，记u_j（b_j）为要素b_j相对于特征s_j的特征值，则要素a_i、b_j相对于特征s_j的特征值比例系数记为

相似度是系统间相似要素的数量、相似元的数值及每个相似元对系统相似度的影响权系数等因素的函数。假设系统A由k个要素组成，系统B由l个要素组成，系统A、B间存在n个相似要素，构成n个相似元u₁，u₂，…，u_n，记为q（u_i）。每一相似元对相似系统相似程度的影响权重SMEs或采用AHP确定，记为β_i，且∑β_i=1，则相似系统的相似度可定义为

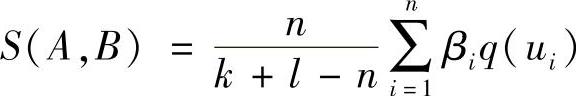
式中，

综上所述，系统间的相似度可表示为

S（A，B）=α_sS_s（A，B）+α_InS_In（A，B）+α_OutS_Out（A，B）

式中，α_s、α_In、α_Out分别表示系统结构水平、输入、输出在相似度评估中所占的权重，可由相关SMEs同模型的发起者和使用者根据模型的特定应用目的来议定或采用AHP来确定。这三个参数满足归一化条件：α_s+α_In+α_Out=1。

3.Dempster-Shafer证据理论法

证据理论是Dempster在研究统计问题时首先提出的，Shafer把它推广到更为一般的情形。证据理论提出后，引起业界极大的兴趣，模糊数学创始人Zadeh和专家系统（MYCIN）的主要开发者之一Shortliffe，都积极地进行证据理论的理论模型解释、算法实现及其实际应用的研究。Dubois等人指出，证据理论中的信度函数是一种模糊测度，他们还以集合论的观点研究证据的并、交、补和包含等问题。Smets将信度函数推广到假设空间（识别框架）Θ的子集上，并提出了Pignistic概率和TBM。Pawlak提出粗糙集（Rough Set）理论为证据理论的发展提供了新的机制，它使无限框架上的证据理论向有限框架上的近似转化成为可能。

人们使用证据理论解决了许多领域的不确定信息的处理问题，证据理论同样也可为M&S的可信性评估提供新思路。

转换角度，可认为V&V活动是为M&S可信性的建立寻求证据支持的一个过程。每多进行一项V&V活动，便可认为在相应的问题域上M&S的可信性得到更多一项证据的支持。如果相对完备、完全地进行所有V&V活动，则M&S的可信性便得到相对完备、完全的证据支持，自然会获得更高的可信性。图2.17表示可信性由一系列准则支持，而每一个准则又有相应的论据支撑，每个论据又都通过相应的V&V活动获得相应的一系列证据来说明，由此形成了一个从最底层证据到最高层可信性的递阶层次结构。

由图2.17可知，最终可信性的确定是通过底层一系列证据的融合得到的。而这些证据在很大程度上是不确定的（不完备、不清晰、模糊等）信息。而证据理论为不确定信息的表达和合成提供了自然而强有力的方法，使它在很多领域中获得了广泛应用。

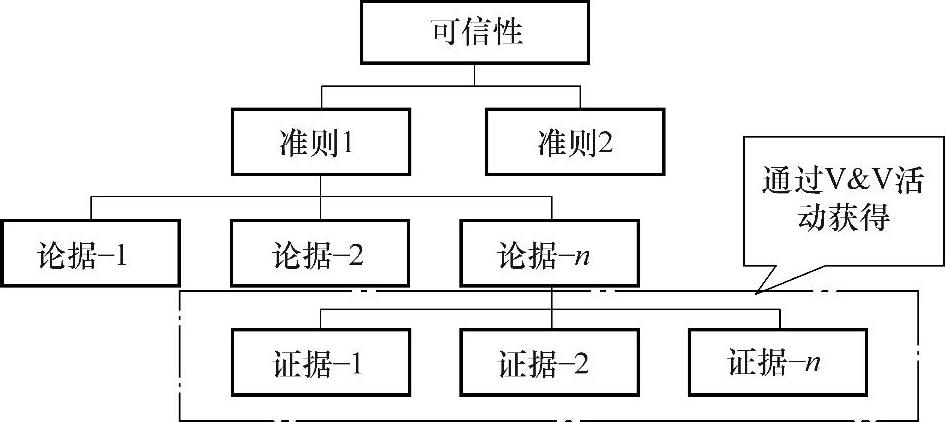
图2.17 从证据到可信性的层次结构图

设可信性识别框架集为Ω，来自不同证据源的信度分配函数为m_i，对属于识别框架集Ω的子集的A和B，可使用证据理论的合成法则：

除该法则外，还可使用TBM来对证据到可信性的结果进行聚合。

后V&V评估方法-建模与仿真VV&A系统观

相关推荐