数学教学论：优秀的教学途径

2023-08-13 理论教育版权反馈

【摘要】：作为教育形态的数学文化，必然要求如何进行数学文化的教学。数学文化的教学可以在课堂内外进行，其基本的前提条件是必须在教师的指导下进行。数学文化课外活动的形式是多种多样的。有的以学生写数学小论文的形式来进行，以充分发挥学生数学方面的聪明才智，增强学生的创新意识，提高学生发现问题和解决问题的能力。

作为教育形态的数学文化，必然要求如何进行数学文化的教学。现代教学论认为教学不仅仅是课堂教学，还引申到课堂外。数学文化的教学可以在课堂内外进行，其基本的前提条件是必须在教师的指导下进行。

（一）数学文化课外活动

课外活动包括课前活动和课后活动。课外活动围绕的主题是提高学生学习数学的兴趣，增强学生的数学应用意识，拓宽学生的数学视野，促成学生逐步形成正确的数学观。

数学文化课外活动的形式是多种多样的。有的以介绍数学家生平事迹为主要对象，记人也记事。数学家的故事让学生懂得数学家所取得的数学成就是数学家们不断进取、严谨治学的精神的过程，从而使学生获得精神力量。有的以介绍数学概念的发现、数学方法的发展、新的数学分支的发现等为内容，向学生阐明数学思想方法，提高学生对数学本质的认识。有的以数学问题的形式，通过数学游戏故事来体现出来，将数学原理融于娱乐之中。有的以数学讲座为形式，其内容非常广泛，可邀请一些数学家作讲演，也可以请本校老师来作讲座。还有以课外阅读的形式进行，以培养学生自学能力，但课外阅读材料必须适中，最好由教师提供参考书目，教师进行必要的阅读辅导，建议学生做好读书笔记，组织学生讨论，写读后感。有的以学生写数学小论文的形式来进行，以充分发挥学生数学方面的聪明才智，增强学生的创新意识，提高学生发现问题和解决问题的能力。

（二）数学文化的课堂教学

这是数学文化教学的主渠道，核心是将数学思想方法、数学文化的科学价值等融入一体，让学生在数学文化背景下，学习、体会数学。

（1）课堂教学注意与数学现实的联系。例如，在数学课程教学中，教师采取以下方法来认识圆锥曲线的性质。教师问“：一个半球面状的酒杯，内部半径为R的球，毫无疑问，球可坠到杯底。但若取一个内部为某圆锥曲线（抛物线、椭圆、双曲线）旋转面的酒杯，杯口足够大，小球何以能坠底？”^[8]学生们言论纷纷，但一时无以对答，教师又具体给出小球半径若等于圆锥面焦点到相应顶点的距离时，小球能坠底吗？经计算后、考虑后，有的同学说能，有的说不能。教师请几位同学说一说理由，说不能的同学举了抛物面的镜子，如旋成抛物面的抛物线方程为y2=2px（p＞0），若小球能坠入杯底，相应小球被抛物线的面截成的圆一定过抛物线顶点，圆的方程为（ pagenumber_ebook=226,pagenumber_book=213 ，即y2=-x2+px，代入y2=2px，得x2+px=0，方程有两实数根，故此时圆与抛物线交点不唯一，说明小球实际上不能坠底。而持相反观点的人说，旋成圆锥面的圆锥线中，由于曲线上任意一点到焦点的距离等于它到相应准线的距离与其离心率之积，可见曲线上的点以顶点距焦点最近，故当以顶点与焦点距离为半径的球放入酒杯一定能坠底。看来持两种观点的人都有各自的理由，谁的理由更充分呢？多数学生的立场还是模棱两可的。这时，教师叫大家观察方程x2+px=0的根：x=0，x=-p，发现根x=-p并不在方程y2=2px（p＞0）中的x的允许值范围内，说明圆与抛物线并无更多交点，因此可判断无论用什么方法，结论只有一个：此时的小球可坠到杯底。为了充分比对，教师又说明了椭球面酒杯的情形：由相应圆（x-c）2+y2=（a-c）2与椭圆方程 pagenumber_ebook=227,pagenumber_book=214 ＞b＞0），消去y得

虽然判别式 pagenumber_ebook=227,pagenumber_book=214 ，但两根x=a及x=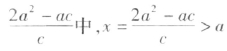，超过x的取值范围［-a，a］。类似相应圆、双曲线方程问题也有此情形。学生对此深信不疑，进而，可以知道：酒杯壁为抛物面时，球半径值在（］上时，杯壁为椭球面时小球半径值在（0，a-c］上，杯壁为双曲面（取相应双曲线方程为 pagenumber_ebook=227,pagenumber_book=214 时，小球半径值在（0，c-a］上，小球均可坠到杯底。

“那么，更一般地，小球半径在什么取值范围内，可坠到杯底？”学生们随后积极思考，除已有结论外，对于抛物面型的情形，学生取相应抛物线y2=2px（p＞0）、圆（，得x2x+2（p-a）x=0，解得x=0与x=2（a-p），可见，当时，小球可坠杯底，结合前面所求，适合条件的小球半径值的范围是（0，p］。

对于椭球面型的情形，取相应椭圆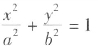 pagenumber_ebook=227,pagenumber_book=214 与圆（x-m）2+y2=（a-m）2（由对称性，设0＜m＜c），消去y得，

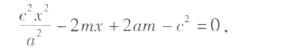
pagenumber_ebook=227,pagenumber_book=214

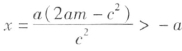求得两根x=a及，其中 pagenumber_ebook=227,pagenumber_book=214 。

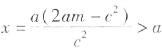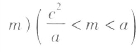若 pagenumber_ebook=227,pagenumber_book=214 ，则，因此，结合前面的结论知：球半径为（a- pagenumber_ebook=228,pagenumber_book=215 时，小球可坠杯底。

对于双曲面型的情形，相应双曲线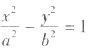 pagenumber_ebook=228,pagenumber_book=215 与圆的方程（x-m）2+y2=（m-a）2（m＞c），消去y得，，求得两根x=a和x=。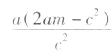

若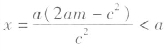 pagenumber_ebook=228,pagenumber_book=215 ，则，从而，结合已有结论得，球半径为（m-a）时，小球可坠杯底。

这是将课堂教学置于数学文化背景下进行，收到了意想不到的教学效果，激发了学生学习数学的兴趣，学生不仅学到数学知识，学会分析问题、解决问题，更重要的是体会到数学在解决实际问题的作用，把数学当作充满智慧、灵性和创造性的人类活动。

（2）课堂数学注意与其数学文化背景的联系。例如，在学习无理数之前，建议学生查阅有关无理数历史资料，主要是古希腊和中国对无理数的认识。

古希腊的毕达哥拉斯学派的希帕苏斯（Hippasus，公元前4世纪左右），首先发现了正方形与对角线之比不能用整数之比来表示。毕达哥拉斯学派所信仰的哲学信条是“万物皆数”，认为数是正整数，分数可以看作两整数之比。他们认为希帕苏斯的发现与其学派的信条相抵触，因而，把希帕苏斯抛入大海。用分数不能表示边长为1的正方形的对角线的长度，这件事使古希腊数学家感到恐慌，在数学史上有人称之为“第一次数学危机”。

而古代中国，对于无理数的认识则不同，认为无理数没有什么特别不同，只是开不尽方而已。《九章算术》第四章“少广”章开方术中称：“若开之不尽者，为不可开，当以面命之。”即如果被开方的数非完全平方数，则开方不尽而有余，称为“不可开”，此时，就“以面命之”。刘徽在注释《九章算术》中对于开方不尽的数如何求其平方根的近似值的问题，采用继续开方，求其微数的方法。他逐次以微数为分子，并分别以十、百等数为分母，即“其一退以十为母，其再退以百为母”，“退之弥下，其分弥细”，等开到某位时，虽弃其所余，但误差甚微，“不足言之也”。这是由于古代中国数学“重算法轻算理”的结果，没有对无理数有理性的认识。

（3）数学课堂教学注意与其他学科的联系。例如，比较有意思的求球体积的阿基米德的平衡法，他利用物理的标杆原理来求得。具体是这样：

设球的半径为R（如图7-3），以AB，CD为两条母线的圆柱与球外切，N，S是圆柱的两底面圆心，圆锥的母线NL，NK分别经过圆柱相应母线与球的切点，作球的大圆面以及圆柱、圆锥的轴截面。

延长SN到T，使得TN=2R。在与N距离为x处分别割出球、圆柱、圆锥的厚度为Δx的三个薄片（可看成近似的圆柱体）。它们的体积分别是

球薄片：πx（2R-x）Δx，

圆柱薄片：πR2Δx，

圆锥薄片：πx2Δx。

将球薄片与圆锥薄片悬挂在点T处，圆柱薄片仍留在原处，以N为支点考虑两边的力矩（不妨设想比重为1），

左力矩=［πx（2R-x）Δx+πx2Δx］2R=4πR2xΔx，

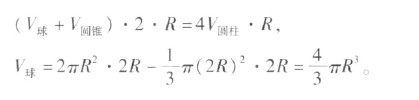
pagenumber_ebook=229,pagenumber_book=216