如开设讲座、采集数学建模问题、研究建模方案、撰写建模小论文等，有些建模问题比较复杂，可以将其分解、分步解决，或在教师带领下解决某些环节，其具体求解过程可留给学生课后解决，最后再组织学生宣讲、交流或写成小论文，这种“零存整取”的做法，既发挥了教师的主导作用，体现了以学生为主体的原则，又培养了学生的探索精神和数学能力。......
2023-08-13
数学教育价值—解析《数学教学论》
【摘要】：数学文化的内涵的揭示，决定数学文化的教育价值的转变，影响教育工作者的教育观。所谓教育价值，是指教育对社会或个人等主体的存在或发展具有的意义或价值，数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。从我国教育现实情况来看，视数学的教育价值过于工具性，体现在数学在各种考试文化中的核心和关键学科地位。
数学文化的内涵的揭示，决定数学文化的教育价值的转变，影响教育工作者的教育观。
传统上，人们认为数学是属于自然科学，是自然科学的一个门类，只关注其科学性的一面，而忽视其人文特性，这样容易造成数学与人文、社会科学之间的学科裂痕。我国数学教育多年以来，一直非常重视数学的严密性、逻辑性、抽象性的教育，关注的是数学的科学真理性，却剥离了数学生动活泼的创造性的一面，使得数学成为“冷冰冰的美丽”。表现在数学教育上以传授严格的数学定义、公式、算法为主，强调严格的练习速度和熟练程度，偏重于数学解题，解题能力强认为就是数学好。实践证明，这种传统意义上的数学教育有着局限性。
现代科学的分类已经把数学从自然科学中分离出来，数学单独成为一类，与哲学、自然科学、社会科学等大学科并列。这种分类的意义在于，数学不仅作为一门科学真理，而且与其他学科有着广泛的联系。将数学以数学文化的观念来理解，涵盖两种基本特征：抽象性和逻辑性，数学的理性精神[7]，也就是科学精神和人文精神。
数学文化的两种特征表现在数学教育上，其教育价值是什么？
所谓教育价值，是指教育对社会或个人等主体的存在或发展具有的意义或价值，数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。
（一）科学方面的教育价值
科学方面的教育价值，主要是指通过严格的数学证明和计算，解决一些数学问题，从而培养人具有严谨朴实的科学态度，使人思维严密，做事有条理；数学文化在生产、生活领域发挥工具性作用和技术性作用，能够使人们更好地认识自然、从事生产、改造自然。这是数学作为一门科学所决定的。
然而，在我国传统文化体系中，科学是没有地位，受到歧视，最多也只是统治阶级为了统治的需要用数学来管理国家、社会事物，如我国纪元前后的数学经典著作《九章算术》明显带有这种特性。从我国教育现实情况来看，视数学的教育价值过于工具性，体现在数学在各种考试文化中的核心和关键学科地位。因此，在数学文化教育中，需要进一步加强数学的科学性教育，提高学生的数学素质，让学生在中学阶段掌握数学的基础知识、基本技能、基本思想，用数学进行思考，提高用数学解决实际问题的能力。
在《周髀算经》中就有记录关于“矩”的用法。刘徽测量海岛的高度，他创造性地使用二次测量的办法来测量海岛的高度，这种测量不受自然环境和地理位置等因素的影响，借助于一根标杆即可测量海岛的高度。
《海岛算经》第一题，“今有望海岛，立两表齐高三丈，前后相去千步，令后表与前表参相直。从前表却行一百二十三步，人目著地取望海岛峰，与表末参合。从后表却行一百二十七步，人目著地取望海岛峰，亦与表末参合。问岛高及去表各几何？”
答曰：“岛高四里五十五步，去表一百二里一百五十步。”
术曰：“以表高乘表间为实。相多为法，除之，所得加表高，即得岛高。求前表去岛远近者，以前表却行乘表间为实，相多为法，除之，得岛去表里数。”
用现代数学符号可表示为：
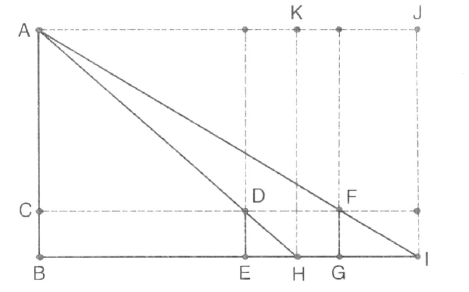
图7-1
这是两次用表对同一事物在不同地点进行测量，利用这两次测量数据的差进行计算。可用出入相补原理证明。
由图7-1可知，矩形FJ=矩形FB，矩形DK=矩形DB，
两式相减得，矩形FJ-矩形DK=矩形EF，
即AC×（GI-EH）=DE×EG，由此可得上述两个公式。
这说明人类在历史上总结并创造的方法具有科学性，可以运用其科学性来解决具体的实际问题，让学生在数学文化背景中掌握某种方法、技能解决实际问题，体现数学文化的科学价值。
（二）人文方面的教育价值
人文方面的教育价值，主要是指数学能够使人更具有理性，数学可以提高人的审美能力，强调数学过程的数学化以及数学具有理性的体验、情感、意志、价值观，数学具有德育功能，使人求真、求善、求美。
欧洲文艺复兴以来，唯科学主义开始盛行，对人文知识方面却受忽视。到了20世纪，人们开始意识到科学主义的缺陷，回归到对人文主义的重视，将科学主义和人文主义融合起来。我国数学教育受到这种思想的影响，开始审视并检讨数学教育现实，认识到我国数学教育传统优点之外，也认识到其存在的问题，拼弃对学生实施高强度、高难度的数学教学活动，遏制单纯的数学工具主义和冰冷的技术主义等等，而凸显数学的人文精神，培养学生对数学的好奇心和求知欲。
如关于黄金分割数，从学生熟习的门框、像框的宽与长之比开始谈起，然后，推广到世界各地的建筑，优秀的艺术作品等。如埃及的金字塔的高与底座的边长之比为黄金分割数；希腊神庙，神庙的高与宽之比为黄金分割数；人的身体里有黄金分割数，肚脐到脚底的距离与头顶到脚底的距离之比为黄金分割数；五角星（如图7-2）
。1970年以来，我国著名的数学家华罗庚教授推广使用优选法，就是应用黄金分割，即利用反复在线段上取黄金分割点的方法做实验，较快地找到了最佳方案，减少试验次数。
图7-2
学生可以通过与黄金分割数有关的知识背景的应用，激发学生学习数学的兴趣，同时扩展学生的数学知识，从而逐步形成正确的数学观。
有关数学教学论的文章
- 详细阅读
-
中国数学教学简介-数学教学论详细阅读
1903年，清朝公布“癸卯学制”，基本上仿照日本学制，各级学校都规定有数学课程。从1919年五四运动到1949年10月1日中华人民共和国成立，这个时期是中国社会发生伟大变革的历史时期，在这个时期，中国数学教育进一步与国际数学教育相交流，中国数学教育也成为世界数学教育的一部分。中小学的课程已恢复正常，并在东北地区的中小学数学课程中引入苏联教材的内容，逐步改进课程的内容，实行统一编制的教材，新民主主义教育开始进入新阶段。......
2023-08-13
-
《数学教学论》：数学语言及其教学详细阅读
数学发展史表明，数学的发展与数学语言的创造是分不开的。我国数学教育学者郑毓信指出，应当将熟练掌握数学语言作为数学教育的一个基本目标，包括帮助学生学会数学地表达，数学地理解等，也就是说，我们不应将“数学地说”与“数学地写”等仅仅看成帮助学生掌握相应的数学知识与技能的一种手段，而应将其本身看成数学教育的重要目标之一因此，探究数学语言的特点及其教学是很有意义的。......
2023-08-13
-
数学情感、态度价值观的科学涵义—《数学教学论详细阅读
“情感、态度与价值观”教育目标源于人本主义课程教育目的。基于以上教育思想以及教育心理学理论知识，我们不难勾画出数学“情感、态度与价值观”的科学涵义。教育心理学指出，情感是人对客观事物的态度的体验，也即对客观事物是否满足主观需要的评价的反映；态度是指对某一客观事物所持的评价和行为倾向；价值观是态度的凝练，体现个体对事物本质的认识和理解，融进了人格而形成的。......
2023-08-13
-
数学教学论：评估课程发展详细阅读
在上一小节中对课程教学评价作了概述，本小节里要介绍数学课程教学的发展性评价。数学课程的发展性评价来源于形成性评价，但更加强调以人的发展为本的思想。第六，数学课程教学的发展性评价应该强调定性评价与定量评价的综合运用。理论界较为一致地认为，教学的发展性评价对于促进教学具有重要的作用。......
2023-08-13
-
数学教学论：深化数学文化内涵详细阅读
近年来，作为教育形态的数学，对数学的形式化的追捧，认为数学只有用式子来表示才被认为是数学。所以，我国数学教育专家已经认识到这一点，提出数学教育应“注重实质，深化形式”，从另一个层面来看，也就是数学教育应加强数学文化的教育。这种观点将数学以更宽泛的意义上来理解一数学文化，那么，数学文化的内涵是什么？当前，我国对数学文化的内涵理解大体可以从三个角度来理解，即人类文化学、数学活动、数学发展史。......
2023-08-13
-
数学教学论：优秀的教学途径详细阅读
作为教育形态的数学文化，必然要求如何进行数学文化的教学。数学文化的教学可以在课堂内外进行，其基本的前提条件是必须在教师的指导下进行。数学文化课外活动的形式是多种多样的。有的以学生写数学小论文的形式来进行，以充分发挥学生数学方面的聪明才智，增强学生的创新意识，提高学生发现问题和解决问题的能力。......
2023-08-13
-
古罗马数学课程概述-数学教学论详细阅读
古罗马原是意大利半岛上的一个奴隶制小城邦。可见，古罗马学校无论大、中、小学都教授数学。罗马学校只教那些必要的十分实用的数学知识，如简单的测量和计算等，古希腊人高深的理论数学知识完全没有包括在内。罗马人在数学上一无创造，从希腊人达到的高峰上跌落下来。不仅如此，古希腊的数学成就也没能通过罗马传入近代欧洲，造成这种情况的主要原因是罗马不重视数学教育和理论数学。......
2023-08-13
相关推荐