数学教学论：新课程内容标准的设计

2023-08-13 理论教育版权反馈

【摘要】：（一）义务教育阶段数学新课程的内容标准设计1.内容标准的结构义务教育阶段数学新课程的内容标准部分针对三个学段分别展开。与此同时，数学新课程还增加了统计与概率、空间与图形等密切联系学生现实生活、反映社会发展需要的新内容，并设立了“实践与综合运用”，以促使学生体会各部分内容之间的联系，发展其综合解决问题的能力。

（一）义务教育阶段数学新课程的内容标准设计

1.内容标准的结构

义务教育阶段数学新课程的内容标准部分针对三个学段分别展开。为了体现义务教育阶段数学课程的整体性，新课标通盘考虑了9年的课程内容；同时，根据儿童发展的生理和心理特征，将9年的学习时间具体划分为三个学段：第一学段从一年级到三年级，第二学段从四年级到六年级，第三学段从七年级到九年级。在各个学段，新课标安排了“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用”4个学习领域。课程内容的学习，强调学生的数学活动，发展学生的数感、符号感、空间观念、统计观念，以及应用意识与推理能力。

表2-1　内容结构

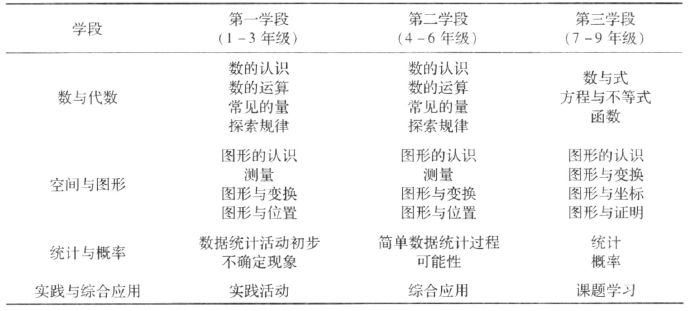
pagenumber_ebook=61,pagenumber_book=48

针对每个学段中的4个学习领域，义务教育阶段数学新课标分别阐述各学习领域的一般目标，然后分别阐述每个学习领域中各部分内容的具体目标，最后结合具体目标给出一定的案例。

2.内容标准的特点

一方面，义务教育阶段数学新课标继承我国数学教育的传统，重视学生对必要的基础知识和基本技能的熟练掌握；另一方面，它又考虑到时代的发展、数学的发展，倡导义务教育的数学课程应该实现人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展。

（1）“人人学有价值的数学”。倡导新数学课程要向学生提供现实的、有趣的和富有挑战性的数学学习内容，这些内容将成为学生主动地从事观察、实验、猜测、验证、推理与交流的主要素材。例如，第一学段（1-3年级）“数与代数”内容领域，关于“常见的量”的具体目标包括：在现实情境中，认识元、角、分，并了解它们之间的关系；能认识钟表，了解24时记时法；结合自己的活动经验，体验时间的长短。这些具体目标强调，在教学中要引导学生联系自己身边具体、有趣的事物，通过观察、操作、解决问题等丰富的活动，感受数与量的意义。

义务教育阶段数学新课程的内容标准进一步强调，数学内容以“问题情境——建立模型——解释、应用与拓展”的基本模式展开，这种模式更适合学生在有限的学习时间里接触、了解和掌握数学。“有价值的数学”与学生的现实生活及以往的知识体验有密切的关系。例如，第二学段（4-6年级）的“数与代数”内容领域，关于“数的认识”的具体目标包括，进一步体会数在日常生活中的作用，会运用数表示事物，并能进行交流等；关于“正比例、反比例”的具体目标，要求学生在实际情境中理解什么是按比例分配，并能解决简单问题，通过具体问题认识成正比例、反比例的量，等等。

（2）“人人都能获得必需的数学”可以理解为，数学课程应该对学习内容进行精选，满足学生适应未来社会生活和进一步学习的需要。义务教育阶段数学新课程较大幅度地降低了繁杂的数字运算要求，如删除带分数的四则运算，降低代数式运算、几何证明的要求，淡化了某些非数学本质的术语和概念（如乘数与被乘数）。与此同时，数学新课程还增加了统计与概率、空间与图形等密切联系学生现实生活、反映社会发展需要的新内容，并设立了“实践与综合运用”，以促使学生体会各部分内容之间的联系，发展其综合解决问题的能力。另外，要使学生认识到数学的价值，了解数学在文化中的地位和在社会生活中的作用。例如，在第三学段（7-9年级）的“课题学习”内容领域中明确指出：在本学段中，学生将探讨一些具有挑战性的研究课题，发展应用知识解决问题的意识和能力；同时，进一步加深对相关数学知识的理解，认识数学知识之间的联系。

（3）“不同的人在数学上得到不同的发展”是指数学课程要面向全体学生，让不同的学生在数学学习上都能成功。新的数学课程具有较大的弹性，要求最大限度地满足每个学生的数学需要，最大限度地发展每个学生的智慧潜能，而且能为有特殊才能和爱好的学生提供更多的发展机会。要关注在学习上暂时有困难的学生，不让一个学生掉队。

义务教育阶段数学新课程对教学目标的描述更多地从学生发展角度展开，在对基本知识、基本技能做明确的目标规定后，更多的描述是使用“探索，体验，体会”等词汇，便于我们在教学中针对不同的学生群体选择不同程度的内容。

（二）普通高中阶段数学新课程的内容标准设计

1.内容标准的结构

这部分针对必修课程和选修课程的各个模块或者专题，说明应该关注的学习内容、建议的课时数以及相关的内容案例。其中构成必修课程的5个模块的内容为：

数学1：集合、函数概念与基本初等函数I（指数函数、对数函数、幂函数）；

数学2：立体几何初步、平面解析几何初步；

数学3：算法初步、统计、概率；

数学4：基本初等函数Ⅱ（三角函数）、平面上的向量、三角恒等变换；

数学5：解三角形、数列、不等式。

上述内容覆盖了高中阶段传统的数学基础知识和基本技能的主要部分，但是在保证打好基础的同时，要强调这些知识的发生、发展过程和实际应用，而不在技巧与难度上做过高的要求。

构成选修课程的4个系列的内容分别为：

系列1（由2个模块组成）：

选修1-1：常用逻辑用语、圆锥曲线与方程、导数及其应用，

选修1-2：统计案例、推理与证明、数系的扩充与复数的引入、框图。

系列2（由3个模块组成）：

选修2-1：常用逻辑用语、圆锥曲线与方程、空间中的向量与立体几何，

选修2-2：导数及其应用、推理与证明、数系的扩充与复数的引入，

选修2-3：计数原理、统计案例、概率。

系列3（由6个专题组成）：

选修3-1：数学史选讲，

选修3-2：信息安全与密码，

选修3-3：球面上的几何，

选修3-4：对称与群，

选修3-5：欧拉公式与闭曲面分类，

选修3-6：三等分角与数域扩充。

系列4（由10个专题组成）：

选修4-1：几何证明选讲，

选修4-2：矩阵与变换，

选修4-3：数列与差分，

选修4-4：坐标系与参数方程，

选修4-5：不等式选讲，

选修4-6：初等数论初步，

选修4-7：优选法与试验设计初步，

选修4-8：统筹法与图论初步，

选修4-9：风险与决策，

选修4-10：开关电路与布尔代数。

2.内容标准的特点

我国新一轮普通高中数学课程改革有其自身的新理念，它在内容标准方面的反映，主要体现出以下三个方面的特点：

（1）课程内容的基础性。上述必修课程的5个模块的内容是每一个高中学生都要学习的。其中算法是新增加的，而向量、统计和概率是近些年来不断加强的内容，其它内容基本上都是以往高中数学课程的传统基础内容，当然有些内容在目标、重点、处理方式上发生了变化。这些内容对于所有的高中学生来说，无论是毕业后直接进入社会，还是进一步学习有关的职业技术，或是继续升大学深造，都是非常必要的基础。

选修课程分为4个系列，是为了给将来发展方向不同的学生提供更宽泛、更进一步的基础。其中，选修系列1是为准备在人文、社会科学方面发展的学生设置的，选修系列2是为准备在理工、经济方面发展的学生设置的，选修系列3和系列4则是为所有学生进一步拓宽或提高数学素养而设置的。这些内容仍然是为学生的进一步发展奠定基础，这样安排更加方便学生按照自己的意愿，来规划个人的进一步发展，为不同发展方向的学生提供不同的基础。

（2）课程设计的选择性。必修课程和选修课程的各个系列全都划分成模块或专题，是为了方便学生选择课程内容、制定学习计划。其中，必修课程、选修系列1和系列2的每一个模块，都安排了36课时（约半个学期）的学习内容，选修系列3和系列4的每一个专题，都安排了18课时的学习内容。每个学生在学期开始时，可以根据自己的学习基础和发展方向，选择不同模块的内容，制定各自不同的学习计划，还可以在学习一个阶段之后，根据自己的学习情况，调整、变更学习计划。这样就为不同学生的发展打好不同的基础，提供了充分的选择性。

（3）学习方式的多样性。在内容标准这部分还涉及这次高中数学课改的亮点，即学习方式的多样性。高中数学课程设置了数学探究、数学建模、数学文化内容，这些内容以不同的形式渗透在各个模块和专题内容中，它们将为学生提供更广阔的发展空间，也为改变学生的学习方式提供了素材。普通高中数学新课标要求每个学期都至少有一次完整的数学探究、一次数学建模活动，而数学文化内容要与各模块的内容有机结合。这些内容的增加，使得数学课程的内容更加丰富，更具有立体感。

数学教学论：新课程内容标准的设计

相关推荐