古印度数学课程简介及影响

2023-08-13 理论教育版权反馈

【摘要】：印度也是世界上文明发达的古国，但是由于缺少可靠的记录，对古代印度数学的发展却知道很少，因而对古印度的数学课程的介绍也就相应有点简单。印度的数学发展是在埃及、巴比伦、希腊、中国之后，但也可追溯到公元前2000多年。印度的数学和占星术有关，而占星术又和宗教与农业有密切联系。古代印度设有宫廷学校和祭司学校。附设在神庙内的一种学校，称为神庙学校。

印度也是世界上文明发达的古国，但是由于缺少可靠的记录，对古代印度数学的发展却知道很少，因而对古印度的数学课程的介绍也就相应有点简单。

印度的数学发展是在埃及、巴比伦、希腊、中国之后，但也可追溯到公元前2000多年。印度在历史上屡次遭受到外族的侵略，公元前500年左右波斯王大流士征服了印度的一部分土地。公元前326年马其顿王亚历山大侵入旁遮普，后来建立了莫尔雅帝国（Maurya Empire），并立即扩展到印度全部以及中亚细亚的一些地区。最著名的莫尔雅统治者是乌索库（King Asoka，公元前272-232年）。在乌索库之后，印度遭到一系列的侵略，直到笈多王朝（Gupta dynasty）（大约公元400年），才处于本印度皇帝的统治下。笈多时代是梵文复兴的黄金时代，印度成了学术、艺术和医学研究、发展的中心。大约在公元450年到14世纪末，印度又受到许多次外来的侵略。匈奴人先来；然后在8世纪，阿拉伯人又来了；到了11世纪，又有波斯人的入侵。因而早期的印度数学就受到巴比伦、埃及和希腊的影响，后来又受到中国的影响，当然他们也有很多独特的创造。

印度的数学和占星术有关，而占星术又和宗教与农业有密切联系。他们的数学书籍带有浓厚的宗教气味，将计算方法和结果用语句难懂的诗歌写出来，以至后人不易理解。

古印度数学史大概可分为两个时期：礼经时期（The Sulvasutra Period）和历算时期（The Astronomical and Mathematical Period）^[3]。

（一）礼经时期

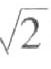《礼经》一书为公元200年以前宗教经典，所含算学有勾股定理、方圆面积等，都应用于宗教祭礼，故称公元200以前算学为礼经算学。这个时期的数学未能流传于后，但近世的研究，使人们对其有了一些了解，如用单位分数表示某些似值：是 pagenumber_ebook=22,pagenumber_book=9 相当好的近似值。又给出π=，其数值等于3.088。

但在耆那教（公元前6世纪在印度兴起的一种宗教）的经典中，却可以找到较好的π=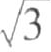 pagenumber_ebook=22,pagenumber_book=9 =3.162。

此外还知道圆的面积等于一个矩形的面积，这个矩形的长等于半个圆周，高等于圆的半径。

（二）历算时期

始于公元400年，终于1200年，这是印度数学的全盛时期。初期研究为测量天体推算历法等，至9世纪，始有纯粹算学著述。这一时期的著名数学家有：阿里亚布哈搭（Aryabhata，即圣使，约在公元467年左右）、瓦拉哈米希拉（Varahamihira，即彘日，约公元587年左右）、婆罗门芨多（Brahmagupta，即梵藏，约公元598年左右）、玛哈维拉（Mahavira，即大雄，约公元850年左右）、婆什迦罗（Bhaskara，1114-1178）等。印度数学家的著作主要是天文学、算术、代数等方面的，有时也涉及度量术和三角学。

公元6世纪，关于印度历法的重要著述有5种之多，而彘日集其大成。其所撰书中，采十九年七闰制，所采用的正弦算法，也来源于希腊数学。

圣使和后世的数学家的书中研究过面积、体积算法、圆周和直径的关系。他们此处取用古率π=3，而彼处又录及等率。圣使曾求得π=3.1416，并讨论了一次不定方程的解法。圣使的研究工作还涉及到一些三角学方面的领域。

梵藏研究的学术领域，也源于希腊数学。他将已知三角形三边求面积的方法进行推广，应用于圆内容四边形。他还能解一次及二次不定方程，其解一次不定方程的解法，用辗转相除如同求最大公因数法，似与《孙子算经》“物不知数”题解法及历算家求上元积年算法相同。他独立运用了负数，还曾研究过二次方程、圆周率。

大雄研究了大数表示法和不定方程。大雄书中的一次不定式问题，和《张邱建算经》中的题目几乎一样。

婆什迦罗以所著《丽罗娃提》一书而出名，这是东方算术和计算方面的重要著作，他承认方程的负根，提出了平方根的双值性，并解出了某些特殊的高次方程。

值得一提的是，1、2、3、4、5、6、7、8、9被人们称为“阿拉伯数码”，这实在是历史的误会。实际上印度早在公元前4世纪已开始使用类似上述的数码，比阿拉伯使用类似数码要早得多，因而应该称为“印度数码”才更合适些。

印度数学发展如上所述，直到18世纪中叶沦为英国殖民地之前，数学发展水平并无大的提高。印度是一个具有浓厚封建和宗教色彩的封闭王国，生产是典型的小农生产方式，经济相当落后，佛教、印度教盛行，国家没有办教育的传统，它是个人的事业，属于宗教事业的一部分^[4]。因此，这一时期印度教育是一种传统的、封闭的宗教教育和人文教育，与社会生产和科学技术的发展相去甚远。反映在中学课程上，就形成了重视人文学科、宗教教义和民族语言的课程观。小学课程则注重读、写、算以及宗教经书的学习，教学方法基本上是注入式、填鸭式，这种本土教育模式以及与之相应的课程观，一直延续到殖民时期的初始阶段仍占主导地位。

古代印度设有宫廷学校和祭司学校。前者设在国王所在地的宫廷内，专供王子或高级官吏（大臣）子弟就学，以培养奴隶主国家的高级文武官吏为主要任务。后者设在大寺庙（院）里，专供高级僧侣子弟就学，其主要任务是训练未来的高级僧侣，所以又称僧侣学校。印度的宫廷学校和寺院学校，都把学习婆罗门教的经典——《吠陀》放在首位。年老的大臣、僧侣和官吏们，认为这些经典最适宜教诲青年，便于他们将来为官为僧。当然，有些宫廷学校和祭司学校开设的课程也有天文、数学、建筑、医学、地理等，因为对未来的奴隶主国家的高级官吏和高级僧侣来说，无论是管理国家，主持寺庙或兴建宫殿、陵墓，懂得一些数学的基本知识是非常必要的。

为了适应人们对宗教或神的信仰，建筑了各种庙寺和寺院。附设在神庙内的一种学校，称为神庙学校。就学校的地位而言，神庙学校比宫廷学校和祭司学校的地位要低，神庙学校的培养目标较为广泛，它既培养一般官吏、一般僧侣人员，也培养为皇家修建宫殿、陵墓、寺庙及医治疾病的人员，因此，数学成了各类神庙学校的必修课程。印度的神庙学校，都要收取高昂的学费，仅从这一点就可以知道，神庙学校绝非一般人家的子弟所能上得起的。神庙学校的教学方法非常简单，一般只限于教师问学生答，文字书写和背诵占很重要地位。在整个教育、教学过程中，都特别注意和加强宗教神学精神和巫术思想的灌输。

“古儒”学校也是在古印度出现的一种学校。“古儒”学校出现的时间较晚（公元前8世纪），它是由在印度被称为“古儒”阶层的人物设置起来的学校，“古儒”是指那些对婆罗门教的教义（吠陀经）有较深研究而愿专门致力于青年教育工作的人。“古儒”学校设在“古儒”家庭中，入学年龄一般在七八岁以上，学习年限不定。学习的课程有计算方面的内容，“古儒”对有些学生还开设天文、几何等课程，但“古儒”学校的全部学科都渗透着婆罗门教的神学精神。

物换星移，后来伊斯兰教进入印度。于是印度教和伊斯兰教这两种宗教派别以其不同的文化和信仰深深地影响着印度教育的发展，形成了两种不同形式、内容、目标的教育形式，即印度教教育和伊斯兰教教育。印度教小学的培养目标及其特征决定其课程设置，印度教小学课程设置主要包括书写、朗读，算术的初级练习、以及写商业信件和诉状、读梵文叙事诗、学初等数学等高级课程，在教学中先教写后教读，再教一些高级课程。

印度穆斯林教育的教育目的是使学生为现世和来世作准备，伊斯兰教小学课程包括读、写、算以及《古兰经》中的部分内容，在教学过程中，先教读后教写，这一点与印度教小学不同。

印度教中学与伊斯兰教中学的课程设置有较大区别，主要表现在两个方面：第一，表现在宗教神学上，这是最主要的区别；第二，表现在学科的广泛性以及对古希腊文化的吸取上，穆斯林课程比印度教课程广泛得多。但二者也有共同点，它们都注重古典学科教育，反映出一种古典人文主义课程观，他们开设的课程中相同的就有逻辑、文学和天文学^[5]。在印度，数学的发展始终与天文学联系在一起，数学著作大都是天文学著作中的某些篇章^[6]。

古印度数学课程简介及影响

相关推荐