古巴比伦数学课程简介—《数学教学论》

2025-09-29 理论教育版权反馈

【摘要】：我们把这一地区在漫长的历史中形成的数学教育称为古巴比伦的数学教育，其数学课程也作相应约定。巴比伦数学比较发达。一些应用问题的解决，表明巴比伦人已经有解一次、二次数字方程的经验公式，他们还讨论了某些三次方程和双二次（四次）方程。“星期”的来历也是巴比伦人的贡献。研究表明，古巴比伦天文学很发达，已发现了黄道角，能测出日食、月食。由上可知，古巴比伦的数学水平相当高，而且内容丰富多彩。

亚洲西部的底格里斯河与幼发拉底河之间的地带，通常叫做两河流域，这块地方古代叫做美索波达米亚，和尼罗河流域一样，也是人类文明的摇篮。在公元前2025年就有了人类的文明活动；在公元前2025年左右，有苏美尔人建立起奴隶制国家，其后有亚述帝国崛起1000多年；公元前18世纪，古巴比伦王国建立起来；新巴比伦王国则建立于公元前626年。我们把这一地区在漫长的历史中形成的数学教育称为古巴比伦的数学教育，其数学课程也作相应约定。

巴比伦数学比较发达。巴比伦人在公元前2025年起到希腊数学兴起为止的楔形文字表明，他们的贡献可与古埃及相媲美。所谓楔形文字是公元前4000-前2025年，两河流域的苏美尔人创造的，文字最初是刻在石头上的，以后改用泥板。先用削尖的木笔在软泥板上刻写，然后烧或晒干，使它坚硬如石。字的形状象楔子，所以叫楔形文字。这种文字被埋在地底下数千年之久，直到100年前才为现代人所知。现已发现的楔形文字泥板中就约有300块是纯数学内容，现代学者就通过大量的泥板去探索当年两河流域的数学发展情况。

（1）约在公元前1800-公元前2025年，巴比伦人已采用较系统的六十进位值制记数法。如：

其中 pagenumber_ebook=19,pagenumber_book=6 表示10，表示1，并出现了60进位的分数，用与整数同样的法则进行运算。大约在公元前2025年的第7289号耶鲁（数表）书板上发现了对于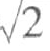的一个非常值得注意的近似值：

达到了相当高的精确程度。

（2）约200块泥板是各种数表。有平方表、立方表、乘法表、倒数表，甚至还有指数表。指数表可能是用来计算复利的，倒数表是将除法化为乘法进行计算时使用的。

（3）大约在公元前2025年，巴比伦人已经由算术向代数过渡。一些应用问题的解决，表明巴比伦人已经有解一次、二次数字方程的经验公式，他们还讨论了某些三次方程和双二次（四次）方程。

研究者发现汉穆拉比时代（公元前18世纪）的泥板上有二次方程的问题，并看出了从算术到代数的飞跃。例如：“两个正方形面积之和是1000，其中一个的边长是另一个边长的 pagenumber_ebook=20,pagenumber_book=7 少10，问各长多少”？这相当于解联立方程

答案是x=30，y=10。

（4）在几何方面，他们已经掌握了“直角三角形的两直角边平方和等于斜边的平方”——勾股定理，给出了一些勾股数，他们还知道了相似三角形对应边成比例，会计算简单的直边形面积和简单立体的体积。在圆面积计算中用公式S=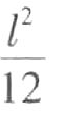 pagenumber_ebook=20,pagenumber_book=7 （l表示圆周长，π=3），他们不是专为几何而研究几何，总是在解决实际问题时才去研究几何，由此发展了实用几何。(https://www.chuimin.cn)

（5）商业发展所产生的高利贷，引出了复利问题的计算。巴比伦位于亚、欧、非大陆之间，地理位置重要，交通发达，为重要的贸易地区，因而巴比伦商业发达，数学为商业服务是其突出特点，由此形成了商业实用数学。复利是商业数学必然要遇到的问题，楔形文字的记载中涉及到复利的问题就有：“设利率是20%，何时能使本利和是本金的2倍？”这将导致解指数方程（1.2）x=2。在泥板中还发现了许多帐簿、账单、收据等商用的文献。

（6）天文学的发展促成了关于角的度量和三角学的萌芽。天文学中由经验得到的某些相依关系的详明表，我们可以看到函数关系的原型。

巴比伦人很早就已使用日历。他们的年是从春分开始的，并且一月是以金牛座命名的，这是因为在公元前2025年左右春分时太阳在金牛座。因此可以说巴比伦人远在公元前四五千年就有了某种历法推算，似乎不无道理。

“星期”的来历也是巴比伦人的贡献。约在公元前2025年，由于巴比伦天文学的发展，促进了大数的运算。其中一个内容是把每周分为7天，与包括日、月在内的7个行星相当。每一星神主管一天：太阳神主管星期日，其余6天分别由月神、火星神、水星神、木星神、金星神和土星神主管。“星期”就是星的日期，这也流传至今，为全世界所通用。

在一切古代民族中，天文学总是发达较早的一门学科。这一方面是由于农业生产的需要，另一方面古人大多迷信天象和人事的凶吉有关，从而有占星之术。占星者时时注意日月星辰的运行，有可能逐渐发现其中的规律，于是便产生了天文学。研究表明，古巴比伦天文学很发达，已发现了黄道角，能测出日食、月食。

（7）后期的楔形文献中，已出现了零的萌芽。零的发现虽然是位值制的必然产物，可是须在计算技术相当完备之后才有可能出现。研究表明，公元前6世纪以后的泥板有时用空出一格来表示“零”；约在公元前200年，才有零号的记载，但还未用在计算之中。

由上可知，古巴比伦的数学水平相当高，而且内容丰富多彩。

亚述和巴比伦都是奴隶制国家，为了培养自己的接班人，奴隶主阶级便发展教育事业。巴比伦的教育具有鲜明的阶级性，僧侣和文士是统治阶级在文化教育领域里的代理人，巴比伦的国王自命为高级僧侣。当时的寺庙不仅负有宗教活动的职责，还管理观测天象，指导灌溉、发展农业，指导商业及建筑工程等，实际上是兼理僧俗双重任务的机构。僧侣是文化层次最高的居民，他们为培养接班人而重视教育，可能当时产生过寺庙学校。同时，政府部门的管理工作需要大量能写会算的文士做官吏，商业也大量需要这种人士。为了培养文士，政府开始举办学校，文士也可办私立学校，于是产生了学校教育。

学习的课程是书写和计算，发现的泥板书就是当时的教科书，这些课程难度较高，作业量大。在教学方法上，老师一般强调机械式地练习，死记硬背，并且采用体罚。

古巴比伦数学课程简介—《数学教学论》

相关推荐