,P2006的位置,求点P2006的横坐标.如图②,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3…......
2025-09-29
高斯被形容为“能从九霄云外的高度按照某种观点掌握星空和深奥数学的天才”,创造力与直觉、卓越的计算能力、严密的逻辑推理和谐地组合在一起.高斯所著的《算术探索》一书,被誉为“数学的宪章”,开创了现代数论研究的新纪元.
知能概述
解决实际问题以及计算机的运算中,常常需要对一些数据进行取整运算(也称“高斯函数”),即去掉一些不是整数的实数的正的纯小数部分,而用不超过它的最大整数取而代之.
对于任意实数a,通常[a]表示不超过a的最大整数,如[3.6]=3,[-3.6]=-4,[5]=5等.{a}=a-[a]称为实数a的小数部分.[a]有以下基本性质(当且仅当a为整数时,等号成立):
1.a=[a]+{a},0≤{a}<1.
2.[a]≤a<[a]+1.
3.a-1<[a]≤a.
4.[n+a]=n+[a](其中n为整数).
问题解决
例1 若![]() =s,则[s]=_________.
=s,则[s]=_________.
(“五羊杯”竞赛题)
解题思路 ![]() ,要求[s],只需估算
,要求[s],只需估算![]() 的取值范围.
的取值范围.
国际著名学术团体——罗马俱乐部在《回答未来的挑战:推进新的学习观——创新性学习》报告中指出:所谓创新性学习,就是通过学习提高一个人发现、吸收新信息和提出问题的能力,以迎接日新月异的变化.
[x]的人文意境
如图,在直角坐标系中作出函数y=[x]的图象,形象再现诗的意境:
欲穷千里目,
更上一层楼.
例2 设[x]表示不大于x的最大整数,则![]() 等于( ).
等于( ).
A.1001 B.2003 C.2004 D.1002
(“希望杯”邀请赛试题)
解题思路 通过放缩,估计![]() 的值.
的值.
例3 解下列方程:
(1)[1.9x]=10 (x为自然数);
(2)[3x+1]=2x-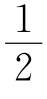 ;
;
(全国初中数学联赛题)
(3)[2x]+[3x]=8x-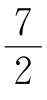 .
.
(上海市竞赛题)
分析 解与[a]相关的方程,关键是去掉符号“[]”.需灵活运用[a]的性质,并善于把估算、等式与不等式知识综合起来.如对于(3),2x-1<[2x]≤2x,3x-1<[3x]≤3x,从而5x-2<[2x]+[3x]≤5x,即5x-2<8x-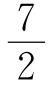 ≤5x,这样可求出x的取值范围.
≤5x,这样可求出x的取值范围.
解(3)由5x-2<8x-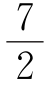 ≤5x,得
≤5x,得![]() .得8x-
.得8x-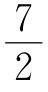 =1,2,3,4,5,∴x=
=1,2,3,4,5,∴x=![]() .经检验x=
.经检验x=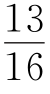 或
或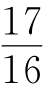 .
.
例4 (1)设x,y满足方程组![]() 求[x+y]的值.
求[x+y]的值.
(山东省竞赛题)
(2)已知x,y,z满足
求x,y,z的值.
(“华罗庚金杯”少年数学邀请赛试题)
解题思路 对于(1),3[x-2]=3([x]-2)=3[x]-6,先解关于[x],y的方程组;对于(2),由a=[a]+{a},可先求出x+y+z的值,进而分别求出[x],{x},[y],{y},[z],{z}的值.
解与取整运算相关的方程、方程组,常用相关性质,去掉“[]”符号,将问题转化为解不等式,整数既是隐含条件,又是制约因素.
例5 证明:对于任意实数x,有[x]+[x+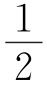 ]=[2x].
]=[2x].
证明 设x=[x]+{x}({x}表示x的小数部分).
由x-1<[x]≤x,得0≤{x}<1.
高斯函数
公元321年3月7日,古罗马皇帝君士坦丁正式宣布采用“星期制”,并规定当天为星期一.
公元2025年,德国数学家高斯在研究圆内整点问题时,引进了一个函数y=[x],[x]是表示不超过数x的整数部分.
有了高斯函数,历法学家为我们找到计算某日是星期几的公式.
例6 下面的公式可以计算某日是星期几:
![]() ,其中,x是年份,y是该年从元旦起到这一天为止的天数,[x]表示不超过x的最大整数.
,其中,x是年份,y是该年从元旦起到这一天为止的天数,[x]表示不超过x的最大整数.
若S÷7得到的余数是几,则该天就是星期几.如:余数是0表示星期日,余数是1表示星期一……
问:2025年11月25日是星期几?
(世界数学团体锦标赛试题)
分析与解 在阅读理解的基础上,代入公式计算.
∴2025年11月25日是星期五.
例5的一般形式是埃尔米特恒等式:
对任意实数x及正整数n(n>1)有:
德国发行的纪念高斯的货币.高斯给出的正十七边形可以用尺规作图的证明,这一问题的证明不仅震撼了数学界,也震撼了高斯自己的心灵.
F.克莱因曾评价高斯说:“如果我们把18世纪的数学家想象为一系列的高山峻岭,那么最后一个使人肃然起敬的巅峰便是高斯.”
1.高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.例如:[2.3]=2,[-1.5]=-2.则下列结论:①[-2.1]+[1]=2;②[x]+[-x]=0;③若[x+1]=3,则x的取值范围是2≤x<3;④当-1≤x<1时,[x+1]+[-x+1]的值为0,1,2.其中,正确的结论的序号是_________.
(四川省乐山市中考题)
2.方程6x-3[x]+7=0的解是________.
(“希望杯”邀请赛试题)
3.方程[2x]+[3x]=9x-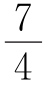 的所有解是_________.(https://www.chuimin.cn)
的所有解是_________.(https://www.chuimin.cn)
(湖北省武汉市竞赛题)
4.如果f(x)=![]() ,那么[f(2)]+[f(3)]+…+[f(100)]的值等于________.
,那么[f(2)]+[f(3)]+…+[f(100)]的值等于________.
(“五羊杯”竞赛题)
5.已知正整数n小于2006,且![]() ,则这样的n有_________个.
,则这样的n有_________个.
(全国初中数学竞赛题)
6.以下四个结论,正确的是( ).
A.[a]+[-a]=0 B.[a]+[-a]=0或1
C.[a]+[-a]≠0 D.[a]+[-a]=0或-1
(“希望杯”邀请赛试题)
7.设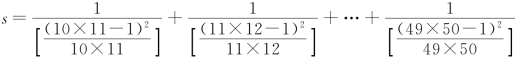 ,则[30s]=( ).
,则[30s]=( ).
A.1 B.2 C.3 D.0
(“五羊杯”竞赛题)
8.设x,y满足方程组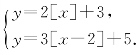 若x不是整数,则x+y=( ).
若x不是整数,则x+y=( ).
A.一个整数 B.在4与5之间
C.在-4与4之间 D.在15与16之间
(美国数学邀请赛试题)
9.正整数n小于100,并且满足等式![]() =n,这样的正整数n有( )个.
=n,这样的正整数n有( )个.
A.2 B.3 C.12 D.16
(全国初中数学联赛题)
10.设[x]表示不超过实数x的最大整数,{x}=x-[x],则![]() +
+![]() =( ).
=( ).
A.249075 B.250958 C.174696 D.251000
(“五羊杯”竞赛题)
11.解关于x的方程[x+2]+[5x+1]=9x-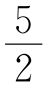 ,其中[x]表示不超过x的最大整数.
,其中[x]表示不超过x的最大整数.
(“华罗庚金杯”少年数学邀请赛试题)
12.试证方程[x]+[2x]+[4x]+[8x]+[16x]+[32x]=12345没有实数解.
(加拿大数学奥林匹克试题)
13.解下列方程、方程组.
(1)[3.8x]=[3.8]x+1 (x为自然数);
(“五羊杯”竞赛题)
(2)[2x+1]=x- ;
;
(重庆市竞赛题)
(3)求满足25{x}+[x]=125的所有x的和;
(青少年数学国际城市邀请赛试题)
(4)[2.018x]+[5.13y]=24(x,y都为自然数);
(北京市竞赛题)
(5)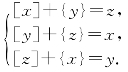
(奥地利数学竞赛题)
14.设r为实数,且![]() ,求[100r]的值.
,求[100r]的值.
(“希望杯”邀请赛试题)
(2)①+②+③,得2x+2y+2z=0.6,即
x+y+z=0.3, ④
④-①,得{y}+[z]=1.2,则{y}=0.2,[z]=1,
④-②,得{x}+[y]=0.1,则{x}=0.1,[y]=0,
④-③,得[x]+{z}=-1,则{z}=0,[x]=-1,
从而x=[x]+{x}=-0.9,y=[y]+{y}=0.2,z=[z]+{z}=1.
分别代入原方程,经讨论得原方程的解为x=![]()
12.假设方程有实数解x.
设x=[x]+r,0≤r<1.从而,nx=n[x]+nr,[nx]=n[x]+[nr].
式①与式②矛盾.所以,原方程没有实数解.
13.(1)x=2,原方程即为[3.8x]=3x+1.
(2)x=-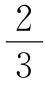 .
.
(3)2837 原方程可化为25x-24[x]=125.
(4)由5.13×5>24,得y=4,3,2,1,0,此时[5.13y]=5y,同理[2.018x]=2x,原方程变为2x+5y=24.得(x,y)=(2,4),(7,2),(12,0).
因为对任意的实数x,x=[x]+{x},于是,由方程①得[x]=[z],由方程②得[y]=[x],由方程③得[z]=[y].所以,[x]=[y]=[z]=n.同理可得{x}={y}={z}=r.因此,x=y=z=n+r.
因为对任取的x=y=z,可知x=[x]+{x}对方程组的每一个方程都成立.因此,满足方程组的所有实数组为{(t,t,t),t为实数}.
14.89-69=20,即已知等式的左侧为20项的和,
相关文章

,P2006的位置,求点P2006的横坐标.如图②,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3…......
2025-09-29

当n=106时,a=46;当n=107时,a为非整数,舍去.多元不等式通过确定主元、放缩、代入消元或运用不等式性质等方法,化多元不等式为一元不等式,是解多元不等式的重要策略.宋朝大学者朱熹曾说:“读书无疑者,须教有疑。”13.已知,求|x-1|-|x+3|的最大值和最小值.(北京市“迎春杯”竞赛题......
2025-09-29

解题思路对几种简单情形进行分析,然后从中归纳猜想出一般的规律.例2图中可数出的平行四边形的个数为().A.123B.114C.108D.105解题思路m×n长方形棋盘可数出长方形(1+2+…分析与解等腰直角三角形有怎样的几何特征?......
2025-09-29

分析与解题中28个字,“分”出现2次,“是”出现2次,“一”出现3次,其他字均各出现一次.28个自然数的平均数是23,其中有24个是连续的自然数.先想一个由二十多个连续自然数组成,并且平均数是23的具体例子.25个连续自然数11,12,13,…......
2025-09-29

在数学上,“包络”是指一系列的直线或曲线包围出另一个形状的情形,如左图中若干条直线组成了心脏线、抛物线.20世纪初,西方的数学书上讲述了用直线画曲线的各种画法,当时形成了“数学刺绣”的时尚.知能概述若把8个物体放入7个抽屉,则一定有一个抽屉放了2个或2个以上的物体;若把8个物体放入2个抽屉,则一定有一个抽屉放了4个或4个以上的物体;若把8个物体放入3个抽屉,则一定有一个抽屉放了3个或3个以上的物体......
2025-09-29

+|x-1997|的最小值.分析与解由于x具有任意性、无限性,所以通过逐个求出代数式的值来解题显然较难,不妨借助数轴,从绝对值的几何意义入手.从数轴上看,求|x-1|+|x-2|+|x-3|+…+|x-1997|的最小值,即在数轴上找出表示x的点,使它到表示数1,2,3,…+|x-an|值最小.质点运动运动与静止是哲学中的一对矛盾体,运动中蕴含了事物的相对静止,而在静止中又蕴含了事物的绝对运动.质点在数轴上运动,使点表示的有理数、线......
2025-09-29

璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西.”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意.知能概述图形有具体的,有抽象的;有平面的,有立体的.它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录.立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方......
2025-09-29

若能,请在图中标出来;若不能,请说明理由.3.方程组的解共有_________组.4.已知对任意的有理数a,b,关于x,y的二元一次方程(a-b)x-(a+b)y=a+b有一组公共解,则公共解为_________.5.已知有理数a,b,c,d,e,f满足方程组则f-e+d-c+b-a的值是_________.11.设a1,a2,…......
2025-09-29
相关推荐